خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
تابع (Function) چیست؟

تقریباً هر چیزی که در حسابان انجام می دهید به نحوی به توابع و نمودارهای آنها مرتبط است. حساب دیفرانسیل (Differential calculus) شامل یافتن شیب یا تندی توابع گوناگون، و حساب انتگرال (integral calculus) شامل محاسبۀ مساحت زیر توابع می باشد. و مفهوم تابع نه تنها برای حسابان حیاتی است، بلکه یکی از بنیادی ترین مفاهیم تمامی ریاضیات می باشد.

در واقع، یک تابع یک ارتباط بین دو چیز است که در آن مقدار عددی یک چیز به نحوی به مقدار دیگری بستگی دارد. مثالهایی در پیرامون ما وجود دارند: میانگین دمای روزانه در شهر شما، به زمان سال بستگی دارد یا تابعی از آن می باشد؛ مسافتی که یک شیء در حال سقوط طی کرده است، تابعی از اینست که از زمان رها کردن آن چقدر گذشته است؛ مساحت یک دایره تابعی از شعاع آن می باشد؛ و فشار گاز محصور شده در یک محفظه، تابعی از دمای آن می باشد.
شکل 1-5 را در نظر بگیرید.
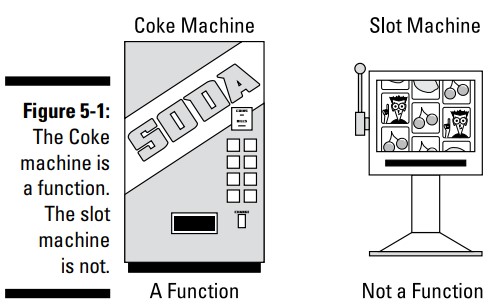
دستگاه فروش کوکا کولا یک تابع می باشد، زیرا بعد از اینکه ورودی ها (انتخابتان و پولتان) را به آن دادید، دقیقاً می دانید که خروجی چه خواهد بود. از سوی دیگر، در دستگاه اسلات (هر نوع دستگاه قمار که با سکه یا ژتون کار می کند و در کازینوها می باشد)، خروجی یک معما است، بنابراین یک تابع نمی باشد. به شکل 2-5 بنگرید.
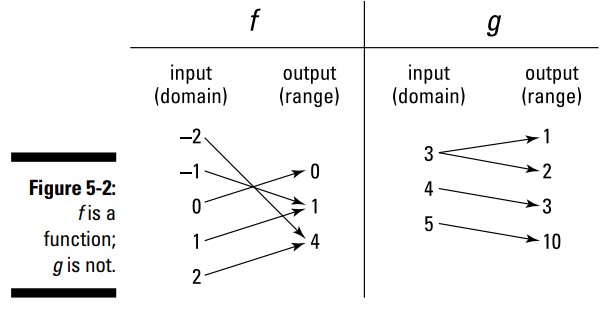
کارکرد مربع ساختن، \(f\)، یک تابع است، زیرا به ازاء هر ورودی دقیقاً یک خروجی دارد. اینکه هم \(2\) و هم \(-2\) خروجی یکسان \(4\) را تولید می کنند، مهم نیست، \(-2\) را در نظر بگیرید، در مورد خروجی آن هیچ معمایی وجود ندارد. با این وجود، هنگامی که \(3\) را به عنوان ورودی به \(g\) بدهید، نمی دانید که خروجی آن \(1\) یا \(2\) است. (فعلاً، در مورد اینکه چگونه قانون \(g\) این ورودی ها را به آن خروجی ها تبدیل می کند، نگران نباشید.) از آنجا که در توابع هیچ معمایی در مورد خروجی ها وجود ندارد، \(g\) یک تابع نمی باشد.
برخی افراد تمایل دارند تا به تابع به عنوان یک دستگاه فکر کنند. تابع مربع سازی \(f\) که در شکل 2-5 دیدید، را دوباره در نظر بگیرید. شکل 3-5 دو تا از این ورودی ها و خروجی های متناظر آنها را نشان می دهد.
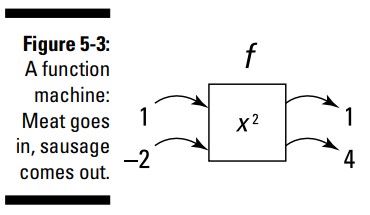
شما یک \(1\) را در این دستگاه تابع قرار می دهید و یک \(1\) از آن بیرون می آید؛ یک \(-2\) در آن قرار می دهید و یک \(4\) از آن بیرون می آید. یک دستگاه تابع یک ورودی را می گیرد، بر روی آن عملیاتی را به نحوی انجام می دهد، سپس خروجی را بیرون می اندازد.
گاهی اوقات وابستگی بین دو چیز اینگونه است که یکی علت و دیگری نتیجه است ـــ برای مثال، بالابردن دمای یک گاز منجر به بالا رفتن فشار آن می شود. در این مورد، دما متغیر مستقل و فشار متغیر وابسته می باشد، زیرا این فشار به آن دما بستگی دارد.
با این وجود، اغلب وابستگی اینگونه نیست که یکی علت و دیگری نتیجه باشد، بلکه صرفاً به نوعی ارتباطی بین آن دو چیز برقرار می باشد. با این حال، معمولاً متغیر مستقل چیزی است که هم اکنون می دانیم یا به سادگی می توانیم آن را مشخص سازیم، و متغیر وابسته چیزی است که می خواهیم آن را کشف کنیم. به عنوان مثال، شما نمی گویید که زمان علت افتادن یک شیء می باشد (جاذبه دلیل افتادن است)، اما اگر بدانید که از زمان رها کردن آن شیء چقدر می گذرد، می توانید اینکه چقدر سقوط کرده است را بدست آورید. بنابراین، زمان متغیر مستقل و مسافت سقوط، متغیر وابسته می باشد؛ و می توانید بگویید که این مسافت تابعی از زمان می باشد.
ارتباط بین این دو متغیر متناظر هر چه که باشد، متغیر وابسته (متغیر \(y\)) چیزی است که ما معمولاً بیشتر به آن علاقه داریم. به طور کلی، ما می خواهیم بدانیم همینطور که متغیر مستقل یا متغیر \(x\) به سمت راست می رود، برای متغیر وابسته یا متغیر \(y\) چه اتفاقی می افتد: اگر متغیر \(y\) (ارتفاع نمودار) بالا می رود یا پایین می آید، در اینصورت، چقدر تند است، یا اینکه آیا سطح نمودار مربوطه نه بالا می رود و نه پایین می آید؟
یک روش رایج برای نگارش تابع \(y=5x^3-2x^2+3\) اینست که \(y\) را با \(f(x)\) جایگزین کنید و آن را به شکل \(f(x)=5x^3-2x^2+3\) بنویسید. این صرفاً یک نماد متفاوت برای همان چیز است. این دو معادله، از هر نظر، به لحاظ ریاضی یکسان می باشند. دانش آموزان اغلب وقتیکه برای اولین بار این نماد را می بینند، متعجب می گردند. آنها با خودشان می اندیشند که این \(f\) چیست، و آیا \(f(x)\) به معنای \(f\) ضربدر \(x\) می باشد. اینطور نیست. اگر نماد تابع شما را به خطا می اندازد، توصیۀ من اینست که به \(f(x)\) به سادگی تمام، صرفاً به عنوان یک \(y\) که در زبانی دیگر نوشته شده است، فکر کنید. این \(f\) و این \(x\) را چیزهای جداگانه ای در نظر نگیرید؛ صرفاً به \(f(x)\) به نماد واحدی برای \(y\) بیندیشید.
شما همچنین می توانید به \(f(x)\) به منزلۀ خلاصه شده ای از "یک تابع از \(x\)" بیندیشید. شما می توانید بنویسید \(y=f(x)=3x^2\) ، که اینگونه تعبیر می شود "\(y\) تابعی از \(x\) ست و آن تابع برابر با \(3x^2\) می باشد." با این وجود، گاهی اوقات، حروف دیگری به جای \(f\) مورد استفاده قرار می گیرند ـــ مانند \(g(x)\) یا \(p(x)\) ـــ اغلب صرفاً به منظور تمایز قائل شدن بین توابع. حرف الفبای مورد استفاده برای نام تابع الزاماً نشان دهندۀ چیز خاصی نیست، اما گاهی اوقات از حرف آغازین یک کلمه استفاده می کنند (در آنصورت از یک حرف بزرگ الفبا استفاده می شود). به عنوان نمونه، شما می دانید که مساحت یک مربع با مربع ساختن طول یک ضلع آن بدست می آید: \(\text{Area} = \text{side}^2 \) یا \(A=s^2\). مساحت یک مربع، به طول ضلع آن بستگی دارد، یا تابعی از آن می باشد. با نماد تابع، شما می توانید آن را اینگونه بنویسید \(A(s)=s^2\) .
آزمون سریع: \(f(x)=x^2\) با تابع مساحت یک مربع، \(A(s)=s^2\) چه فرقی دارد؟
پاسخ: در \(f(x)=x^2\)، \(x\) می تواند هر عددی باشد، اما در \(A(s)=s^2\)، \(s\) باید عددی مثبت باشد، زیرا طول یک ضلع مربع نمی تواند برابر با صفر یا عددی منفی باشد. بنابراین این دو تابع به لحاظ دامنه هایشان متفاوتند.
دوباره تابع مربع ساختن \(y=x^2\) یا \(f(x)=x^2\) را در نظر بگیرید. هنگامی که \(3\) را به عنوان ورودی به این تابع بدهید، مقدار خروجی برابر با \(9\) خواهد بود. نماد تابع راحت است، زیرا شما می توانید به اختصاری این ورودی و خروجی را با نوشتن \(f(3)=9\) بیان کنید. یادتان باشد \(f(3)=9\) بدین معناست که هنگامی که \(x\) برابر با \(3\) باشد، \(f(x)\) برابر با \(9\) می شود؛ یا، معادلش، بیان می دارد که هرگاه که \(x\) برابر با \(3\) باشد، \(y\) برابر با \(9\) خواهد بود.
یک تابع مرکب (composite function) ترکیبی از دو تابع می باشد. به عنوان مثال، بهای تمام شدۀ انرژی الکتریکی مورد نیاز برای تهویۀ محل شما، به میزان برق مورد استفاده بستگی دارد، و میزان مصرف به دمای بیرون بستگی دارد.
از آنجا که هزینه به مصرف و مصرف به دما بستگی دارد، هزینه به دما نیز بستگی خواهد داشت. به زبان تابع، هزینه تابعی از مصرف است، مصرف تابعی از دما است، و از اینرو هزینه تابعی از دما است. این تابع آخر، یک ترکیب از دو تابع اول است، و یک تابع مرکب می باشد.
اجازه دهید \(f(x)=x^2\) و \(g(x)=5x-8\) باشد. \(3\) را وارد \(g(x)\) کنید: \(g(3)=5 \cdot 3 - 8 = 7\). اکنون این خروجی، \(7\)، را بگیرید، و آن را در \(f(x)\) جایگذاری کنید: \(f(7)=7^2=49\) . استعارۀ دستگاه نشان می دهد که من در اینجا چکار کرده ام. شکل 4-5 را ببینید. دستگاه \(g\)، \(3\) را به \(7\) تبدیل می کند، و سپس دستگاه \(f\)، \(7\) را به \(49\) تبدیل می کند.
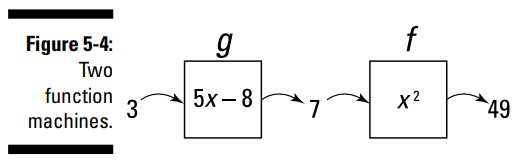
شما می توانید نتایج خالص این دو تابع را در یک مرحله با تابع مرکب زیر نشان دهید:
$$f(g(3))= 49$$
شما همیشه تابع درونی در یک تابع مرکب را ابتدا محاسبه می کنید: \(g(3)=7\). سپس آن خروجی، \(7\) ، را می گیرید، و \(f(7)\) را محاسبه می کنید، که برابر با \(49\) می باشد.
برای تعیین تابع مرکب کلی، \(f(g(x))\)، \(g(x)\) را در \(f(x)\) جایگذاری کنید، که برابر با \(5x-8\) می باشد. به عبارت دیگر، شما می خواهید \(f(5x-8)\) را تعیین کنید. تابع \(f\) یا دستگاه \(f\) یک ورودی را دریافت می کند و آن را مربع می سازد. از اینرو:
$$
f(5x-8)=(5x-8)^2 \\
=(5x-8)(5x-8) \\
= 25x^2-40x-40x+64 \\
= 25x^2-80x+64
$$
بنابراین:
$$f(g(x))=25x^2-80x+64$$

تابع چیست؟
در واقع، یک تابع یک ارتباط بین دو چیز است که در آن مقدار عددی یک چیز به نحوی به مقدار دیگری بستگی دارد. مثالهایی در پیرامون ما وجود دارند: میانگین دمای روزانه در شهر شما، به زمان سال بستگی دارد یا تابعی از آن می باشد؛ مسافتی که یک شیء در حال سقوط طی کرده است، تابعی از اینست که از زمان رها کردن آن چقدر گذشته است؛ مساحت یک دایره تابعی از شعاع آن می باشد؛ و فشار گاز محصور شده در یک محفظه، تابعی از دمای آن می باشد.
ویژگی های تعریف شدۀ یک تابع
یک تابع به ازاء هر ورودی (input) صرفاً یک خروجی (output) دارد.
شکل 1-5 را در نظر بگیرید.

دستگاه فروش کوکا کولا یک تابع می باشد، زیرا بعد از اینکه ورودی ها (انتخابتان و پولتان) را به آن دادید، دقیقاً می دانید که خروجی چه خواهد بود. از سوی دیگر، در دستگاه اسلات (هر نوع دستگاه قمار که با سکه یا ژتون کار می کند و در کازینوها می باشد)، خروجی یک معما است، بنابراین یک تابع نمی باشد. به شکل 2-5 بنگرید.

کارکرد مربع ساختن، \(f\)، یک تابع است، زیرا به ازاء هر ورودی دقیقاً یک خروجی دارد. اینکه هم \(2\) و هم \(-2\) خروجی یکسان \(4\) را تولید می کنند، مهم نیست، \(-2\) را در نظر بگیرید، در مورد خروجی آن هیچ معمایی وجود ندارد. با این وجود، هنگامی که \(3\) را به عنوان ورودی به \(g\) بدهید، نمی دانید که خروجی آن \(1\) یا \(2\) است. (فعلاً، در مورد اینکه چگونه قانون \(g\) این ورودی ها را به آن خروجی ها تبدیل می کند، نگران نباشید.) از آنجا که در توابع هیچ معمایی در مورد خروجی ها وجود ندارد، \(g\) یک تابع نمی باشد.
توابع خوب، برخلاف داستان ها و نوشته های ادبی خوب، دارای پایان قابل پیش بینی می باشند.
تعریف دامنه (domain) و بُرد (range): مجموعۀ تمامی ورودیهای یک تابع دامنۀ آن تابع نامیده می شود؛ مجموعۀ تمامی خروجی های یک تابع، برد آن تابع نامیده می شود.
برخی افراد تمایل دارند تا به تابع به عنوان یک دستگاه فکر کنند. تابع مربع سازی \(f\) که در شکل 2-5 دیدید، را دوباره در نظر بگیرید. شکل 3-5 دو تا از این ورودی ها و خروجی های متناظر آنها را نشان می دهد.

شما یک \(1\) را در این دستگاه تابع قرار می دهید و یک \(1\) از آن بیرون می آید؛ یک \(-2\) در آن قرار می دهید و یک \(4\) از آن بیرون می آید. یک دستگاه تابع یک ورودی را می گیرد، بر روی آن عملیاتی را به نحوی انجام می دهد، سپس خروجی را بیرون می اندازد.
متغیرهای مستقل و متغیرهای وابسته
تعریف متغیرهای مستقل (independent variable) و متغیرهای وابسته (dependent variable): در یک تابع، چیزهایی که وابسته به سایر چیزها هستند، متغیرهای وابسته نامیده می شوند؛ سایر چیزها، متغیرهای مستقل نامیده می شوند. از آنجا که شما اعداد را در متغیر مستقل جایگذاری می کنید، به آن متغیر ورودی (input variable) نیز گفته می شود. بعد از جایگذاری یک عدد، سپس خروجی یا پاسخ را برای آن متغیر مستقل محاسبه می کنید، بنابراین متغیر وابسته را متغیر خروجی (output variable) نیز می نامند. هنگامی که نمودار یک تابع را ترسیم می کنید، متغیر مستقل بر روی محور \(x\) امتداد می یابد، و متغیر وابسته بر روی محور \(y\) امتداد می یابد.
گاهی اوقات وابستگی بین دو چیز اینگونه است که یکی علت و دیگری نتیجه است ـــ برای مثال، بالابردن دمای یک گاز منجر به بالا رفتن فشار آن می شود. در این مورد، دما متغیر مستقل و فشار متغیر وابسته می باشد، زیرا این فشار به آن دما بستگی دارد.
با این وجود، اغلب وابستگی اینگونه نیست که یکی علت و دیگری نتیجه باشد، بلکه صرفاً به نوعی ارتباطی بین آن دو چیز برقرار می باشد. با این حال، معمولاً متغیر مستقل چیزی است که هم اکنون می دانیم یا به سادگی می توانیم آن را مشخص سازیم، و متغیر وابسته چیزی است که می خواهیم آن را کشف کنیم. به عنوان مثال، شما نمی گویید که زمان علت افتادن یک شیء می باشد (جاذبه دلیل افتادن است)، اما اگر بدانید که از زمان رها کردن آن شیء چقدر می گذرد، می توانید اینکه چقدر سقوط کرده است را بدست آورید. بنابراین، زمان متغیر مستقل و مسافت سقوط، متغیر وابسته می باشد؛ و می توانید بگویید که این مسافت تابعی از زمان می باشد.
ارتباط بین این دو متغیر متناظر هر چه که باشد، متغیر وابسته (متغیر \(y\)) چیزی است که ما معمولاً بیشتر به آن علاقه داریم. به طور کلی، ما می خواهیم بدانیم همینطور که متغیر مستقل یا متغیر \(x\) به سمت راست می رود، برای متغیر وابسته یا متغیر \(y\) چه اتفاقی می افتد: اگر متغیر \(y\) (ارتفاع نمودار) بالا می رود یا پایین می آید، در اینصورت، چقدر تند است، یا اینکه آیا سطح نمودار مربوطه نه بالا می رود و نه پایین می آید؟
نماد تابع (Function notation)
یک روش رایج برای نگارش تابع \(y=5x^3-2x^2+3\) اینست که \(y\) را با \(f(x)\) جایگزین کنید و آن را به شکل \(f(x)=5x^3-2x^2+3\) بنویسید. این صرفاً یک نماد متفاوت برای همان چیز است. این دو معادله، از هر نظر، به لحاظ ریاضی یکسان می باشند. دانش آموزان اغلب وقتیکه برای اولین بار این نماد را می بینند، متعجب می گردند. آنها با خودشان می اندیشند که این \(f\) چیست، و آیا \(f(x)\) به معنای \(f\) ضربدر \(x\) می باشد. اینطور نیست. اگر نماد تابع شما را به خطا می اندازد، توصیۀ من اینست که به \(f(x)\) به سادگی تمام، صرفاً به عنوان یک \(y\) که در زبانی دیگر نوشته شده است، فکر کنید. این \(f\) و این \(x\) را چیزهای جداگانه ای در نظر نگیرید؛ صرفاً به \(f(x)\) به نماد واحدی برای \(y\) بیندیشید.
یادداشت مترجم: \(f(x)\) را در فارسی به شکل "اِفِ ایکس" بخوانید. در انگلیسی آن را به شکل "f of x" می خوانند.
شما همچنین می توانید به \(f(x)\) به منزلۀ خلاصه شده ای از "یک تابع از \(x\)" بیندیشید. شما می توانید بنویسید \(y=f(x)=3x^2\) ، که اینگونه تعبیر می شود "\(y\) تابعی از \(x\) ست و آن تابع برابر با \(3x^2\) می باشد." با این وجود، گاهی اوقات، حروف دیگری به جای \(f\) مورد استفاده قرار می گیرند ـــ مانند \(g(x)\) یا \(p(x)\) ـــ اغلب صرفاً به منظور تمایز قائل شدن بین توابع. حرف الفبای مورد استفاده برای نام تابع الزاماً نشان دهندۀ چیز خاصی نیست، اما گاهی اوقات از حرف آغازین یک کلمه استفاده می کنند (در آنصورت از یک حرف بزرگ الفبا استفاده می شود). به عنوان نمونه، شما می دانید که مساحت یک مربع با مربع ساختن طول یک ضلع آن بدست می آید: \(\text{Area} = \text{side}^2 \) یا \(A=s^2\). مساحت یک مربع، به طول ضلع آن بستگی دارد، یا تابعی از آن می باشد. با نماد تابع، شما می توانید آن را اینگونه بنویسید \(A(s)=s^2\) .
آزمون سریع: \(f(x)=x^2\) با تابع مساحت یک مربع، \(A(s)=s^2\) چه فرقی دارد؟
پاسخ: در \(f(x)=x^2\)، \(x\) می تواند هر عددی باشد، اما در \(A(s)=s^2\)، \(s\) باید عددی مثبت باشد، زیرا طول یک ضلع مربع نمی تواند برابر با صفر یا عددی منفی باشد. بنابراین این دو تابع به لحاظ دامنه هایشان متفاوتند.
دوباره تابع مربع ساختن \(y=x^2\) یا \(f(x)=x^2\) را در نظر بگیرید. هنگامی که \(3\) را به عنوان ورودی به این تابع بدهید، مقدار خروجی برابر با \(9\) خواهد بود. نماد تابع راحت است، زیرا شما می توانید به اختصاری این ورودی و خروجی را با نوشتن \(f(3)=9\) بیان کنید. یادتان باشد \(f(3)=9\) بدین معناست که هنگامی که \(x\) برابر با \(3\) باشد، \(f(x)\) برابر با \(9\) می شود؛ یا، معادلش، بیان می دارد که هرگاه که \(x\) برابر با \(3\) باشد، \(y\) برابر با \(9\) خواهد بود.
توابع مرکب (Composite functions)
یک تابع مرکب (composite function) ترکیبی از دو تابع می باشد. به عنوان مثال، بهای تمام شدۀ انرژی الکتریکی مورد نیاز برای تهویۀ محل شما، به میزان برق مورد استفاده بستگی دارد، و میزان مصرف به دمای بیرون بستگی دارد.
از آنجا که هزینه به مصرف و مصرف به دما بستگی دارد، هزینه به دما نیز بستگی خواهد داشت. به زبان تابع، هزینه تابعی از مصرف است، مصرف تابعی از دما است، و از اینرو هزینه تابعی از دما است. این تابع آخر، یک ترکیب از دو تابع اول است، و یک تابع مرکب می باشد.
اجازه دهید \(f(x)=x^2\) و \(g(x)=5x-8\) باشد. \(3\) را وارد \(g(x)\) کنید: \(g(3)=5 \cdot 3 - 8 = 7\). اکنون این خروجی، \(7\)، را بگیرید، و آن را در \(f(x)\) جایگذاری کنید: \(f(7)=7^2=49\) . استعارۀ دستگاه نشان می دهد که من در اینجا چکار کرده ام. شکل 4-5 را ببینید. دستگاه \(g\)، \(3\) را به \(7\) تبدیل می کند، و سپس دستگاه \(f\)، \(7\) را به \(49\) تبدیل می کند.

شما می توانید نتایج خالص این دو تابع را در یک مرحله با تابع مرکب زیر نشان دهید:
$$f(g(3))= 49$$
شما همیشه تابع درونی در یک تابع مرکب را ابتدا محاسبه می کنید: \(g(3)=7\). سپس آن خروجی، \(7\) ، را می گیرید، و \(f(7)\) را محاسبه می کنید، که برابر با \(49\) می باشد.
برای تعیین تابع مرکب کلی، \(f(g(x))\)، \(g(x)\) را در \(f(x)\) جایگذاری کنید، که برابر با \(5x-8\) می باشد. به عبارت دیگر، شما می خواهید \(f(5x-8)\) را تعیین کنید. تابع \(f\) یا دستگاه \(f\) یک ورودی را دریافت می کند و آن را مربع می سازد. از اینرو:
$$
f(5x-8)=(5x-8)^2 \\
=(5x-8)(5x-8) \\
= 25x^2-40x-40x+64 \\
= 25x^2-80x+64
$$
بنابراین:
$$f(g(x))=25x^2-80x+64$$
در توابع مرکب، ترتیب حائز اهمیت است. به عنوان یک قاعدۀ کلی:
$$f(g(x)) \ne g(f(x))$$
$$f(g(x)) \ne g(f(x))$$
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: