خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
مشتق (Derivative)

در اینجا روش دیگری برای درک مفهوم یک مشتق داریم که حتی از مفهوم شیب بنیادی تر است: مشتق یک نرخ (rate) است. پس چرا من این فصل را با شیب آغاز کردم؟ زیرا شیب به برخی جهات ساده تر از این دو مفهوم است، و شیب مفهومی است که دوباره و دوباره در این کتاب و هر کتاب درسی حسابان دیگر، همچنان که به نمودار ده ها و ده ها تابع نگاه می کنید، به آن باز می گردید. اما قبل از اینکه به یک شیب برسید، به یک نرخ می رسید. یک شیب، به یک معنا، یک تصویر از یک نرخ است؛ نرخ در ابتدا می آید و تصویر آن بعد از آن می آید. درست مانند اینکه شما می توانید یک تابع داشته باشید، قبل از اینکه نمودارش را ببینید، شما می توانید یک نرخ داشته باشید، قبل از اینکه آن را به عنوان یک شیب ببینید.

لورل و هاردی را بر روی یک الاکلنگ تجسم کنید ـــ شکل 5-9 را بینید.
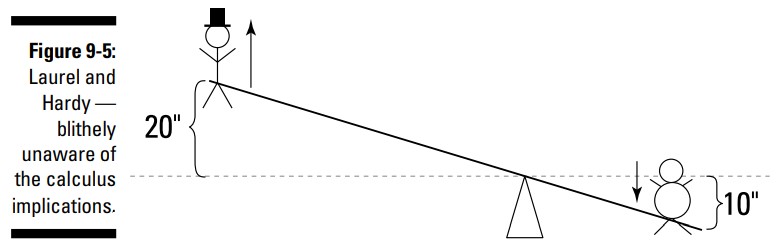
فرض بگیرید وزن هاردی دوبرابر وزن لورل است، برای اینکه تعادل بین آنها برقرار شود، هاردی باید نسبت به لورل دوبرابر به مرکز نزدیکتر بنشیند. و به ازاء هر اینچی که هاردی پایین می رود، لورل دو اینچ رو به بالا می رود. بنابراین لورل دوبرابر بیشتر از هاردی منتقل می شود. بفرمایید، شما یک مشتق بدست دارید!
لورل دوبرابر هاردی جابجا می شود، بنابراین با نمادهای حسابان شما این را اینگونه می نویسید:
$$dL=2dH$$
به زبان ساده تر، \(dL\) می تواند به عنوان تغییر در موقعیت لورل و \(dH\) می تواند به عنوان تغییر در موقعیت هاردی، مورد تفکر قرار گیرند. شما می توانید ببینید که اگر هاردی \(10\) اینچ پایین برود، سپس \(dH\) برابر با \(10\) خواهد بود، و از آنجا که \(dL\) برابر با \(2\) ضربدر \(dH\) می باشد، \(dL\) برابر با \(20\) خواهد بود ـــ بنابراین لورل \(20\) اینچ بالا می رود. تقسیم هر دو سمت این معادله بر روی \(dH\) نتیجۀ زیر را به شما می دهد:
$$\frac{dL}{dH}=2$$
و این مشتق لورل با توجه به هاردی می باشد. (این مشتق به شکل "دی ال، دی اچ" خوانده می شود، یا اینگونه خوانده می شود:"مشتق \(L\) با توجه به \(H\)".) این حقیقت که \(\frac{dL}{dH} = 2\) به سادگی به این معناست که لورل دوبرابر بیشتر از هاردی جابجا می شود. نرخ جابجایی لورل به ازاء هر اینچ جابجایی هاردی، برابر با \(2\) اینچ می باشد.
حالا بیایید از منظر دید هاردی به مسأله بنگریم. هاردی نصف لورل جابجا می شود، بنابراین شما همچنین می توانید بنویسید:
$$dH=\frac{1}{2}dL$$
تقسیم هر دو سمت معادله بر \(dL\) نتیجۀ زیر را به شما می دهد:
$$\frac{dH}{dL} = \frac{1}{2}$$
این مشتق هاردی با توجه به لورل می باشد، و بدین معناست که هاردی به ازاء هر اینچ جابجایی لورل، برابر \(\frac{1}{2}\) اینچ جابجا می گردد. بدین ترتیب، نرخ هاردی \(\frac{1}{2}\) اینچ به ازاء هر اینچ جابجایی لورل می باشد. راستی، شما همچنین می توانید این مشتق را با \(\frac{dL}{dH} = 2\)، که با \(\frac{dL}{dH}=\frac{2}{1}\) یکی است، بدست آورید، و آن را سروته کنید تا به \(\frac{dH}{dL}=\frac{1}{2}\) برسید.
این نرخ \(2\) اینچ به ازاء هر اینچ و \(\frac{1}{2}\) اینچ به ازاء هر اینچ، ممکن است اندکی عجیب به نظر آید، زیرا ما معمولاً به نرخها اینگونه فکر می کنیم که چیزی به ازاء هر واحد از زمان هستند، مانند مایل بر ساعت. اما یک نرخ می تواند هر چیزی به ازاء هر چیزی باشد. بنابراین هرگاه که این به ازاء هر آن (this per that) رسیدید، با یک نرخ مواجه شده اید؛ و اگر به یک نرخ رسیده اید، به یک مشتق رسیده اید.
در ارتباط با موضوع مایل بر ساعت (miles per hour) که اندکی پیش اشاره شد، فرض بگیرید که با سرعت ثابت \(60\) مایل بر ساعت مشغول رانندگی هستید. این نرخ (rate) خودرو شما است، و \(60\) مایل بر ساعت، مشتق موقعیت خودروی شما، \(p\) ، با توجه به زمان، \(t\) می باشد. با نمادهای حسابان، آن را اینگونه می نویسید:
$$\frac{dp}{dt} = 60 \frac{\text{miles}}{\text{hour}}$$
این به شما می گوید که موقعیت خودروی شما به ازاء هر ساعتی که زمان تغییر می کند، برابر \(60\) مایل تغییر می یابد. یا می توانید بگویید که موقعیت خودروی شما (در واحد مایل) \(60\) برابر بیشتر از تغییر زمان (در واحد ساعت) تغییر می کند. دوباره، مشتق صرفاً به شما می گوید که یک چیز در مقایسه با چیز دیگری، چقدر تغییر می کند.
و درست مانند مثال لورل و هاردی، این مشتق، همانند همۀ مشتق ها، می تواند سروته شود:
$$\frac{dt}{dp}=\frac{1}{60}=\frac{\text{hours}}{\text{mile}}$$
این نرخ ساعت بر مایل (hours-per-mile) مطمئناً از نرخ معمولی مایل بر ساعت، ناآشناتر است، اما با این اوصاف یک نرخ کاملاً قانونی است. این نرخ به شما می گوید که به ازاء هر مایلی که می روید، زمان به اندازۀ \(\frac{1}{60}\) ساعت، تغییر می کند. و به شما می گوید که این زمان (در واحد ساعت) به میزان \(\frac{1}{60}\) بیشتر از موقعیت خودرو (در واحد مایل) تغییر می کند.
نرخ ها (Rates) و شیب ها (slopes) یک ارتباط ساده دارند. تمامی نرخ های موجود در مثال های پیشین می توانند بر روی یک دستگاه مختصات \(\text{x-y}\) به صورت نمودار ترسیم شوند، که در آن هر نرخ به شکل یک شیب ظاهر گردد. مثال لورل و هاردی را دوباره در نظر بگیرید. لورل دوبرابر بیشتر از هاردی جابجا می شود. این می تواند با معادلۀ زیر نمایش داده شود:
$$L=2H$$
شکل 6-9 نمودار این تابع را نشان می دهد.
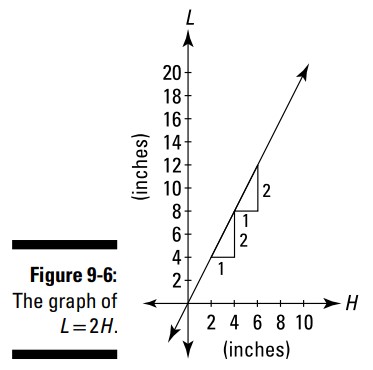
اینچ ها (inches) بر روی محور \(H\) نشان می دهند که هاردی از موقعیت آغازین الاکلنگ چقدر رو به بالا یا پایین جابجا شده است؛ اینچ ها بر روی محور \(L\) نشان می دهند که لورل چقدر رو به بالا یا پایین جابجا شده است. این خط به ازاء هر اینچی که به سمت راست می رود، \(2\) اینچ به سمت بالا می رود، و بدین ترتیب شیب آن برابر با \(\frac{2}{1}\) یا \(2\) می باشد. این نمایش بصری \(\frac{dL}{dH}=2\) می باشد، که نشان می دهد موقعیت لورل \(2\) برابر بیشتر از هاردی تغییر می کند.
یک تذکر دیگر. شما می دانید که \(\text{slope}=\frac{\text{rise}}{\text{run}}\) . خوب، شما می توانید به \(dL\) به عنوان rise و به \(dH\) به عنوان run فکر کنید. این همه چیز را کاملاً زیبا به یکدیگر گره می زند.
یادتان باشد که یک مشتق، صرفاً یک شیب است، و یک مشتق همچنین صرفاً یک نرخ است.

حسابان در زمین بازی
لورل و هاردی را بر روی یک الاکلنگ تجسم کنید ـــ شکل 5-9 را بینید.

فرض بگیرید وزن هاردی دوبرابر وزن لورل است، برای اینکه تعادل بین آنها برقرار شود، هاردی باید نسبت به لورل دوبرابر به مرکز نزدیکتر بنشیند. و به ازاء هر اینچی که هاردی پایین می رود، لورل دو اینچ رو به بالا می رود. بنابراین لورل دوبرابر بیشتر از هاردی منتقل می شود. بفرمایید، شما یک مشتق بدست دارید!
مشتق یک نرخ است. مشتق به سادگی اندازه گیری اینست که یک چیز در مقایسه با چیز دیگری، چقدر تغییر می کند ـــ و این یک نرخ است.
لورل دوبرابر هاردی جابجا می شود، بنابراین با نمادهای حسابان شما این را اینگونه می نویسید:
$$dL=2dH$$
به زبان ساده تر، \(dL\) می تواند به عنوان تغییر در موقعیت لورل و \(dH\) می تواند به عنوان تغییر در موقعیت هاردی، مورد تفکر قرار گیرند. شما می توانید ببینید که اگر هاردی \(10\) اینچ پایین برود، سپس \(dH\) برابر با \(10\) خواهد بود، و از آنجا که \(dL\) برابر با \(2\) ضربدر \(dH\) می باشد، \(dL\) برابر با \(20\) خواهد بود ـــ بنابراین لورل \(20\) اینچ بالا می رود. تقسیم هر دو سمت این معادله بر روی \(dH\) نتیجۀ زیر را به شما می دهد:
$$\frac{dL}{dH}=2$$
و این مشتق لورل با توجه به هاردی می باشد. (این مشتق به شکل "دی ال، دی اچ" خوانده می شود، یا اینگونه خوانده می شود:"مشتق \(L\) با توجه به \(H\)".) این حقیقت که \(\frac{dL}{dH} = 2\) به سادگی به این معناست که لورل دوبرابر بیشتر از هاردی جابجا می شود. نرخ جابجایی لورل به ازاء هر اینچ جابجایی هاردی، برابر با \(2\) اینچ می باشد.
یادداشت مترجم: عبارت \(\frac{dL}{dH}=2\) به زبان انگلیسی اینگونه خوانده می شود: "dee L, dee H"، همچنین اینگونه نیز خوانده می شود: "the derivative of L with respect to H" .
حالا بیایید از منظر دید هاردی به مسأله بنگریم. هاردی نصف لورل جابجا می شود، بنابراین شما همچنین می توانید بنویسید:
$$dH=\frac{1}{2}dL$$
تقسیم هر دو سمت معادله بر \(dL\) نتیجۀ زیر را به شما می دهد:
$$\frac{dH}{dL} = \frac{1}{2}$$
این مشتق هاردی با توجه به لورل می باشد، و بدین معناست که هاردی به ازاء هر اینچ جابجایی لورل، برابر \(\frac{1}{2}\) اینچ جابجا می گردد. بدین ترتیب، نرخ هاردی \(\frac{1}{2}\) اینچ به ازاء هر اینچ جابجایی لورل می باشد. راستی، شما همچنین می توانید این مشتق را با \(\frac{dL}{dH} = 2\)، که با \(\frac{dL}{dH}=\frac{2}{1}\) یکی است، بدست آورید، و آن را سروته کنید تا به \(\frac{dH}{dL}=\frac{1}{2}\) برسید.
این نرخ \(2\) اینچ به ازاء هر اینچ و \(\frac{1}{2}\) اینچ به ازاء هر اینچ، ممکن است اندکی عجیب به نظر آید، زیرا ما معمولاً به نرخها اینگونه فکر می کنیم که چیزی به ازاء هر واحد از زمان هستند، مانند مایل بر ساعت. اما یک نرخ می تواند هر چیزی به ازاء هر چیزی باشد. بنابراین هرگاه که این به ازاء هر آن (this per that) رسیدید، با یک نرخ مواجه شده اید؛ و اگر به یک نرخ رسیده اید، به یک مشتق رسیده اید.
سرعت ـــ آشناترین نرخ
در ارتباط با موضوع مایل بر ساعت (miles per hour) که اندکی پیش اشاره شد، فرض بگیرید که با سرعت ثابت \(60\) مایل بر ساعت مشغول رانندگی هستید. این نرخ (rate) خودرو شما است، و \(60\) مایل بر ساعت، مشتق موقعیت خودروی شما، \(p\) ، با توجه به زمان، \(t\) می باشد. با نمادهای حسابان، آن را اینگونه می نویسید:
$$\frac{dp}{dt} = 60 \frac{\text{miles}}{\text{hour}}$$
این به شما می گوید که موقعیت خودروی شما به ازاء هر ساعتی که زمان تغییر می کند، برابر \(60\) مایل تغییر می یابد. یا می توانید بگویید که موقعیت خودروی شما (در واحد مایل) \(60\) برابر بیشتر از تغییر زمان (در واحد ساعت) تغییر می کند. دوباره، مشتق صرفاً به شما می گوید که یک چیز در مقایسه با چیز دیگری، چقدر تغییر می کند.
و درست مانند مثال لورل و هاردی، این مشتق، همانند همۀ مشتق ها، می تواند سروته شود:
$$\frac{dt}{dp}=\frac{1}{60}=\frac{\text{hours}}{\text{mile}}$$
این نرخ ساعت بر مایل (hours-per-mile) مطمئناً از نرخ معمولی مایل بر ساعت، ناآشناتر است، اما با این اوصاف یک نرخ کاملاً قانونی است. این نرخ به شما می گوید که به ازاء هر مایلی که می روید، زمان به اندازۀ \(\frac{1}{60}\) ساعت، تغییر می کند. و به شما می گوید که این زمان (در واحد ساعت) به میزان \(\frac{1}{60}\) بیشتر از موقعیت خودرو (در واحد مایل) تغییر می کند.
برای نرخ های متفاوتی که شما می توانید ببینید، هیچ پایانی وجود ندارد. ما در اینجا مایل بر ساعت و ساعت بر مایل را دیدیم. نرخ هایی همچون مایل بر گالن (برای میزان بنزین مصرفی بر مایل)، گالن بر دقیقه (برای آبی که از یک استخر تخلیه می شود)، تولید به ازاء هر کارمند (برای بهره وری کارخانه)، و به همین ترتیب. نرخ ها می توانند ثابت یا در حال تغییر باشند. در هر دو مورد، هر نرخ یک مشتق است، و هر مشتق یک نرخ است.
ارتباط شیب-نرخ
نرخ ها (Rates) و شیب ها (slopes) یک ارتباط ساده دارند. تمامی نرخ های موجود در مثال های پیشین می توانند بر روی یک دستگاه مختصات \(\text{x-y}\) به صورت نمودار ترسیم شوند، که در آن هر نرخ به شکل یک شیب ظاهر گردد. مثال لورل و هاردی را دوباره در نظر بگیرید. لورل دوبرابر بیشتر از هاردی جابجا می شود. این می تواند با معادلۀ زیر نمایش داده شود:
$$L=2H$$
شکل 6-9 نمودار این تابع را نشان می دهد.

اینچ ها (inches) بر روی محور \(H\) نشان می دهند که هاردی از موقعیت آغازین الاکلنگ چقدر رو به بالا یا پایین جابجا شده است؛ اینچ ها بر روی محور \(L\) نشان می دهند که لورل چقدر رو به بالا یا پایین جابجا شده است. این خط به ازاء هر اینچی که به سمت راست می رود، \(2\) اینچ به سمت بالا می رود، و بدین ترتیب شیب آن برابر با \(\frac{2}{1}\) یا \(2\) می باشد. این نمایش بصری \(\frac{dL}{dH}=2\) می باشد، که نشان می دهد موقعیت لورل \(2\) برابر بیشتر از هاردی تغییر می کند.
یک تذکر دیگر. شما می دانید که \(\text{slope}=\frac{\text{rise}}{\text{run}}\) . خوب، شما می توانید به \(dL\) به عنوان rise و به \(dH\) به عنوان run فکر کنید. این همه چیز را کاملاً زیبا به یکدیگر گره می زند.
$$\text{slope}=\frac{\text{rise}}{\text{run}}=\frac{dL}{dH}=\text{rate}$$
یادتان باشد که یک مشتق، صرفاً یک شیب است، و یک مشتق همچنین صرفاً یک نرخ است.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: