خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
استفاده از مشتق برای درک شکل توابع

اگر فصل های 9 و 10 را خوانده باشید، احتمالاً در یافتن مشتق ها یک حرفه ای هستید. که چیزی خوبی است، زیرا در این فصل شما از مشتق ها برای درک شکل توابع استفاده می کنید ـــ کجا بالا می روند و کجا پایین می آیند، کجا به بیشینه ترین ارتفاع و کجا به کمینه ترین ارتفاع می رسند، چگونه انحناء می یابند، و به همین ترتیب. سپس در فصل 12 از دانشتان در مورد شکل توابع برای حل کردن مسأله های دنیای واقعی استفاده می کنید.

نمودار \(f(x)\) در شکل 1-11 را در نظر بگیرید.
تصور کنید در امتداد این تابع از چپ به راست رانندگی می کنید. در امتداد رانندگی تان، چندین نقطۀ جذاب بین \(a\) و \(l\) وجود دارد. تمامی آنها، به استثناء نقاط آغازین و پایانی، به تندی این جاده بستگی دارند ـــ به عبارت دیگر، شیب یا مشتق می باشند.
اکنون، خودتان را آماده کنید ـــ من قصد دارم تا جملات و تعاریف زیادی را، بصورت یکجا، به سمت شما پرتاب کنم. اگرچه، شما نباید با این مفاهیم مشکل زیادی داشته باشید زیرا اغلب آنها شامل ادراک عمومی مانند رانندگی رو به بالا و پایین یک شیب، یا بالا رفتن بسوی قلۀ یک تپه می باشند.
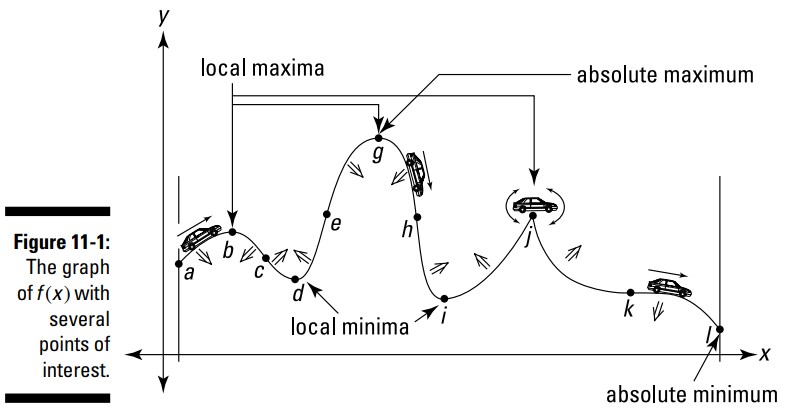
ابتدا توجه داشته باشید که همینطور که سفرتان را از \(a\) آغاز می کنید، بالا می روید. ازینرو این تابع افزایش می یابد و شیب آن و مشتق آن مثبت می باشد. شما این تپه را بالا می روید تا به \(b\) برسید که در آنجا جاده یکنواخت می شود. جاده در آنجا مسطح می شود، بنابراین شیب و مشتق برابر با صفر می گردند.
از آنجا که مشتق در \(b\) برابر با صفر می باشد، نقطۀ \(b\) یک نقطۀ سکون (stationary point) از این تابع نامیده می شود. همچنین نقطۀ \(b\) یک ماکزیمم موضعی (local maximum) یا ماکزیمم نسبی (relative maximum) از تابع \(f\) می باشد، زیرا آن بالای یک تپه است. برای اینکه \(b\) یک ماکزیمم موضعی باشد، کافیست نسبت به نقطه های مجاورش، بالاترین ارتفاع را داشته باشد. اینکه در تپۀ نزدیک آن نقطۀ \(g\) از آن بالاتر است، مهم نیست.
بعد از اینکه در نقطۀ \(a\) به قلۀ این تپه رسیدید، شروع به پایین رفتن می کنید ـــ اینکه مسلم است. بنابراین، بعد از \(b\) شیب و مشتق منفی می شوند، و این تابع کاهش می یابد. در سمت چپ هر ماکزیمم نسبی، شیب مثبت می باشد؛ در سمت راست یک ماکزیمم نسبی، شیب منفی می باشد.
نقطۀ قابل توجه بعدی \(c\) می باشد. آیا می توانید ببینید که همینطور که از \(b\) به \(c\) می روید، جاده تندتر و تندتر می شود، اما بعد از \(c\)، با وجود اینکه هنوز رو به پایین می روید، دوباره جاده تدریجاً شروع به انحنا یافتن می کند و تندی آن کاهش می یابد؟
آن فلش کوچک رو به پایین، بین \(b\) و \(c\)، در شکل 1-11 نشان می دهد که این بخش از جاده رو به سمت پایین انحنا می یابد ـــ گفته می شود این تابع در آنجا تقعر رو به پایین دارد. همانطور که می توانید ببینید، این جاده بین \(a\) و \(b\) نیز تقعر رو به پایین دارد.
هر جایی از یک تابع که تقعر رو به پایین داشته باشد، مشتق (و شیب) آن کاهش می یابد؛ هرجای یک تابع که تقعر رو به بالا داشته باشد، مشتق (و شیب) آن افزایش می یابد.
اوکی، پس این جاده تا \(c\) تقعر رو به پایین دارد که در آنجا به تقعر رو به بالا تغییر می کند. از آنجا که تقعر در \(c\) تغییر می کند، آن یک نقطۀ عطف (point of inflection) می باشد. نقطۀ \(c\) همچنین تندترین نقطه در این بخش از جاده می باشد. نقاط عطف همیشه در تندترین ـــ یا دارای کمترین تندی ـــ نسبت به نقاط مجاورشان می باشند.
بیایید به رانندگی شما بازگردیم. بعد از نقطۀ \(c\)، شما به پایین رفتن ادامه می دهید تا اینکه به نقطۀ \(d\) برسید، ته دره. نقطۀ \(d\)، نقطۀ سکون (stationary point) دیگری می باشد، زیرا جاده در آنجا مسطح می شود و مشتق برابر با صفر می گردد. همچنین نقطۀ \(d\) یک مینیم موضعی یا مینیمم نسبی می باشد زیرا پایین ترین نقطه نسبت به نقطه های همجوارش می باشد.
بعد از \(d\)، رو به بالا سفر می کنید، و از \(e\)، که نقطۀ عطف (inflection point) دیگری می باشد، عبور می کنید. این تندترین نقطۀ بین \(d\) و \(g\) می باشد و نقطه ای است که بزرگترین مشتق در آن است. شما در چشم انداز زیبای \(g\) توقف می کنید، \(g\) نقطۀ سکون و ماکزیمم موضعی دیگری می باشد. همچنین نقطۀ \(g\) ماکزیمم مطلق در بازۀ \(a\) تا \(l\) می باشد زیرا بالاترین نقطه در این جاده از \(a\) تا \(l\) می باشد.
با پایین رفتن از \(g\)، از نقطۀ عطف دیگری، \(h\)، و مینیمم موضعی دیگری، \(i\)، عبور می کنید، سپس رو به بالا به \(j\) می روید که شما به شکل احمقانه ای بر روی قله رانندگی می کنید. چرخهای جلوی شما از آن عبور می کنند اما شاسی ماشین شما در نوک پرتگاه گیر می کند، ماشین شما مانند یک الاکلنگ شروع به حرکت می کند و در این وضعیت چرخها هم در هوا در چرخشند. دلیل این حرکت الاکلنگی ماشین شما در \(j\) اینست که شما نمی توانید یک خط مماس در آنجا ترسیم کنید. عدم وجود خط مماس یعنی شیبی هم وجود ندارد؛ و عدم وجود شیب یعنی مشتقی هم وجود ندارد، یا می توانید بگویید که مشتق در \(j\) تعریف نشده (undefined) می باشد. یک نقطۀ برگشت نوک تیز همانند \(j\) گوشه (corner) نامیده می شود. (راستی، در مورد عبارت بدون شیب و بدون مشتق مراقب باشید. در این دو مورد عدم وجود به معنای صفر بودن شیب یا مشتق نمی باشد، بلکه مشتق اساساً وجود ندارد.)
بعد از اینکه با زور ماشین را از آن وضعیت الاکلنگی نجات دادید، بسوی پایین می روید، تندی این جاده کمتر و کمتر می شود تا اینکه در \(k\) مسطح می گردد. (مجدداً توجه داشته باشید از آنجایی که این شیب و این مشتق در مسیر \(k\) اعداد منفی کوچکتر و کوچکتری می شوند، در واقع آنها افزایش می یابند.) نقطۀ \(k\) نقطۀ سکون دیگری می باشد، زیرا مشتق آن برابر با صفر است. همچنین نقطۀ عطف دیگری نیز می باشد زیرا تقعر در \(k\) از بالا به پایین تعویض می شود. بعد از گذشتن از \(k\)، بسوی پایین و \(l\) می روید، که مقصد نهایی شما می باشد. از آنجا که \(l\) نقطۀ پایانی (endpoint) این بازه می باشد، یک مینیم موضعی نمی باشد ـــ نقاط پایانی هرگز به عنوان ماکزیمم یا مینیمم موضعی توصیف نمی شوند ـــ اما مینیمم مطلق (absolute minimum) در این بازه می باشد زیرا پایین ترین نقطه از \(a\) تا \(l\) می باشد.
امیدوارم از این سفر لذت برده باشید.
در اینجا می خواهم سفر شما و برخی از اصطلاحات و تعاریف گفته شده را مرور کنم و در عین حال چند اصطلاح بیشتر را به شما معرفی کنم:

یک سفر جاده ای با حسابان
نمودار \(f(x)\) در شکل 1-11 را در نظر بگیرید.
تصور کنید در امتداد این تابع از چپ به راست رانندگی می کنید. در امتداد رانندگی تان، چندین نقطۀ جذاب بین \(a\) و \(l\) وجود دارد. تمامی آنها، به استثناء نقاط آغازین و پایانی، به تندی این جاده بستگی دارند ـــ به عبارت دیگر، شیب یا مشتق می باشند.
اکنون، خودتان را آماده کنید ـــ من قصد دارم تا جملات و تعاریف زیادی را، بصورت یکجا، به سمت شما پرتاب کنم. اگرچه، شما نباید با این مفاهیم مشکل زیادی داشته باشید زیرا اغلب آنها شامل ادراک عمومی مانند رانندگی رو به بالا و پایین یک شیب، یا بالا رفتن بسوی قلۀ یک تپه می باشند.

شیب های مثبت و منفی (Positive and negative slopes)
ابتدا توجه داشته باشید که همینطور که سفرتان را از \(a\) آغاز می کنید، بالا می روید. ازینرو این تابع افزایش می یابد و شیب آن و مشتق آن مثبت می باشد. شما این تپه را بالا می روید تا به \(b\) برسید که در آنجا جاده یکنواخت می شود. جاده در آنجا مسطح می شود، بنابراین شیب و مشتق برابر با صفر می گردند.
از آنجا که مشتق در \(b\) برابر با صفر می باشد، نقطۀ \(b\) یک نقطۀ سکون (stationary point) از این تابع نامیده می شود. همچنین نقطۀ \(b\) یک ماکزیمم موضعی (local maximum) یا ماکزیمم نسبی (relative maximum) از تابع \(f\) می باشد، زیرا آن بالای یک تپه است. برای اینکه \(b\) یک ماکزیمم موضعی باشد، کافیست نسبت به نقطه های مجاورش، بالاترین ارتفاع را داشته باشد. اینکه در تپۀ نزدیک آن نقطۀ \(g\) از آن بالاتر است، مهم نیست.
بعد از اینکه در نقطۀ \(a\) به قلۀ این تپه رسیدید، شروع به پایین رفتن می کنید ـــ اینکه مسلم است. بنابراین، بعد از \(b\) شیب و مشتق منفی می شوند، و این تابع کاهش می یابد. در سمت چپ هر ماکزیمم نسبی، شیب مثبت می باشد؛ در سمت راست یک ماکزیمم نسبی، شیب منفی می باشد.
نقاط تقعر (Concavity) و عطف (inflection)
نقطۀ قابل توجه بعدی \(c\) می باشد. آیا می توانید ببینید که همینطور که از \(b\) به \(c\) می روید، جاده تندتر و تندتر می شود، اما بعد از \(c\)، با وجود اینکه هنوز رو به پایین می روید، دوباره جاده تدریجاً شروع به انحنا یافتن می کند و تندی آن کاهش می یابد؟
آن فلش کوچک رو به پایین، بین \(b\) و \(c\)، در شکل 1-11 نشان می دهد که این بخش از جاده رو به سمت پایین انحنا می یابد ـــ گفته می شود این تابع در آنجا تقعر رو به پایین دارد. همانطور که می توانید ببینید، این جاده بین \(a\) و \(b\) نیز تقعر رو به پایین دارد.
یادآور در مورد تقعر: تقعر رو به پایین شبیه یک اخم است، تقعر رو به بالا شبیه یک فنجان است. بخشی از یک تابع که تقعر رو به پایین دارد شبیه یک اخم است. و جاییکه تقعر رو به بالا دارد، مانند بین \(c\) و \(e\)، شبیه یک فنجان است.
هر جایی از یک تابع که تقعر رو به پایین داشته باشد، مشتق (و شیب) آن کاهش می یابد؛ هرجای یک تابع که تقعر رو به بالا داشته باشد، مشتق (و شیب) آن افزایش می یابد.
اوکی، پس این جاده تا \(c\) تقعر رو به پایین دارد که در آنجا به تقعر رو به بالا تغییر می کند. از آنجا که تقعر در \(c\) تغییر می کند، آن یک نقطۀ عطف (point of inflection) می باشد. نقطۀ \(c\) همچنین تندترین نقطه در این بخش از جاده می باشد. نقاط عطف همیشه در تندترین ـــ یا دارای کمترین تندی ـــ نسبت به نقاط مجاورشان می باشند.
در مورد بخش هایی از تابع که دارای شیب منفی می باشد، مراقب باشید. نقطۀ \(c\) تندترین نقطه در بین نقاط مجاورش می باشد زیرا نسبت به هر نقطۀ دیگری در نزدیکی آن دارای شیب منفی بزرگتری می باشد. اما یادتان باشد که یک عدد منفی بزرگ، در واقع یک عدد کوچک است، بنابراین شیب و مشتق در \(c\) در واقع کوچکترین نسبت به همۀ نقاط مجاورش می باشد. از \(b\) تا \(c\) مشتق این تابع کاهش می یابد (زیرا یک عدد منفی بزرگتر می شود). از \(c\) تا \(d\) مشتق افزایش می یابد (زیرا یک عدد منفی کوچکتر می شود). متوجه شدید؟
مینیمم موضعی (local minimum)
بیایید به رانندگی شما بازگردیم. بعد از نقطۀ \(c\)، شما به پایین رفتن ادامه می دهید تا اینکه به نقطۀ \(d\) برسید، ته دره. نقطۀ \(d\)، نقطۀ سکون (stationary point) دیگری می باشد، زیرا جاده در آنجا مسطح می شود و مشتق برابر با صفر می گردد. همچنین نقطۀ \(d\) یک مینیم موضعی یا مینیمم نسبی می باشد زیرا پایین ترین نقطه نسبت به نقطه های همجوارش می باشد.
ماکزیمم مطلق (absolute maximum)
بعد از \(d\)، رو به بالا سفر می کنید، و از \(e\)، که نقطۀ عطف (inflection point) دیگری می باشد، عبور می کنید. این تندترین نقطۀ بین \(d\) و \(g\) می باشد و نقطه ای است که بزرگترین مشتق در آن است. شما در چشم انداز زیبای \(g\) توقف می کنید، \(g\) نقطۀ سکون و ماکزیمم موضعی دیگری می باشد. همچنین نقطۀ \(g\) ماکزیمم مطلق در بازۀ \(a\) تا \(l\) می باشد زیرا بالاترین نقطه در این جاده از \(a\) تا \(l\) می باشد.
مشکل خودرو: الاکلنگ بر روی گوشه
با پایین رفتن از \(g\)، از نقطۀ عطف دیگری، \(h\)، و مینیمم موضعی دیگری، \(i\)، عبور می کنید، سپس رو به بالا به \(j\) می روید که شما به شکل احمقانه ای بر روی قله رانندگی می کنید. چرخهای جلوی شما از آن عبور می کنند اما شاسی ماشین شما در نوک پرتگاه گیر می کند، ماشین شما مانند یک الاکلنگ شروع به حرکت می کند و در این وضعیت چرخها هم در هوا در چرخشند. دلیل این حرکت الاکلنگی ماشین شما در \(j\) اینست که شما نمی توانید یک خط مماس در آنجا ترسیم کنید. عدم وجود خط مماس یعنی شیبی هم وجود ندارد؛ و عدم وجود شیب یعنی مشتقی هم وجود ندارد، یا می توانید بگویید که مشتق در \(j\) تعریف نشده (undefined) می باشد. یک نقطۀ برگشت نوک تیز همانند \(j\) گوشه (corner) نامیده می شود. (راستی، در مورد عبارت بدون شیب و بدون مشتق مراقب باشید. در این دو مورد عدم وجود به معنای صفر بودن شیب یا مشتق نمی باشد، بلکه مشتق اساساً وجود ندارد.)
افتادن در سرازیری
بعد از اینکه با زور ماشین را از آن وضعیت الاکلنگی نجات دادید، بسوی پایین می روید، تندی این جاده کمتر و کمتر می شود تا اینکه در \(k\) مسطح می گردد. (مجدداً توجه داشته باشید از آنجایی که این شیب و این مشتق در مسیر \(k\) اعداد منفی کوچکتر و کوچکتری می شوند، در واقع آنها افزایش می یابند.) نقطۀ \(k\) نقطۀ سکون دیگری می باشد، زیرا مشتق آن برابر با صفر است. همچنین نقطۀ عطف دیگری نیز می باشد زیرا تقعر در \(k\) از بالا به پایین تعویض می شود. بعد از گذشتن از \(k\)، بسوی پایین و \(l\) می روید، که مقصد نهایی شما می باشد. از آنجا که \(l\) نقطۀ پایانی (endpoint) این بازه می باشد، یک مینیم موضعی نمی باشد ـــ نقاط پایانی هرگز به عنوان ماکزیمم یا مینیمم موضعی توصیف نمی شوند ـــ اما مینیمم مطلق (absolute minimum) در این بازه می باشد زیرا پایین ترین نقطه از \(a\) تا \(l\) می باشد.
امیدوارم از این سفر لذت برده باشید.
خاطرات این سفر
در اینجا می خواهم سفر شما و برخی از اصطلاحات و تعاریف گفته شده را مرور کنم و در عین حال چند اصطلاح بیشتر را به شما معرفی کنم:
-
تابع \(f\) در شکل 1-11 در نقاط سکون (stationary points) یا نقاط هم سطح (level points) که نقاط \(b\)، \(d\)، \(g\)، \(i\)، و \(k\) می باشند، دارای مشتق صفر می باشد. در \(j\) مشتق تعریف نشده (undefined) می باشد. این نقاط که در آنها مشتق یا صفر یا تعریف نشده می باشد نقاط بحرانی (critical points) این تابع می باشند. مقادیر \(x\) این نقاط بحرانی، اعداد بحرانی (critical numbers) این تابع نامیده می شوند. (توجه داشته باشید که اعداد بحرانی باید در دامنۀ تابع باشند.)
-
تمامی ماکزیمم ها و مینیمم های موضعی ـــ قله ها و دره ها ـــ باید در نقاط بحرانی رخ دهند. با این حال، الزاماً تمامی نقاط بحرانی، ماکزیمم یا مینیمم موضعی نیستند. به عنوان مثال، نقطۀ \(k\)، یک نقطۀ بحرانی است، اما نه ماکزیمم موضعی و نه مینیمم موضعی است. ماکزیمم ها و مینیمم های موضعی مجتمعاً، اکسترمم های موضعی (local extrema) آن تابع نامیده می شوند. اگر می خواهید شبیه یک پروفسور به نظر برسید، بسیاری از این اصطلاحات را باید یاد بگیرید. یک ماکزیمم یا مینیمم موضعی واحد، یک اکسترمم موضعی (local extremum) نامیده می شود. ماکزیمم مطلق (absolute max) بالاترین نقطه در مسیر \(a\) به \(l\) می باشد. مینیمم مطلق (absolute min) پایین ترین نقطه می باشد.
یادداشت مترجم: کلمۀ maximum به معنای ماکزیمم (بیشینه، حداکثر) در شکل جمع آن به دو صورت maximums و maxima نوشته می شود که این شکل دوم در ریاضی رایجتر است. همچنین کلمۀ minimum (مینیمم، کمینه) نیز در شکل جمع آن به دو صورت minimums و minima نوشته می شود. همچنین کلمۀ extremum (اکسترمم) نیز در حالت جمعش به شکل extrema رایج است.
-
هرگاه که شما رو به سمت بالا می روید، که در آنجا مشتق مثبت است، این تابع افزایش می یابد؛ هرگاه که رو به پایین می روید، که در آنجا مشتق منفی است، تابع کاهش می یابد. همچنین این تابع در نقطۀ \(k\) ، که یک نقطۀ عطف افقی می باشد، کاهش می یابد، حتی با وجود اینکه شیب و مشتق در آنجا صفر می باشند. من درک می کنم که این اندکی عجیب به نظر آید، اما اینگونه کار می کند ـــ حرف من را در این باره بپذیرید. در تمامی نقاط عطف افقی (horizontal inflection points) یک تابع یا افزایش می یابد و یا کاهش. در اکسترمم های موضعی (local extrema) \(b\)، \(d\)، \(g\)، \(i\)، و \(j\)، این تابع نه افزایش می یابد و نه کاهش.
-
این تابع هرگاه که به شکل یک فنجان یا لبخند (بعضی اعتقاد دارند لبخند هم صحیح است) باشد، تقعر رو به بالا دارد، و هرگاه که شبیه یک اخم باشد، تقعر رو به پایین دارد. نقاط عطف (Inflection points) \(c\)، \(e\)، \(h\)، و \(k\) محل هایی هستند که تقعر در آنها از بالا به پایین یا برعکس تغییر می کند. همچنین نقاط عطف، تندترین یا دارای کمترین شیب، در بین نقاط همجوارشان می باشند.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (1 دیدگاه)
دیدگاه خود را ثبت کنید: