ماکزیمم مطلق (absolute max) و مینیمم مطلق (absolute min) یک تابع در سراسر دامنۀ آن، بالاترین و پایینترین مقادیر آن تابع (ارتفاع ها) در هر جایی که آن تابع تعریف شده باشد، می باشند. برخلاف بخش پیشین که شما دیدید که یک تابع پیوسته باید هم ماکزیمم مطلق و هم مینیمم مطلق را در یک بازۀ بسته (closed interval) داشته باشد، هنگامی که کل دامنۀ یک تابع را لحاظ می کنید، یک تابع می تواند ماکزیمم مطلق، مینیمم مطلق، یا هر دوی آنها را داشته باشد، همچنین می تواند هیچکدام را نداشته باشد. به عنوان مثال، سهمی (شلجمی) \(y=x^2\) در نقطۀ \((0,0)\) دارای یک مینیمم مطلق می باشد ـــ پایین شکل فنجان ـــ اما هیچ ماکزیمم مطلقی ندارد، زیرا این تابع تا ابد به سمت راست و چپ رو بسوی بالا می رود. شما ممکن است با خودتان فکر کنید که ماکزیمم مطلق آن بی نهایت (infinity) است، اما بی نهایت یک عدد نمی باشد، و از این رو نمی تواند به عنوان یک ماکزیمم واجد شرایط شناخته شود (ایضاً شما نمی توانید از منفی بی نهایت به عنوان یک مینیمم مطلق استفاده کنید).





مفهوم بالاترین نقطه و پایین ترین نقطۀ یک تابع، به جهتی بسیار ساده به نظر می رسد، اینطور نیست؟ اما در عمل یک پیچیدگی وجود دارد. این پیچیدگی دسته ای از چیزها می باشد که به عنوان ماکزیمم ها و مینیمم ها واجد شرایط شناخته نمی شوند.

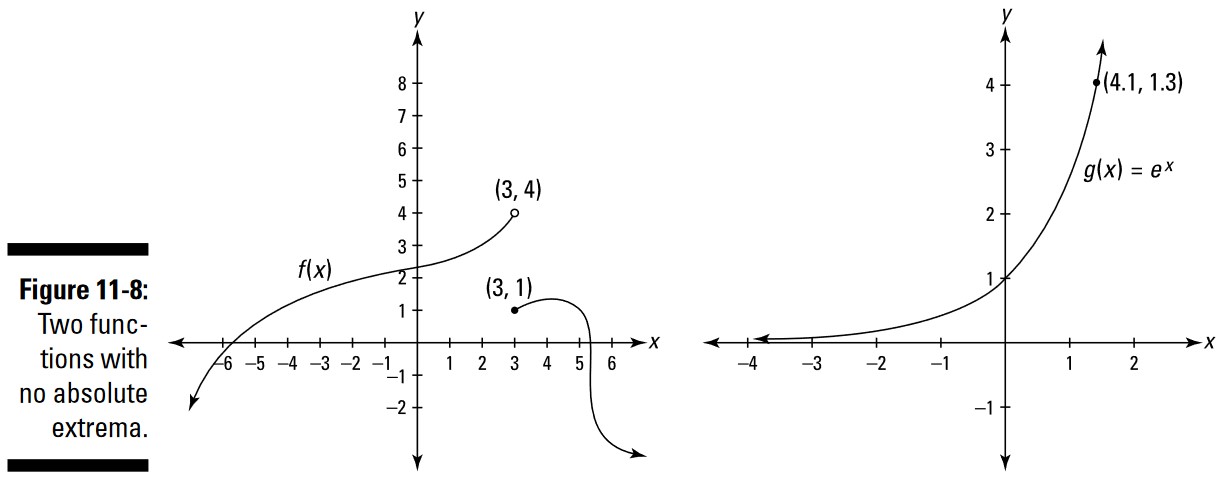
من قبلاً اشاره کردم که بی نهایت و منفی بی نهایت واجد شرایط نمی باشند. سپس نقاط پایانی خالی مانند \((3,4)\) در \(f(x)\) در شکل 8-11 هستند. \(f(x)\) یک ماکزیمم مطلق ندارد. ماکزیمم آن \(4\) نیست، زیرا آن هرگز به \(4\) نمی رسد، و ماکزیمم آن نمی تواند چیزی کمتر از \(4\) باشد، مانند \(3.999\)، زیرا از آن بالاتر می رود. به طرز مشابهی، یک حفرۀ بی نهایت کوچک در یک تابع نمی تواند به عنوان یک ماکزیمم یا مینیمم واجد شرایط باشد. به عنوان مثال، تابع قدر مطلق \(y=|x|\) ، تابعی \(V\) شکل با یک گوشۀ نوک تیز در مبدأ مختصات؛ اگر نمی توانید آن را تجسم کنید، به تابع \(g\) در شکل 8-7 بازگردید. \(y=|x|\) ماکزیمم مطلق ندارد، زیرا تا بی نهایت بالا می رود. مینیمم مطلق آن در \((0,0)\) می باشد. اما فعلاً، فرض کنید شما با بیرون کشیدن نقطۀ \((0,0)\) و رها کردن یک حفرۀ بی نهایت کوچک در آنجا، این تابع را اندکی تغییر داده اید. اکنون این تابع هیچ مینیمم مطلقی ندارد.

اکنون \(g(x)\) را در شکل 8-11 در نظر بگیرید. آن نوع دیگری از این وضعیت را نشان می دهد که به عنوان ماکزیمم یا مینیمم مطلق، واجد شرایط نمی باشد. \(g(x)\) مینیمم مطلقی ندارد. با رفتن به سمت چپ، \(g\) در امتداد خط مجانب افقی \(y=0\) می خزد، همیشه کمتر و کمتر می شود، اما هرگز به اندازۀ صفر کم نمی شود. از آنجایی که هرگز به صفر نمی رسد، صفر نمی تواند مینیمم مطلق باشد، و در آنجا مینیمم مطلق دیگری نمی تواند وجود داشته باشد (فرض کنید \(0.0001\)) زیرا در نقطه ای در سمت چپ آن، \(g\) از هر عدد کوچکی که بتوانید آن را نامگذاری کنید، کوچکتر می شود.

با در نظر گرفتن مطالب بالا، در اینجا یک رویکرد گام به گام برای یافتن ماکزیمم و مینیمم مطلق یک تابع را می بینید (اگر ماکزیمم یا مینیممی داشته باشد):

1. ارتفاع آن تابع را در هر کدام از اعداد بحرانی اش بیابید. (بیاد بیاورید که اعداد بحرانی یک تابع، مقادیر \(x\) درون دامنۀ آن تابع می باشند که در آن مشتق برابر با صفر یا تعریف نشده باشد.)
   شما این کار را در بخش قبلی انجام دادید، اما این بار شما تمامی اعداد بحرانی را مدنظر قرار می دهید، و نه فقط آنهایی را که در یک بازۀ معین باشند. بالاترین این مقادیر، ماکزیمم مطلق آن تابع خواهد بود مگر اینکه آن تابع از آن نقطه بالاتر برود که در آن صورت تابع مربوطه ماکزیمم مطلق نخواهد داشت. پایینترین این مقادیر، مینییمم مطلق آن تابع خواهد بود مگر اینکه آن تابع از آن نقطه پایینتر برود که در آن صورت تابع مربوطه مینیمم مطلق نخواهد داشت. گام های 2 و 3 به شما کمک می کنند کشف کنید که آیا آن تابع از آن بالاترین نقطۀ بحرانی، بالاتر می رود و یا اینکه از پایینترین نقطۀ بحرانی پایینتر می رود. اگر گام 1 را بر روی \(g(x)\) در شکل 8-11 اعمال کنید، درخواهید یافت که هیچ نقطۀ بحرانی ندارد. هنگامی که این اتفاق رخ دهد، کار تمام است. آن تابع نه ماکزیمم مطلق و نه مینیمم مطلق خواهد داشت.
   
   
2. بررسی کنید که آیا این تابع تا بی نهایت بالا می رود یا تا منفی بی نهایت پایین می آید.
   اگر تابعی تا مثبت بی نهایت بالا رود یا تا منفی بی نهایت پایین رود، اگر چنین چیزی در منتهی الیه سمت راست یا سمت چپ یا در یک خط مجانب عمودی رخ دهد. بنابراین، \(\lim \limits_{x \to \infty} f(x)\) و \(\lim \limits_{x \to -\infty} f(x)\) را ارزیابی کنید ـــ به این به اصطلاح رفتار پایانی (end behavior) آن تابع می گویند ـــ و حد آن تابع همچنانکه \(x\) به هر کدام از خط های مجانب عمودی از چپ و از راست نزدیک می شود (اگر خط مجانبی باشد). اگر آن تابع تا مثبت بی نهایت بالا رود، ماکزیمم مطلقی نخواهد داشت؛ اگر تا منفی بی نهایت پایین بیاید، مینیمم مطلقی نخواهد داشت.
   
   
3. نمودار تابع را بکشید تا خطهای مجانب افقی و ویژگی های عجیبی همچون ناپیوستگی جهشی (jump discontinuity) را در \(f(x)\) در شکل 8-11 بررسی کنید.
   به نمودار این تابع بنگرید. اگر می بینید که این تابع از بالاترین عدد بحرانی اش بالاتر می رود، ماکزیمم مطلق ندارد؛ اگر از پایین ترین عدد بحرانی اش، پایینتر بیاید، مینیمم مطلق ندارد. این فرآیند سه مرحله ای را بر روی \(f(x)\) در شکل 8-11 بکار بگیرید، گام 1 این دو نقطۀ بحرانی را آشکار خواهد ساخت: نقطۀ پایانی در \((3,1)\) و مینیمم موضعی تقریباً در \((4.1,1.3)\). در گام 2 درخواهید یافت که \(f\) تا منفی بی نهایت پایین می رود و از این رو مینیمم مطلق ندارد. در نهایت، در گام 3، خواهید دید که \(f\) از بالاترین نقاط بحرانی، \((4.1,1.3)\)، بالاتر می رود، و بنابراین ماکزیمم مطلق ندارد. کار تمام است!