یافتن مکان تقعر و نقاط عطف

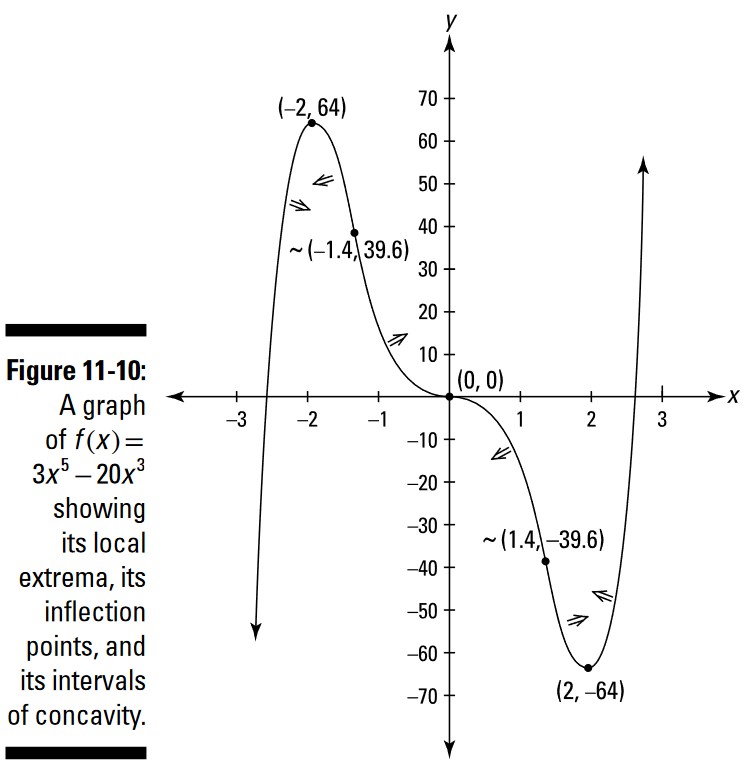
به شکل 2-11 بازگردید و تابع $f(x)=3x^5-20x^3$ را دوباره ببینید. شما از سه عدد بحرانی $f$، $-2$، $0$، و $2$، برای یافتن اکسترمم های موضعی (local extrema) این تابع استفاده کرده اید: $(-2,64)$، $(2,-64)$. در این بخش اتفاقاتی که در نقاط دیگر این تابع رخ می دهند، مورد بررسی قرار می گیرد ـــ به طور مشخص، اینکه در کجا تقعر رو به پایین یا تقعر رو به بالا دارد و جاهاییکه تقعر تعویض می شود (نقاط عطف).

فرآیند یافتن تقعر (concavity) و نقاط عطف (inflection points) مشابه استفاده از آزمون مشتق اول و نمودار علامت، برای یافتن اکسترمم های موضعی می باشد، با این تفاوت که در اینجا از مشتق دوم استفاده می کنید. در اینجا کاری که برای یافتن بازۀ تقعر و نقاط عطف در $f(x)=3x^5-20x^3$ باید انجام دهید، می بینید:

مشتق دوم $f$ را بیابید. $$
f(x)=3x^5-20x^3 \\
f'=15x^4-60x^2 \\
f''=60x^3-120x
$$
مشتق دوم را برابر با صفر قرار دهید و آن را حل کنید. $$
60x^3-120x=0 \\
60x(x^2-2)=0 \\
\begin{array}{c c c}
60x=0 & \text{ or } & x^2-2=0 \\
x=0 & & x^2=2 \\
& & x=\pm\sqrt{2}
\end{array}
$$
تعیین کنید که آیا مشتق دوم به ازاء هیچ مقدار $x$ای تعریف نشده می باشد.
$f''=60x^3-120x$ به ازاء تمامی اعداد حقیقی (real numbers) تعریف شده می باشد، بنابراین مقدار $x$ دیگری وجود ندارد که به لیست بدست آمده از مرحلۀ 2 اضافه کنیم. بنابراین، لیست کامل برابر با $-\sqrt{2}$، $0$، و $\sqrt{2}$ می باشد.
مراحل 2 و 3 چیزی را به شما می دهند که می توانید آن را "اعداد بحرانی مشتق دوم" $f$ بنامید، زیرا آنها مشابه اعداد بحرانی بدست آمده از $f$ با استفاده از مشتق اول می باشند. اما تا آنجا که من اطلاع دارم، این مجموعه اعداد نام خاصی ندارند. چیز مهمی که باید بدانید اینست که این لیست از صفرهای $f''$ بعلاوۀ هر مقدار $x$ای که در آن $f''$ تعریف نشده باشد، تشکیل شده است.
این اعداد را بر روی یک خط اعداد قرار دهید و ناحیه ها را با مشتق دوم تست کنید.
از $-2$، $-1$، $1$، و $2$ به عنوان اعداد تستی استفاده کنید.
$$f''(x)=60x^3-120x \\
f''(-2)=-240 \\
f''(-1)=60 \\
f''(1)=-60 \\
f''(2)=240 $$
شکل 9-11 این نمودار علامت (sign graph) را نشان می دهد.

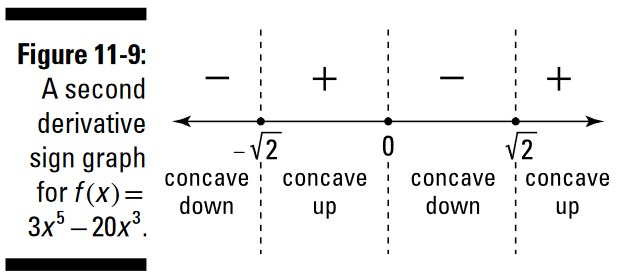
علامت مثبت در این نمودار علامت به شما می گوید که آن تابع در آن بازه، تقعر رو به بالا (concave up) دارد؛ علامت منفی بدین معناست که تقعر رو به پایین (concave down) دارد. این تابع (معمولاً) در هر مقدار $x$ای که این علامت از مثبت به منفی یا برعکس تغییر می کند، دارای یک نقطۀ عطف (inflection point) می باشد.

از آنجا که این علامتها در $-\sqrt{2}$، $0$، و $\sqrt{2}$، تغییر می کنند، و از آنجا که این سه عدد، صفرهایی از $f''$ هستند، نقاط عطف در این مقادیر $x$ رخ می دهند. با این حال، اگر مسأله ای داشته باشید که در آن علامتها در عددی تغییر کنند که $f''$ در آنجا تعریف نشده باشد، قبل از اینکه نتیجه گیری کنید در آنجا یک نقطۀ عطف وجود دارد، شما باید یک چیز دیگر را بیازمایید. یک نقطۀ عطف تنها زمانی در یک مقدار $x$ معین وجود دارد که شما بتوانید در آن عدد یک خط مماس (tangent line) روی آن تابع ترسیم کنید. اگر مشتق اول در آن عدد موجود باشد، یا اگر خط مماس عمودی باشد، این مورد رخ می دهد.
این سه مقدار $x$ را در $f$ جایگذاری کنید تا مقادیر تابع را برای این سه نقطۀ عطف بیابید. $$f(x)=3x^5-20x^3 \\
f(-\sqrt{2}) \approx -39.6 \\
f(0)= \\
f(\sqrt{2}) \approx -39.6 $$
جذر $2$ در حدود $1.4$ می باشد، بنابراین نقاط عطفی در حدود $(-1.4,39.6)$، $(0,0)$، و در حدود $(1.4,-39.6)$ می باشند. کار تمام است.