شما می توانید با بررسی نمودار توابع و مقایسۀ ویژگی های مهم آنها در کنار یکدیگر، چیزهای زیادی در مورد آن توابع و مشتق های آنها بیاموزید. بیایید با همان مثال تکراری این فصل، \(f(x)=3x^5-20x^3\)، کار را ادامه دهیم؛ ما قصد داریم تا در امتداد \(f\) از چپ به راست سفر کنیم (شکل 11-11 را ببینید)، بر روی نقاط جذاب آن مکث کنید، و همچنین توجه کنید که در نمودار \(f'=15x^4-60x^2\) در همان نقاط یکسان چه چیزی رخ می دهد. اما قبل از آن، هشدار طولانی زیر شکل را بخوانید.







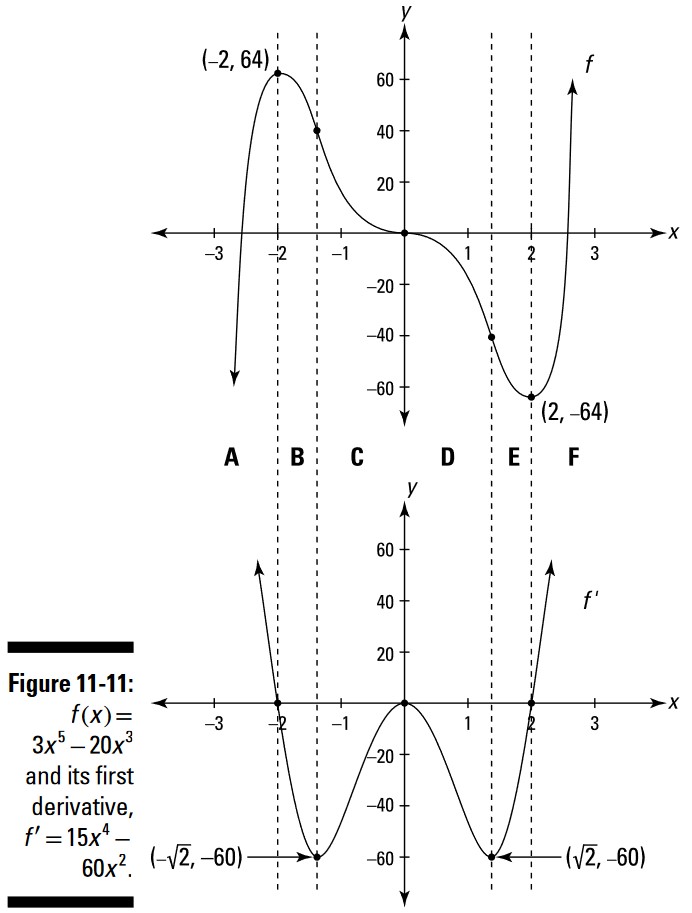
اوکی، بیایید به \(f\) و مشتق آن در شکل 11-11 بازگردیم. اگر از سمت چپ آغاز کنیم و به سمت راست سفر کنیم، \(f\) تا ماکزیمم نسبی در \((-2,64)\) افزایش می یابد. آن رو به بالا می رود، بنابراین شیب آن مثبت می باشد، اما تندی آن کمتر و کمتر می شود، بنابراین شیب آن کاهش می یابد ـــ این شیب کاهش می یابد تا در قله به صفر برسد. این با نمودار \(f'\) متناظر است (با شیب) که آنهم مثبت است (زیرا بالای محور \(x\) قرار دارد) اما همچنان که رو به سمت پایین و نقطۀ \((-2,0)\) می رود، کاهش می یابد. بیایید کل سفر شما در امتداد \(f\) و \(f'\) را با لیست قواعد زیر، خلاصه کنیم.

• یک بازۀ در حال افزایش بر روی یک تابع با بازه ای بر روی مشتق آن که مثبت باشد (یا در صورتی که آن تابع دارای یک نقطۀ عطف افقی است، صفر باشد)، متناظر است. به عبارت دیگر، یک بازۀ در حال افزایش در یک تابع با بخشی از نمودار مشتق که در بالای محور \(x\) قرار دارد، متناظر است (یا در مورد یک نقطۀ عطف افقی، آن محور را در یک نقطۀ واحد لمس کرده باشد). بازه های \(A\) و \(F\) در شکل 11-11 را ببینید.
  
  
• یک ماکزیمم نسبی بر روی نمودار یک تابع (مانند \((-2,64)\)) با یک صفر (یک طول از مبدأ) در یک بازه از نمودار مشتق آن که از محور \(x\) رو به پایین عبور می کند، متناظر است (مانند \((-2,0)\)).
  
  
  در نمودار یک مشتق، شما یک محور \(m\) بدست می آورید. هنگامی که به نقاط مختلف بر روی نمودار مشتق می نگرید، فراموش نکنید که، مختصات \(y\) از یک نقطه، مانند \((-2,0)\)، بر روی نمودار مشتق اول، شیب تابع اصلی، و نه ارتفاع آن، را به شما می گوید. به محور \(y\) در نمودار مشتق اول به عنوان محور شیب (slope-axis) یا محور \(m\) (m-axis) فکر کنید؛ شما می توانید به نقاط عمومی در نمودار مشتق اول به عنوان نقاط دارای مختصات \((x,m)\) فکر کنید.
  
  
  
• یک بازۀ در حال کاهش بر روی یک تابع با یک بازۀ منفی (یا اگر آن تابع یک نقطۀ عطف افقی داشته باشد، صفر) بر روی نمودار مشتق آن متناظر می باشد. بازۀ منفی بر روی نمودار مشتق زیر محور \(x\) قرار دارد (یا در مورد یک نقطۀ عطف افقی، نمودار مشتق محور \(x\) را در یک نقطۀ واحد لمس می کند). بازه های \(B\)، \(C\)، \(D\)، و \(E\) در شکل 11-11 را ببینید (اما آنها را به عنوان یک بخش واحد در نظر بگیرید)، که در آن \(f\) تمام مسیر از ماکزیمم نسبی در \((-2,64)\) تا مینیمم نسبی در \((64,-2)\) را رو به پایین می رود و در آن \(f'\) بین \((-2,0)\) و \((2,0)\) منفی می باشد به جز نقطۀ \((0,0)\) در \(f'\) که با نقطۀ عطف افقی در \(f\) متناظر می باشد.
  
  
• یک مینیمم نسبی بر روی نمودار یک تابع با یک صفر (یک طول از مبدأ) بر روی یک بازه از نمودار مشتق آن که از محور \(x\) عبور کرده و رو به بالا می رود، متناظر است (مانند \((2,0)\)).
  

حالا بیایید یک سفر دومی را در امتداد \(f\) برویم که در آن بازه های تقعر و نقاط عطف آن را در نظر گرفته باشیم. ابتدا بازه های \(A\) و \(B\) در شکل 11-11 را در نظر بگیرید. نمودار \(f\) تقعر رو به پایین دارد ـــ که به همان معنای شیب در حال کاهش می باشد ـــ تا اینکه به نقطۀ عطف قرار گرفته در حدود \((-1.4,39.6)\) برسد.

بنابراین، نمودار \(f'\) کاهش می یابد تا در حدود \((-1.4,-60)\) به انتهای خط برسد. این مختصات به شما می گوید که این نقطۀ عطف در \(-1.4\) بر روی \(f\) دارای شیب \(-60\) می باشد. توجه داشته باشید که این نقطۀ عطف بر روی \(f\) در \((-1.4,39.6)\) تندترین نقطه در آن بخش از تابع می باشد، اما دارای کمترین شیب می باشد، زیرا شیب آن منفی و بزرگتر از شیب هر نقطۀ همجوارش می باشد.

بین \((-1.4,39.6)\) و نقطۀ عطف بعدی در \((0,0)\)، تابع \(f\) تقعر رو به بالا دارد، که به همان معنای شیب در حال افزایش می باشد. بنابراین نمودار \(f'\) از حدود \(-1.4\) تا جایی که در \((0,0)\) به یک ماکزیمم نسبی برسد، افزایش می یابد. بازۀ \(C\) در شکل 11-11 را ببینید. بیایید یک استراحت کوتاه در سفرمان داشته باشید و چند قانون دیگر را ببینیم.

• یک بازۀ دارای تقعر رو به پایین بر روی نمودار یک تابع با یک بازۀ در حال کاهش بر روی نمودار مشتق آن متناظر است (بازه های \(A\)، \(B\)، و \(D\) در شکل 11-11). و یک بازۀ دارای تقعر رو به بالا بر روی آن تابع با یک بازۀ در حال افزایش بر روی مشتق آن متناظر است (بازه های \(C\)، \(E\)، و \(F\)).
  
  
• یک نقطۀ عطف بر روی یک تابع (به استثناء یک نقطۀ عطف عمودی که در آن مشتق تعریف نشده است) با یک اکسترمم موضعی بر روی نمودار مشتق آن متناظر می باشد. یک نقطۀ عطف با کمترین شیب (در شیب های همجوارش) با یک مینیمم موضعی بر روی نمودار مشتق، متناظر است؛ یک نقطۀ عطف با بیشترین شیب (در شیب های همجوارش) با یک ماکزیمم موضعی بر روی نمودار مشتق، متناظر است.
  

سفرمان را از سر می گیریم، بعد از \((0,0)\)، \(f\) تقعر رو به پایین دارد تا اینکه به نقطۀ عطف قرار گرفته در حدود \((1.4,39.6)\) برسد ـــ این با بخش در حال کاهش بر روی \(f'\) از \((0,0)\) تا مینیمم آن در \((1.4,-60)\) متناظر می باشد (بازۀ \(D\) در شکل 11-11). در نهایت \(f\) بقیۀ مسیر را تقعر رو به بالا دارد، که با بخش در حال افزایش \(f'\) که از \((1.4,-60)\) آغاز می گردد، متناظر است (بازه های \(E\) و \(F\) در شکل).

خوب، این تقریباً شما را به انتهای جاده می رساند. عقب و جلو رفتن بین نمودار یک تابع و نمودار مشتق آن در ابتدا می تواند خیلی سخت باشد. برای همین اگر سرگیجه گرفتید، استراحت کوتاهی بکنید و بعداً به این ماجراها بازگردید.

اگر تا اینجای کار نتوانسته ام شما را دیوانه کنم، شاید این نکتۀ آخر من را به نتیجۀ مطلوب برساند. دوباره نگاهی به نمودار مشتق، \(f'\) ، در شکل 11-11 و همچنین نمودار علامت برای \(f''\) در شکل 9-11 بیندازید. آن نمودار علامت، از آنجا که یک نمودار علامت مشتق دوم می باشد، دقیقاً (خوب، تقریباً دقیق) همان ارتباطاتی را با نمودار \(f'\) در بردارد که \(f'\) به عنوان یک نمودار علامت مشتق اول با نمودار یک تابع معمولی در بردارد. به عبارت دیگر، بازه های منفی در نمودار علامت در شکل 9-11 (در سمت چپ \(-\sqrt{2}\) و بین \(0\) و \(\sqrt{2}\)) به شما نشان می دهند که کجا نمودار \(f'\) کاهش می یابد؛ بازه های مثبت بر روی نمودار علامت (بین \(\sqrt{2}\) و \(0\) تا سمت راست \(\sqrt{2}\)) به شما نشان می دهد کجا \(f'\) افزایش می یابد. و نقاطی که در آنها علامتها از مثبت به منفی، یا برعکس، تغییر می کنند (در \(-\sqrt{2}\)، \(0\) ، و \(\sqrt{2}\)) به شما نشان می دهد کجا \(f'\) دارای یک اکسترمم موضعی است. درکش بسیار سخت است، اینطور نیست؟