نرخ های مرتبط (related rates)

فرض کنید مشغول پر کردن استخر شنایتان هستید و می دانید آب با چه سرعتی از شلنگ شما بیرون می آید، و می خواهید محاسبه کنید که سطح آب در استخر با چه سرعتی بالا می آید. شما یک نرخ را می دانید (آب با چه سرعتی به درون استخر ریخته می شود)، و می خواهید نرخ دیگری را تعیین نمایید (با چه سرعتی سطح آب بالا می آید). این نرخ ها، نرخ های مرتبط (related rates) نامیده می شوند، زیرا یکی به دیگری بستگی دارد ـــ هر چقدر آب سریعتر به درون ریخته شود، سطح آب سریعتر بالا می آید. در یک مسالۀ نرخ مرتبط معمولی (مانند همین مسأله ای که شرح داده شد)، نرخ یا نرخ ها در اطلاعات داده شده ثابتند، تغییر نمی کنند، و شما باید یک نرخ مرتبط را بیابید که با زمان تغییر می کند. شما باید این نرخ مرتبط را در یک نقطۀ خاص از زمان مشخص کنید. اگر این کاملاً واضح و بدون ابهام نیست، هنگامی که به مسأله های بعدی بپردازید، ظرف یک دقیقه منظور مرا خواهید دانست.

حل کردن این مسأله ها در ابتدا می تواند ترفندآمیز باشد، اما با تمرین روش حل آنها را خواهید آموخت. استراتژی ها و نکات یک کمک بزرگ هستند ـــ بیایید سه مثال را انجام بدهیم.

باد کردن یک بادکنک

شما بادکنکی را با نرخ $300$ اینچ مکعب در دقیقه باد می کنید. هنگامی که شعاع این بادکنک به $3$ اینچ می رسد، این شعاع با چه سرعتی افزایش می یابد؟

شکلی ترسیم کنید، آن را با هر اندازۀ بدون تغییر برچسب گذاری کنید (در این مسالۀ سادۀ غیرمعمول هیچ اندازۀ بدون تغییری وجود ندارد) و اطمینان حاصل کنید که به هر چیزی در این مسأله که تغییر می کند، یک متغیر را تخصیص داده باشید (مگر اینکه به مسأله نامرتبط باشد). شکل 6-12 را ببینید.

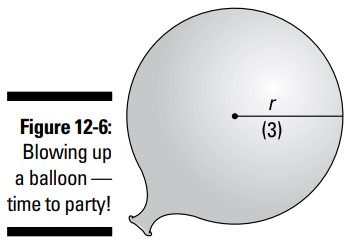
توجه کنید که شعاع موجود در شکل 6-12 با متغیر $r$ نامگذاری شده است. این شعاع نیاز به یک متغیر دارد زیرا به محض اینکه این بادکنک باد می شود، این شعاع تغییر می کند. من $3$ را در داخل یک جفت پرانتز قرار داده ام تا روی این نکته تاکید کنم که عدد $3$ یک اندازۀ بدون تغییر نمی باشد. مسأله از شما می خواهد، هنگامیکه این شعاع برابر با $3$ اینچ است، چیزی را تعیین کنید، اما یادتان باشد که این شعاع به طور مداوم تغییر می کند.

در حال تغییر یا بدون تغییر؟ در مسأله های نرخ های مرتبط، مهم است که بین آن چیزی که تغییر می کند و آن چیزی که تغییر نمی کند، تمایز قائل شوید.

حجم این بادکنک نیز تغییر می کند، بنابراین برای حجم آن نیز نیاز به یک متغیر، $V$، دارید. شما می توانید یک $V$ بر روی شکلتان قرار دهید تا حجم در حال تغییر را نشان دهد، اما روش ساده ای برای نشان گذاری بخشی از این بادکنک با یک $V$ مشابه آنچه با یک $r$ نشان دادید، نمی باشد.
نرخ داده شده و نرخی که از شما خواسته شده است تا تعیینش کنید را به شکل مشتق هایی با توجه به زمان فهرست کنید.
شما این بادکنک را $300$ اینچ مکعب در دقیقه باد می کنید. این یک نرخ است ـــ یک تغییر در حجم (اینچ های مکعب) در هر تغییر در زمان (دقیقه ها). بنابراین:
$$\frac{dV}{dt}=300 \text{ cubic inches per minute}$$

cubic inches per minute: اینچ مکعب در دقیقه

شما باید یک نرخ مرتبط را بدست آورید، مشخصاً اینکه شعاع با چه سرعتی تغییر می کند، بنابراین:
$$\frac{dr}{dt} = ?$$
فرمولی بنویسید که متغیرهای موجود در این مسأله مانند $V$ و $r$ را به یکدیگر مرتبط کند.
در اینجا فرمول حجم کره را می بینید:
$$V=\frac{4}{3}\pi r^3$$
فرمولتان را با توجه به زمان، $t$، مشتق گیری کنید.
هنگامی که در یک مسالۀ نرخ های مرتبط، مشتق گیری می کنید، با تمامی متغیرها مشابه آنچه که با $y$ها در یک مسالۀ مشتق گیری ضمنی معمولی برخورد می شود، رفتار می گردد.
$$\frac{dV}{dt}=\frac{4}{3} \pi \cdot 3 r^2 \frac{dr}{dt} \\
=4\pi r^2 \frac{dr}{dt}$$
شما نیاز دارید تا $\frac{dr}{dt}$ را درست مانند روشی که یک $y'$ یا $\frac{dy}{dx}$ را در یک مشتق گیری ضمنی می افزایید، اضافه کنید.
مقادیر معلوم برای نرخ و متغیرها از مرحلۀ 4 را در این معادله جایگذاری کنید، و سپس آن را برای بدست آوردن چیزی که از شما خواسته شده تعیین نمایید، حل کنید.
به شما داده شده است که $\frac{dV}{dt}=300$، و از شما خواسته شده است که $\frac{dr}{dt}$ را هنگامیکه $r=3$ است، تعیین کنید، بنابراین این اعداد را جایگذاری کنید و آن را برای بدست آوردن $\frac{dr}{dt}$ حل کنید.

قبل از جایگذاری مشتق گیری کنید. اطمینان حاصل کنید که قبل از اینکه اطلاعات داده شده را در مجهول ها جایگذاری کنید (مرحلۀ 5)، ابتدا مشتق گیری کرده باشید (مرحلۀ 4).

$$\frac{dV}{dt}=4 \pi r^2 \frac{dr}{dt} \\
300 = 4\pi \cdot 3^2 \frac{dr}{dt}\\
300 = 36 \pi \frac{dr}{dt} \\
\frac{300}{36 \pi} =\frac{dr}{dt} \\
\frac{dr}{dt} \approx 2.65 \text{ inches per minute}$$

بنابراین هنگامیکه این شعاع برابر با $3$ اینچ باشد، با نرخ حدود $2.65$ اینچ بر دقیقه، در حال افزایش می باشد. به تمام بادکنک هایی که از بچگی تا الان باد کرده اید فکر کنید. اکنون در نهایت پاسخ سوالی را که تمام این سالها شما را آزار می داد، می دانید!

راستی، اگر به جای $3$، عدد $5$ را در $r$ جایگذاری کنید، به پاسخی در حدود $0.95$ اینچ بر دقیقه می رسید. این با تجربۀ بادکنک باد کردن شما مطابقت دارد: هرچقدر بادکنک بزرگتر شود، رشد آن آهسته تر می گردد. فکر خوبی است که هر از گاهی چیزهایی مانند این را بررسی کنید تا ببینید که ریاضیات با درک عام شما مطابقت دارد.

پر کردن یک آبشخور

در اینجا مسالۀ نرخ های مرتبط دیگری داریم. یک آبشخور با غذای مخصوص خوکها پر شده است. طول این آبشخور $10$ فوت می باشد، و سطح مقطع (cross-section) آن یک مثلث متساوی الساقین با قاعدۀ $2$ فوت و ارتفاع $2$ فوت و $6$ اینچ می باشد (البته رأس آن در انتهایش می باشد). غذای خوکها با نرخ $5$ فوت مکعب در دقیقه به داخل آبشخور ریخته می شود. هنگامیکه عمق این غذاها برابر با $1$ فوت و $3$ اینچ می باشد، سطح غذاها با چه سرعتی افزایش می یابد؟

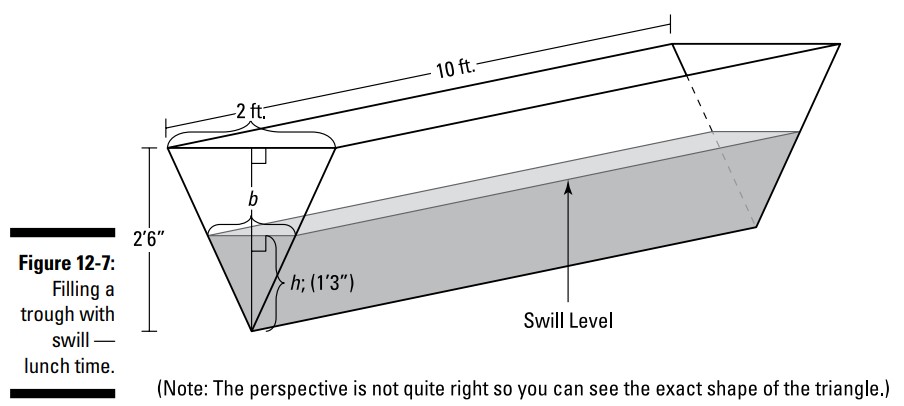
یک شکل بکشید، و آن را با هر اندازه گیری بدون تغییر برچسب گذاری کنید و به هر چیزی که تغییر می کند، متغیری را تخصیص بدهید. شکل 7-12 را ببینید.
توجه داشته باشید که شکل 7-12 ابعاد بدون تغییر این آبشخور را، $2$ فوت، $2$ فوت و $6$ اینچ، و $10$ فوت ، نشان می دهد، و اینکه این ابعاد اسامی متغیر مانند $l$ برای طول (length) یا $h$ برای ارتفاع (height) را ندارند. و به چیزهای در حال تغییر توجه کنید ـــ ارتفاع (یا عمق) غذاها و عرض سطح مقطع غذاها (که با عمیق تر شدن غذاها، وسیع تر می گردد) ـــ دارای اسامی متغیر، $h$ برای ارتفاع و $b$ برای قاعده (base) می باشند (دلیل اینکه به جای عرض از قاعده استفاده کردم اینست که در واقع این عرض همان قاعدۀ یک شکل مثلث وارونه است که توسط غذاها ایجاد شده است). حجم این غذاها نیز در حال تغییر است، بنابراین می توانید آن را $V$ بنامید.
نرخ داده شده و نرخی که از شما خواسته شده تا پیدا کنید را به شکل مشتق هایی با توجه به زمان، لیست کنید. $$\frac{dV}{dt}=5 \text{ cubic feet per minute} \\
\frac{dh}{dt}=?$$
1. فرمولی بنویسید که متغیرهای موجود در این مسأله را به یکدیگر مرتبط کند: $V$، $h$، و $b$.
  من کاملاً مطمئنم که شما فرمول حجم یک منشور قائم (right prism) را به خاطر می آورید (شکل غذاها در آبشخور):
  $$V=\text{(area of base)(height)}$$
  
  area of base: مساحت قاعده
  height: ارتفاع
  
  توجه داشته باشید که این قاعده، قاعدۀ منشور می باشد (کل مثلث قرار گرفته در انتهای آبشخور)، و نه قاعدۀ مثلث که در شکل 7-12 با $b$ برچسب گذاری شده است. همچنین، این ارتفاع، ارتفاعِ منشور می باشد (طول آبشخور)، و نه ارتفاعی که در شکل 7-12 با $h$ برچسب گذاری شده است. در مورد این آشفتگی ها متاسفم. با آن کنار بیایید.
  
  مساحت قاعدۀ مثلثی شکل برابر با $\frac{1}{2}bh$، و ارتفاع این منشور برابر با $10$ فوت می باشد، بنابراین این فرمول به این تبدیل می شود:
  $$V=\frac{1}{2}bh \cdot 10 \\
  V=5 bh$$
  اکنون، برخلاف فرمول مثال بادکنک، این فرمول شامل یک متغیر، $b$ می باشد، که در لیست مشتق هایتان در مرحلۀ 2 نمی بینید. بنابراین مرحلۀ 3 یک بخش دومی دارد ـــ خلاص شدن از شر این متغیر اضافی.
2. معادله ای را بیابید که این متغیر ناخواسته، $b$ ، را به برخی متغیرهای دیگر در مسأله مرتبط سازد، تا بتوانید یک جایگذاری ایجاد کنید که شما را فقط با متغیرهای $V$ و $h$ تنها بگذارد.
  وجه مثلثی شکل غذاهای داخل آبشخور مشابه با وجه مثلثی شکل خود آبشخور می باشد، بنابراین قاعده و ارتفاع این مثلث ها متناسب (proportional) می باشند. (از هندسه به خاطر بیاورید که مثلث های متشابه، مثلث هایی هم شکل می باشد؛ اضلاع آنها متناسب می باشند.) بدین ترتیب:
  $$\frac{b}{2} = \frac{h}{2.5} \\
  2.5 b = 2h \\
  b = \frac{2h}{2.5} \\
  b = 0.8 h$$
  
  یادداشت مترجم: در این مسأله اگر دقت کنید مقدار $\text{2'6"}$ به $2.5$ فوت تغییر یافته است. مراقب باشید که دچار این اشتباه نگردید که $\text{2'6"}$ (2 فوت و 6 اینچ) را با $2.6$ فوت اشتباه بگیرید. هر یک فوت برابر با $12$ اینچ می باشد و بنابراین $2$ فوت و $6$ اینچ برابر با $(2 \times 12)+6=24+6=30$ اینچ می باشد. بنابراین $2$ فوت و $6$ اینچ برابر با $2.5$ فوت می باشد، زیرا $(2.5 \times 12)=30$ .
  
  مراقب مثلث های متشابه باشید. در مسأله های نرخ های مرتبط، مثلث های متشابه (Similar triangles) بسیار ظاهر می شوند. هرگاه که مسأله ای شامل یک مثلث، یک منشور مثلثی شکل، یا یک شکل مخروط باشد، حواستان به آنها باشد.
  
  اکنون، $0.8h$ را از مرحلۀ $3.a$ در $b$ جایگذاری کنید.
  $$V=5bh \\
  V=5 \cdot 0.8h \cdot h \\
  V=4h^2$$
این معادله را با توجه به $t$ مشتق گیری کنید. $$\frac{dV}{dt}=8h\frac{dh}{dt}$$
(قانون توان همراه با مشتق گیریِ ضمنیِ $\frac{dh}{dt}$)
مقادیر معلوم برای نرخ و متغیرها از معادله مرحلۀ 4 را جایگذاری کنید و سپس حل کنید.
شما می دانید که $\frac{dV}{dt} = 5 \text{ cubic feet per minute}$، و می خواهید $\frac{dh}{dt}$ را هنگامی که $h$ برابر با $1$ فوت و $3$ اینچ، یا $1.25$ فوت می باشد، تعیین کنید، بنابراین $5$ و $1.25$ را جایگذاری کرده و آن را برای بدست آوردن $\frac{dh}{dt}$ حل کنید:
$$\frac{dV}{dt}=8h\frac{dh}{dt} \\
5=8 \cdot 1.25 \cdot \frac{dh}{dt} \\
5 = 10 \cdot \frac{dh}{dt} \\
\frac{dh}{dt} = \frac{1}{2}$$

تمام شد. هنگامی که عمق غذا برابر با $1$ فوت و $3$ اینچ باشد، سطح غذای خوکها با نرخ $\frac{1}{2}$ فوت بر دقیقه بالا می آید.

تقاطع جاده ها

برای مسالۀ نرخ های مرتبط رایج دیگری آماده هستید؟ یک خودرو تقاطعی را با سرعت $50$ مایل بر ساعت به سمت شمال، ترک می کند، خودروی دیگری رو به سمت غرب و با سرعت $40$ مایل بر ساعت بسوی این تقاطع رانندگی می کند. در یک نقطه، خودروی عازم شمال سه دهم مایل در سمت شمال این تقاطع قرار دارد، و خودروی عازم غرب، در چهار دهم یک مایلی شرق آن می باشد. در این نقطه، مسافت بین این دو خودرو، با چه سرعتی تغییر می کند؟

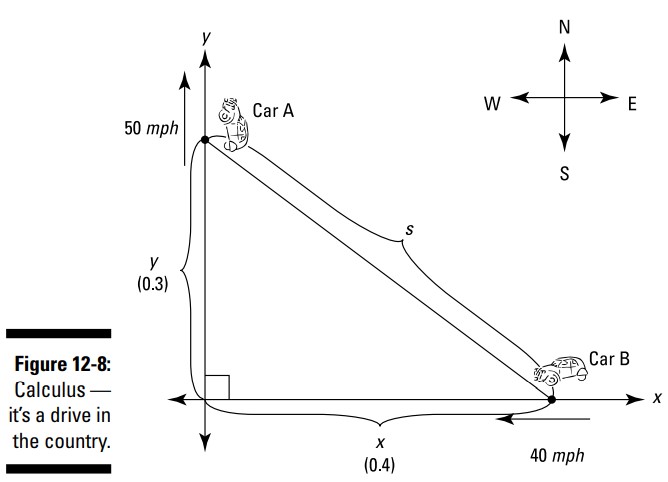
کارهای ترسیم شکل را انجام دهید. شکل 8-12 را ببینید.

متغیر یا ثابت؟ قبل از آنکه با این مسأله پیش بروید، می خواهم به یک مسالۀ مشابه اشاره کنم که در صورتیکه از یک کتاب درسی استاندارد حسابان استفاده می کنید، ممکن است با آن مواجه شوید. این مسأله شامل یک نردبان است که به یک دیوار تکیه داده است و از آن رو به سمت پایین سر می خورد. آیا می توانید ببینید که شکل مسأله نردبان بسیار شبیه شکل 8-12 است، با این تفاوت که در آنجا محور $y$ نشان دهندۀ دیوار است، و محور $x$ نشان دهندۀ زمین است، و آن خط مورب نیز نشان دهندۀ نردبان مورد اشاره است؟ این مسأله ها کاملاً مشابه هستند، اما یک تفاوت مهم بین آنها وجود دارد. فاصلۀ بین این دو خودرو در حال تغییر است، بنابراین خط مورب در شکل 8-12 با یک متغیر، $s$، نامگذاری شده است. از سوی دیگر، یک نردبان دارای طول ثابتی می باشد، بنابراین خط مورب موجود در مسالۀ نردبان شما احتمالاً با یک عدد برچسب گذاری شده باشد و نه با یک متغیر.
تمامی نرخ های داده شده و نرخ های مجهول را لیست کنید.
همینطور که خودروی $A$ به سمت شمال سفر می کند، مسافت $y$ با نرخ $50$ مایل بر ساعت رشد می کند. این یک نرخ است، یک تغییر در مسافت، به ازاء هر تغییر در زمان. بنابراین:
$$\frac{\text{change in distance in y direction
}}{\text{change in time}} = \frac{dy}{dt}=50 \text{ mph}$$
همچنانکه خودروی $B$ به سمت غرب سفر می کند، مسافت $x$ با نرخ $40$ مایل بر ساعت، کوچک می شود. این یک نرخ منفی است:
$$\frac{\text{change in distance in x direction}}{\text{change in time}}=\frac{dx}{dt}=-40 \text{ mph}$$
شما باید کشف کنید، $s$ با چه سرعتی تغییر می کند، بنابراین:
$$\frac{\text{change in distance in s direction}}{\text{change in time}}=\frac{ds}{dt}=?$$

change in distance in y direction: تغییر مسافت در جهت $y$
change in distance in x direction: تغییر مسافت در جهت $x$
change in distance in s direction: تغییر مسافت در جهت $s$
change in time: تغییر در زمان
فرمولی بنویسید که متغیرهای موجود در این مسأله را به یکدیگر مرتبط کند: $x$، $y$، و $s$.
قضیۀ فیثاغورث، $a^2+b^2=c^2$، شما را به مقصودتان در این مسالۀ مثلث قائم الزاویه می رساند. در این مسأله، $x$ و $y$ ساق های این مثلث قائم الزاویه هستند، و $s$ وتر آن است، بنابراین:
$$x^2+y^2=s^2$$

در مسأله های نرخ های مرتبط، قضیۀ فیثاغورث به وفور مورد استفاده قرار می گیرد. اگر در مسالۀ شما یک مثلث قائم الزاویه وجود داشته باشد، کاملاً محتمل است که $a^2+b^2=c^2$ فرمولی باشد که بدان نیاز دارید.

از آنجا که این فرمول شامل متغیرهای $x$، $y$، و $s$ می باشد که همگی در لیست مشتق های شما در مرحلۀ 2 ظاهر شده اند، نیازی نیست تا مانند کاری که در مسالۀ آبشخور انجام دادید، فرمول های را بپیچانید.
با توجه به $t$ مشتق گیری را انجام دهید. $$s^2 = x^2 + y^2 \\
2s \frac{ds}{dt} = 2x \frac{dx}{dt} + 2y \frac{dy}{dt}$$
(مشتق گیری ضمنی، همراه با قانون توان)
(به خاطر داشته باشید که در یک مسالۀ نرخ های مرتبط، با تمامی متغیرها مشابه $y$ها در مسأله های مشتق گیری ضمنی (implicit differentiation problem) برخورد می شود.)
جایگذاری کنید و آن را برای بدست آوردن $\frac{ds}{dt}$ حل کنید. $$x=0.4,y=0.3,\frac{dx}{dt}=-40,\frac{dy}{dt}=50, \text{ and } s= .....$$
چگونه می توانیم این معادله را برای بدست آوردن $\frac{ds}{dt}$ حل کنیم، مگر اینکه مقادیر سایر مجهول های موجود در این معادله را داشته باشیم؟ فقط کافیست دوباره از قضیۀ فیثاغورث استفاده کنیم.
$$s^2=x^2+y^2 \\
s^2 = 0.4^2 + 0.3^2 \\
s^2=0.16+0.09 \\
s^2=0.25 \\
s=\pm 0.5$$
شما می توانید پاسخ منفی را نادیده بگیرید، زیرا $s$ به صورت واضح دارای یک طول مثبت می باشد. بنابراین:
$$s=0.5$$
اکنون همه چیز را در معادلۀ تان جایگذاری کنید:
$$2s \frac{ds}{dt} = 2x \frac{dx}{dt} + 2y \frac{dy}{dt} \\
2 \cdot 0.5 \cdot \frac{ds}{dt} = 2 \cdot 0.4 \cdot (-40) + 2 \cdot 0.3 \cdot 50 \\
1 \cdot \frac{ds}{dt} = -32 + 30 \\
\frac{ds}{dt} = -2$$
این پاسخ منفی بدین معناست که مسافت، $s$، در حال کاهش می باشد.

بدین ترتیب، هنگامی که خودروی $A$ برابر با $3$ بلوک در شمال این تقاطع باشد، و خودروی $B$ برابر با $4$ بلوک در شرق آن باشد، مسافت بین آنها با نرخ $2$ مایل بر ساعت (mph) کاهش می یابد.