خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
مسأله های تجاری و اقتصادی

باور کنید یا نه، حسابان در دنیای واقعی تجارت و اقتصاد مورد استفاده قرار می گیرد ـــ حسابان را بیاموزید و سودتان را افزایش دهید! به من بگو: هنگامی که در بخشی از بالاشهر رانندگی می کنی و از کنار یک خانۀ بزرگ می گذری، اولین چیزی که به ذهنت می آید چیست؟ من شرط می بندم اینست: "اون خونه رو ببین! اون مرد (یا زن) حتماً حسابان بلد است!"

دوباره به شکل 3-13 و 4-13 در بخش قبلی در همین فصل، نگاه کنید. به خاطر بیاورید که مشتق و از این رو شیب \(y=\sqrt{x}\) در \((9,3)\) برابر با \(\frac{1}{6}\) است و اینکه خط تانژانت در این نقطه می تواند برای تقریب تابع نزدیک نقطۀ تماس، مورد استفاده قرار گیرد. بنابراین، همینطور که در امتداد این تابع از \(1\) تا \(9\) می روید، در حدود \(\frac{1}{6}\) بالا می روید. و بنابراین، \(\sqrt{10}\) در حدود \(\frac{1}{6}\) بیشتر از \(\sqrt{9}\) است. ریاضیات نهائی ها (marginals) دقیقاً به شیوۀ مشابهی کار می کند.
فرض کنید یک تابع هزینه دارید که مجموع هزینه، \(C(x)\) برای تولید \(x\) محصول را به شما می دهد. شکل 5-13 را ببینید.
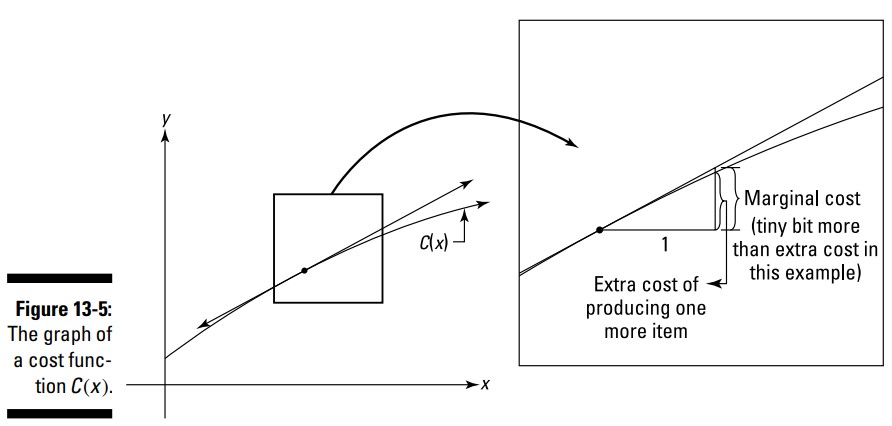
به مربع بزرگ شده در سمت راست شکل بنگرید. مشتق \(C(x)\) در نقطۀ تماس (point of tangency)، شیب این خط مماس (tangent line) را به شما می دهد، در .واقع به ازاء هر \(1\) واحد حرکت در امتداد این خط مماس به سمت راست، مقداری که بالا می روید را به شما می دهد. این مقدار در شکل با هزینۀ نهایی (marginal cost) برچسب گذاری شده است. حرکت به سمت راست به مقدار \(1\) واحد در امتداد این تابع هزینه (cost function)، افزایش در هزینۀ تولید (cost of producing) یک آیتم بیشتر را نشان می دهد. این با هزینۀ اضافی (extra cost) برچسب گذاری شده است. از آنجا که این خط مماس یک تقریب خوب از این تابع هزینه است، مشتق \(C\) ـــ که هزینۀ نهائی نامیده می شود ـــ برابر با افزایش تقریبی هزینۀ تولید یک محصول بیشتر می باشد. درآمد نهایی (Marginal revenue) و سود نهایی (marginal profit) به شیوۀ یکسانی کار می کنند.
قبل از اینکه مثالی شامل نهائی ها را انجام بدهید، یک کار دیگر هست که باید انجام شود. یک تابع تقاضا (demand function) به شما می گوید چندین محصول با قیمت داده شده، باید خریداری شود. مسلماً هرچقدر قیمت کمتر باشد، تقاضا بیشتر خواهد بود؛ و هر چقدر قیمت بیشتر باشد، تقاضا کمتر خواهد بود. شما فکر می کنید که تعداد خریداری شده باید تابعی از قیمت باشد ـــ قیمت را به آن وارد کنید و کشف کنید که افراد چندین محصول با آن قیمت می توانند خریداری کنند ـــ اما به طور سنتی یک تابع تقاضا برخلاف این نوشته می شود. قیمت به صورت تابعی از تعداد مورد نیاز بیان می شود. من می دانم که این اندکی عجیب به نظر می آید، اما نگران نباشید ـــ این تابع در هر دو جهت کار می کند. به آن اینگونه فکر کنید: اگر یک خرده فروش بخواهد تعداد خاصی از یک محصول را بفروشد، تابع تقاضا به آن خرده فروش می گوید که قیمت فروش را چگونه باید تنظیم کند.
اوکی، در اینجا مثالی داریم. یک تولید کننده تابع تقاضا را برای چیزهایی که تولید می کند، اینگونه مشخص ساخته است:
$$p=\frac{1000}{\sqrt{x}}$$
در این تابع \(p\) قیمت محصول تولیدی و \(x\) تعداد چیزهای مورد نیاز است. بهای تولید \(x\) محصول با تابع هزینۀ زیر تعیین می شود:
$$C(x)=10x+100 \sqrt{x} + 10,000$$
هزینۀ نهایی، درآمد نهایی، و سود نهایی را در \(x=100\) تعیین کنید. همچنین، اینکه چند محصول باید تولید شود، و اینکه برای تولید بیشترین سود، به چه قیمتی باید فروخته شوند، و اینکه ماکزیمم سود چیست؟
هزینۀ نهایی مشتق تابع هزینه می باشد، بنابراین مشتق آن را بگیرید و آن را در \(x=100\) ارزیابی کنید:
$$C(x)=10x+100\sqrt{x}+10,000 \\
C'(x)=10+\frac{50}{\sqrt{x}} \\
C'(100)=10+\frac{50}{\sqrt{100}} \\
=10+\frac{50}{10} \\
=15
$$
بنابراین، هزینۀ نهایی در \(x=100\) برابر با \($15\) می باشد ـــ این هزینۀ تقریبی برای تولید محصول \(101\)ام می باشد.
درآمد، \(R(x)\)، برابر با تعداد آیتم های فروخته شده، \(x\)، ضربدر قیمت، \(p\)، می باشد:
$$R(x)=x \cdot p \\
= x \cdot \frac{1000}{\sqrt{x}} \\
= \frac{1000x}{\sqrt{x}} \cdot \frac{\sqrt{x}}{\sqrt{x}} \\
=\frac{1000x \sqrt{x}}{x} \\
=1000\sqrt{x}$$
درآمد نهایی برابر با مشتق تابع درآمد می باشد، بنابراین مشتق \(R(x)\) را بگیرید و آن را در \(x=100\) ارزیابی کنید:
$$R(x)=1000 \sqrt{x} \\
R'(x) = \frac{500}{\sqrt{x}} \\
R'(100) = \frac{500}{\sqrt{100}} \\
= 50$$
بنابراین، درآمد تقریبی از فروش \(101\)امین محصول برابر با \($50\) می باشد.
سود، \(P(x)\)، برابر با درآمد منهای هزینه می باشد. بنابراین:
$$P(x)=R(x)-C(x) \\
=1000 \sqrt{x} - (10x + 100\sqrt{x} + 10,000) \\
= -10 x+900\sqrt{x}-10,000$$
سود نهایی برابر با مشتق تابع سود می باشد، بنابراین مشتق \(P(x)\) را بگیرید، و آن را در \(x=100\) ارزیابی کنید:
$$P(x)=-10x+900\sqrt{x}-10,000 \\
P'(x)=-10+\frac{450}{\sqrt{x}} \\
P'(100)=-10+\frac{450}{\sqrt{100}} \\
=-10+45 \\
=35$$
فروش \(101\)امین محصول، سود تقریبی \($35\) دلار را به همراه دارد.
این یک چیز بدیهی است. اگر تولید \(101\)امین محصول برای شما در حدود \($15\) هزینه بردارد، و شما آن را در حدود \($50\) بفروشید، سپس سود شما در حدود \($35\) خواهد بود.
من این کار را با روش طولانی تر انجام دادم زیرا برای مسالۀ زیر، شما به هر دو تابعِ سود، \(P(x)\)، و سود نهایی، \(P'(x)\)، نیاز خواهید داشت.
برای تعیین ماکزیمم سود، مشتق سود را ـــ که سود نهایی می باشد ـــ برابر با صفر قرار دهید، آن را برای بدست آوردن \(x\) حل کنید، و سپس نتیجه را در تابع سود، جایگذاری کنید:
$$P'(x)=-10+\frac{450}{\sqrt{x}} \\
0=-10+\frac{450}{\sqrt{x}} \\
10=\frac{450}{\sqrt{x}} \\
10\sqrt{x}=450 \\
\sqrt{x}=45 \\
x=2025$$
بنابراین، ماکزیمم سود زمانی رخ می دهد که \(2,025\) محصول فروخته شود. آن را در \(P(x)\) جایگذاری کنید:
$$P(x)=-10x+900\sqrt{x}-10,000 \\
P(2025)=-10 \cdot 2025 + 900 \sqrt{2025} - 10,000 \\
=-20,250 + 900 \cdot 45 - 10,000 \\
=10,250$$
بدین ترتیب، ماکزیمم سود برابر با \($10,250\) می باشد.
در پایان، تعداد فروخته شده را در تابع تقاضا جایگذاری کنید، تا بهای ماکزیمم سود را بدست آورید:
$$p=\frac{1000}{\sqrt{x}} \\
p=\frac{1000}{\sqrt{2025}} \\
\approx 22.22$$
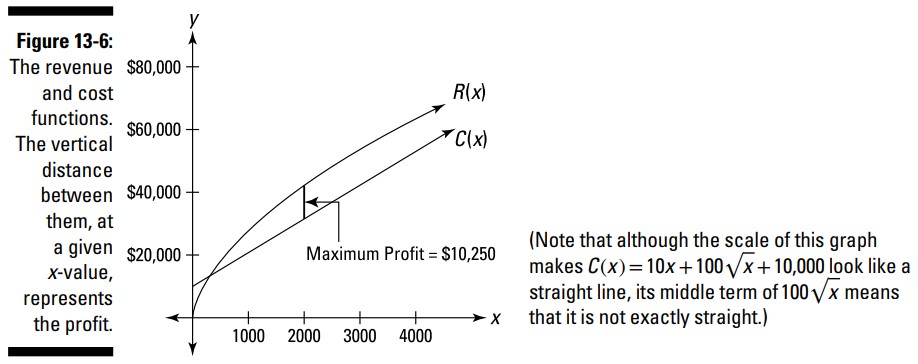
بنابراین ماکزیمم سود \($10,250\) زمانی رخ می دهد که قیمت برابر با \($22.22\) باشد. در این قیمت، \(2,025\) محصول فروخته خواهد شد. شکل 6-13 این نتایج را خلاصه کرده است. توجه داشته باشید از آنجاییکه سود برابر با درآمد منهای هزینه می باشد، مسافت عمودی یا شکاف بین درآمد و هزینه در یک مقدار \(x\) مشخص، سود در آن مقدار \(x\) را نتیجه می دهد. ماکزیمم سود زمانی رخ می دهد که این شکاف در بالاترین حد ممکنش باشد.
و در اینجا چیز دیگری داریم. از آنجا که ماکزیمم سود در جایی رخ می دهد که \(P'(x)=0\)، و از آنجا که \(P'(x)=R'(x)-C'(x)\)، نتیجه این می شود که این سود در \(0=R'(x)-C'(x)\) در بالاترین حد ممکنش می باشد ـــ به عبارت دیگر، \(R'(x)=C'(x)\). و هنگامی که \(R'(x)=C'(x)\)، شیب خط های مماس این توابع برابر می باشند. بنابراین، اگر قرار باشد تا خط های مماسی را برای \(R(x)\) و \(C(x)\) ترسیم کنید که شکاف بین آنها در بالاترین حد باشد، این خط های مماس با یکدیگر موازی خواهند بود.

مدیریت نهائی ها (marginals) در اقتصاد
دوباره به شکل 3-13 و 4-13 در بخش قبلی در همین فصل، نگاه کنید. به خاطر بیاورید که مشتق و از این رو شیب \(y=\sqrt{x}\) در \((9,3)\) برابر با \(\frac{1}{6}\) است و اینکه خط تانژانت در این نقطه می تواند برای تقریب تابع نزدیک نقطۀ تماس، مورد استفاده قرار گیرد. بنابراین، همینطور که در امتداد این تابع از \(1\) تا \(9\) می روید، در حدود \(\frac{1}{6}\) بالا می روید. و بنابراین، \(\sqrt{10}\) در حدود \(\frac{1}{6}\) بیشتر از \(\sqrt{9}\) است. ریاضیات نهائی ها (marginals) دقیقاً به شیوۀ مشابهی کار می کند.
هزینۀ نهائی (Marginal cost)، درآمد نهائی (marginal revenue)، و سود نهائی (marginal profit) بسیار شبیه تقریب خطی (linear approximation) کار می کند. هزینۀ نهائی، درآمد نهائی، و سود نهائی، همگی شامل اینست که همینطور که \(1\) واحد به سمت راست می روید، یک تابع چقدر بالا (یا پایین) می رود ـــ درست مانند تقریب خطی.
فرض کنید یک تابع هزینه دارید که مجموع هزینه، \(C(x)\) برای تولید \(x\) محصول را به شما می دهد. شکل 5-13 را ببینید.

به مربع بزرگ شده در سمت راست شکل بنگرید. مشتق \(C(x)\) در نقطۀ تماس (point of tangency)، شیب این خط مماس (tangent line) را به شما می دهد، در .واقع به ازاء هر \(1\) واحد حرکت در امتداد این خط مماس به سمت راست، مقداری که بالا می روید را به شما می دهد. این مقدار در شکل با هزینۀ نهایی (marginal cost) برچسب گذاری شده است. حرکت به سمت راست به مقدار \(1\) واحد در امتداد این تابع هزینه (cost function)، افزایش در هزینۀ تولید (cost of producing) یک آیتم بیشتر را نشان می دهد. این با هزینۀ اضافی (extra cost) برچسب گذاری شده است. از آنجا که این خط مماس یک تقریب خوب از این تابع هزینه است، مشتق \(C\) ـــ که هزینۀ نهائی نامیده می شود ـــ برابر با افزایش تقریبی هزینۀ تولید یک محصول بیشتر می باشد. درآمد نهایی (Marginal revenue) و سود نهایی (marginal profit) به شیوۀ یکسانی کار می کنند.
تعریف هزینۀ نهائی، درآمد نهائی، و سود نهائی:
-
هزینۀ نهایی برابر با مشتق تابع هزینه می باشد.
-
درآمد نهائی برابر با مشتق تابع درآمد می باشد.
-
سود نهائی برابر با مشتق تابع سود می باشد.
قبل از اینکه مثالی شامل نهائی ها را انجام بدهید، یک کار دیگر هست که باید انجام شود. یک تابع تقاضا (demand function) به شما می گوید چندین محصول با قیمت داده شده، باید خریداری شود. مسلماً هرچقدر قیمت کمتر باشد، تقاضا بیشتر خواهد بود؛ و هر چقدر قیمت بیشتر باشد، تقاضا کمتر خواهد بود. شما فکر می کنید که تعداد خریداری شده باید تابعی از قیمت باشد ـــ قیمت را به آن وارد کنید و کشف کنید که افراد چندین محصول با آن قیمت می توانند خریداری کنند ـــ اما به طور سنتی یک تابع تقاضا برخلاف این نوشته می شود. قیمت به صورت تابعی از تعداد مورد نیاز بیان می شود. من می دانم که این اندکی عجیب به نظر می آید، اما نگران نباشید ـــ این تابع در هر دو جهت کار می کند. به آن اینگونه فکر کنید: اگر یک خرده فروش بخواهد تعداد خاصی از یک محصول را بفروشد، تابع تقاضا به آن خرده فروش می گوید که قیمت فروش را چگونه باید تنظیم کند.
اوکی، در اینجا مثالی داریم. یک تولید کننده تابع تقاضا را برای چیزهایی که تولید می کند، اینگونه مشخص ساخته است:
$$p=\frac{1000}{\sqrt{x}}$$
در این تابع \(p\) قیمت محصول تولیدی و \(x\) تعداد چیزهای مورد نیاز است. بهای تولید \(x\) محصول با تابع هزینۀ زیر تعیین می شود:
$$C(x)=10x+100 \sqrt{x} + 10,000$$
هزینۀ نهایی، درآمد نهایی، و سود نهایی را در \(x=100\) تعیین کنید. همچنین، اینکه چند محصول باید تولید شود، و اینکه برای تولید بیشترین سود، به چه قیمتی باید فروخته شوند، و اینکه ماکزیمم سود چیست؟
هزینۀ نهایی (Marginal cost)
هزینۀ نهایی مشتق تابع هزینه می باشد، بنابراین مشتق آن را بگیرید و آن را در \(x=100\) ارزیابی کنید:
$$C(x)=10x+100\sqrt{x}+10,000 \\
C'(x)=10+\frac{50}{\sqrt{x}} \\
C'(100)=10+\frac{50}{\sqrt{100}} \\
=10+\frac{50}{10} \\
=15
$$
بنابراین، هزینۀ نهایی در \(x=100\) برابر با \($15\) می باشد ـــ این هزینۀ تقریبی برای تولید محصول \(101\)ام می باشد.
درآمد نهایی (Marginal revenue)
درآمد، \(R(x)\)، برابر با تعداد آیتم های فروخته شده، \(x\)، ضربدر قیمت، \(p\)، می باشد:
$$R(x)=x \cdot p \\
= x \cdot \frac{1000}{\sqrt{x}} \\
= \frac{1000x}{\sqrt{x}} \cdot \frac{\sqrt{x}}{\sqrt{x}} \\
=\frac{1000x \sqrt{x}}{x} \\
=1000\sqrt{x}$$
درآمد نهایی برابر با مشتق تابع درآمد می باشد، بنابراین مشتق \(R(x)\) را بگیرید و آن را در \(x=100\) ارزیابی کنید:
$$R(x)=1000 \sqrt{x} \\
R'(x) = \frac{500}{\sqrt{x}} \\
R'(100) = \frac{500}{\sqrt{100}} \\
= 50$$
بنابراین، درآمد تقریبی از فروش \(101\)امین محصول برابر با \($50\) می باشد.
سود نهایی (Marginal profit)
سود، \(P(x)\)، برابر با درآمد منهای هزینه می باشد. بنابراین:
$$P(x)=R(x)-C(x) \\
=1000 \sqrt{x} - (10x + 100\sqrt{x} + 10,000) \\
= -10 x+900\sqrt{x}-10,000$$
سود نهایی برابر با مشتق تابع سود می باشد، بنابراین مشتق \(P(x)\) را بگیرید، و آن را در \(x=100\) ارزیابی کنید:
$$P(x)=-10x+900\sqrt{x}-10,000 \\
P'(x)=-10+\frac{450}{\sqrt{x}} \\
P'(100)=-10+\frac{450}{\sqrt{100}} \\
=-10+45 \\
=35$$
فروش \(101\)امین محصول، سود تقریبی \($35\) دلار را به همراه دارد.
میان برهای سود نهایی: آیا متوجه هر کدام از دو میان بری که می توانید در اینجا استفاده کنید، شده اید؟ ابتدا شما می توانید از واقعیت زیر، برای تعیین مستقیم \(P'(x)\)، بدون اینکه ابتد \(P(x)\) را تعیین کنید، استفاده کنید. سپس بعد از اینکه \(P'(x)\) را بدست آوردید، صرفاً \(100\) را برای رسیدن به پاسخ در \(x\) جایگذاری کنید.
$$P'(x)=R'(x)-C'(x)$$
و اگر تمام چیزی که شما می خواهید اینست که \(P'(100)\) را تعیین کنید، می توانید از میان بر واقعاً کوتاه زیر استفاده کنید:
$$P'(100)=R'(100)-C'(100) \\
=50-15 \\
=35$$
$$P'(x)=R'(x)-C'(x)$$
و اگر تمام چیزی که شما می خواهید اینست که \(P'(100)\) را تعیین کنید، می توانید از میان بر واقعاً کوتاه زیر استفاده کنید:
$$P'(100)=R'(100)-C'(100) \\
=50-15 \\
=35$$
این یک چیز بدیهی است. اگر تولید \(101\)امین محصول برای شما در حدود \($15\) هزینه بردارد، و شما آن را در حدود \($50\) بفروشید، سپس سود شما در حدود \($35\) خواهد بود.
من این کار را با روش طولانی تر انجام دادم زیرا برای مسالۀ زیر، شما به هر دو تابعِ سود، \(P(x)\)، و سود نهایی، \(P'(x)\)، نیاز خواهید داشت.
ماکزیمم سود (Maximum profit)
برای تعیین ماکزیمم سود، مشتق سود را ـــ که سود نهایی می باشد ـــ برابر با صفر قرار دهید، آن را برای بدست آوردن \(x\) حل کنید، و سپس نتیجه را در تابع سود، جایگذاری کنید:
$$P'(x)=-10+\frac{450}{\sqrt{x}} \\
0=-10+\frac{450}{\sqrt{x}} \\
10=\frac{450}{\sqrt{x}} \\
10\sqrt{x}=450 \\
\sqrt{x}=45 \\
x=2025$$
بنابراین، ماکزیمم سود زمانی رخ می دهد که \(2,025\) محصول فروخته شود. آن را در \(P(x)\) جایگذاری کنید:
$$P(x)=-10x+900\sqrt{x}-10,000 \\
P(2025)=-10 \cdot 2025 + 900 \sqrt{2025} - 10,000 \\
=-20,250 + 900 \cdot 45 - 10,000 \\
=10,250$$
بدین ترتیب، ماکزیمم سود برابر با \($10,250\) می باشد.
آیا متوجه شدید که من در کجای این مسأله کمی تنبل شدم؟ مشتق تابع سود در \(x=2025\) برابر با صفر می باشد، اما این تضمین نمی کند که در آن مقدار \(x\) یک ماکزیمم وجود داشته باشد. ممکن است در آنجا یک مینیمم یا یک نقطۀ عطف باشد. شما می توانید از آزمون مشتق اول یا آزمون مشتق دوم (فصل 11 را ببینید) استفاده کنید تا نشان دهید که آن واقعاً یک ماکزیمم است. اما من صرفاً نگاهی به نمودار تابع سود انداختم و دیدم که آن به نوعی به شکل یک فنجان وارونه است، بنابراین دانستم که در \(x=2025\) یک ماکزیمم وجود دارد.
در پایان، تعداد فروخته شده را در تابع تقاضا جایگذاری کنید، تا بهای ماکزیمم سود را بدست آورید:
$$p=\frac{1000}{\sqrt{x}} \\
p=\frac{1000}{\sqrt{2025}} \\
\approx 22.22$$
بنابراین ماکزیمم سود \($10,250\) زمانی رخ می دهد که قیمت برابر با \($22.22\) باشد. در این قیمت، \(2,025\) محصول فروخته خواهد شد. شکل 6-13 این نتایج را خلاصه کرده است. توجه داشته باشید از آنجاییکه سود برابر با درآمد منهای هزینه می باشد، مسافت عمودی یا شکاف بین درآمد و هزینه در یک مقدار \(x\) مشخص، سود در آن مقدار \(x\) را نتیجه می دهد. ماکزیمم سود زمانی رخ می دهد که این شکاف در بالاترین حد ممکنش باشد.

و در اینجا چیز دیگری داریم. از آنجا که ماکزیمم سود در جایی رخ می دهد که \(P'(x)=0\)، و از آنجا که \(P'(x)=R'(x)-C'(x)\)، نتیجه این می شود که این سود در \(0=R'(x)-C'(x)\) در بالاترین حد ممکنش می باشد ـــ به عبارت دیگر، \(R'(x)=C'(x)\). و هنگامی که \(R'(x)=C'(x)\)، شیب خط های مماس این توابع برابر می باشند. بنابراین، اگر قرار باشد تا خط های مماسی را برای \(R(x)\) و \(C(x)\) ترسیم کنید که شکاف بین آنها در بالاترین حد باشد، این خط های مماس با یکدیگر موازی خواهند بود.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: