خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
تخمین مساحت (Approximating Area)

قبل از آنکه چگونگی محاسبۀ مساحت دقیق را شرح دهیم، می خواهم به شما نشان دهم چگونه مساحت را تخمین بزنید. روش تقریب نه تنها به این دلیل که زمینه را برای روش دقیق ـــ انتگرال گیری ـــ آماده می کند حائز اهمیت است، بلکه در مورد برخی منحنی ها، انتگرال گیری غیرممکن است، و تقریب یک مساحت بهترین کاری است که می توانید انجام دهید.

فرض کنید مساحت دقیق زیر منحنی \(f(x)=x^2+1\) را بین \(x=0\) و \(x=3\) می خواهید. مساحت سایه دار بر روی نمودار موجود در سمت چپِ شکل 4-14 را ببینید.
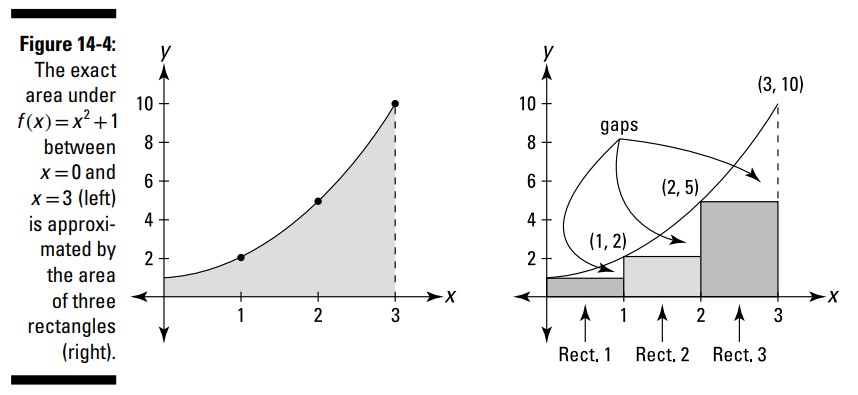
شما می توانید با کشیدن سه مستطیل زیر منحنی، همانطور که در سمت راست شکل 4-14 نشان داده شده است، و سپس جمع زدن مساحت آنها با یکدیگر، به یک برآورد حدسی از مجموع این مساحت برسید.
مستطیل های موجود در شکل 4-14 نشان دهندۀ چیزی با نام مجموع سمت چپ (left sum) می باشند زیرا ارتفاع هر مستطیل با جاییکه گوشۀ بالا و سمت چپ هر مستطیل منحنی را لمس می کند، تعیین می شود. هر مستطیل دارای عرض \(1\) می باشد و ارتفاع هر مستطیل با ارتفاع این تابع در لبۀ سمت چپ این مستطیل تعیین می شود. بنابراین، مستطیل شمارۀ 1 دارای ارتفاع \(f(0)=0^2+1=1\) می باشد؛ بدین ترتیب مساحت آن (طول ضربدر عرض یا ارتفاع ضربدر عرض) برابر با \(1 \cdot 1 = 1\) می باشد. ارتفاع مستطیل شمارۀ 2 برابر با \(f(2)=1^2+1=2\) می باشد، پس مساحت آن \(2 \cdot 1 = 2\) می باشد. و مستطیل 3 دارای ارتفاع \(f(2)=2^2+1=5\) می باشد، بنابراین مساحتش برابر با \(5 \cdot 1 = 5\) است. با جمع کردن این سه مساحت به \(1+2+5=8\) می رسید. شما می توانید ببینید که این یک تخمین کم (underestimate) از مجموع مساحت زیر این منحنی می باشد زیرا سه شکاف موجود در این مستطیل ها و منحنی موجود در شکل 4-14 این موضوع را به شما نشان می دهد.
برای یک تخمین بهتر، تعداد این مستطیل ها را دوبرابر کرده و به شش برسانید. شکل 5-14 شش مستطیل را زیر این منحنی نشان می دهد و همچنین نشان می دهد که چگونه این شش مستطیل شروع به پر کردن شکافهای موجود در شکل 4-14 کرده اند.
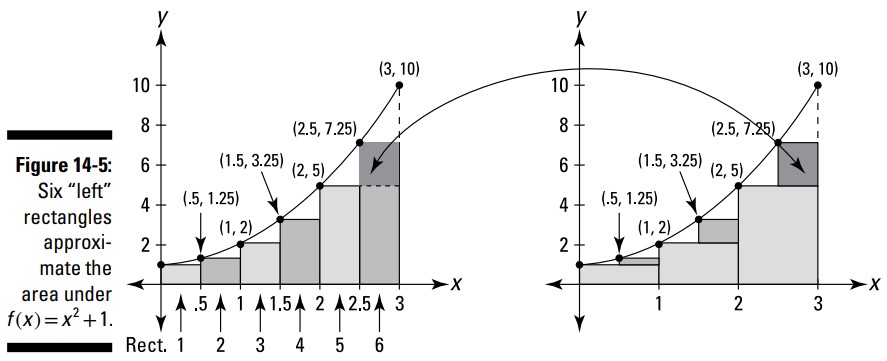
آیا آن سه مستطیل کوچکِ سایه دار در نمودار سمت راست از شکل 5-14 را می بینید؟ آنها در بالای سه مستطیل موجود در شکل 4-14 قرار گرفته اند و نشان می دهند که چگونه تخمین مساحت با استفاده از شش مستطیل به جای سه مستطیل، بهبود یافته است.
اکنون مساحت این شش مستطیل را با یکدیگر جمع بزنید. هر کدام از آنها دارای عرض \(0.5\) می باشد و ارتفاع های آنها برابر با \(f(0), f(0.5), f(1), f(1.5),...\) و به همین ترتیب می باشند. من شما را با حساب نمی آزارم. مجموع اینست: \(0.5+0.625+1+1.625+2.5+3.625=9.875\) . این یک تخمین بهتر است، اما هنوز هم یک تخمین کم (underestimate) است و دلیل آنهم شش شکاف کوچکی است که می توانید در نمودار سمت چپ از شکل 5-14 ببینید.
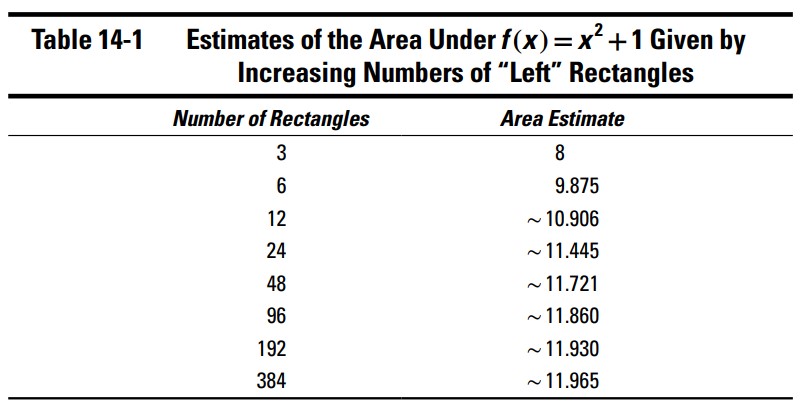
جدول 1-14 تخمین های مسافت بدست آمده با استفاده از \(3, 6, 12, 24, 48, 96, 192\) و \(384\) مستطیل را نشان می دهد. شما مجبور نیستید مانند کاری که من کردم، هربار تعداد مستطیل ها را دوبرابر کنید. شما می توانید به هر تعداد مستطیل با عرض برابر که بخواهید، مورد استفاده قرار دهید. من به این دلیل طرح دوبرابر کردن را دوست دارم که با هر دوبرابر کردن، شکاف ها با روشی که در شکل 5-14 نشان دادم، بیشتر و بیشتر پُر می شوند. آیا می توانید حدس بزنید که این تخمین ها در جدول 1-14 به کدام سمت می روند؟ به نظر می رسد حدس من \(12\) باشد.
در اینجا فرمول فانتزی برای جمع مستطیل های چپ (left-rectangle sum) را می بینید:
بهتر است این فرمول را اندکی توضیح دهم. به شش مستطیلی که در شکل 5-14 نشان دادیم، بازگردید. عرض هر کدام از این مستطیل ها برابر با کل طول از \(0\) تا \(3\) (که مسلماً برابر با \(3-0=3\) می باشد) تقسیم بر تعداد این مستطیل ها، یعنی \(6\)، می باشد. این چیزی است که \(\frac{b-a}{n}\) در این فرمول می گوید.
حالا، در مورد آن \(x\)های دارای زیرنویس چطور؟ مختصات \(x\) از لبۀ سمت چپ مستطیل 1 در شکل 5-14 را \(x_0\) می نامیم، سمت راست مستطیل 1 (که با سمت چپ مستطیل دوم یکسان است) در \(x_1\) می باشد، سمت راست مستطیل 2 در \(x_2\) می باشد، سمت راست مستطیل 3 در \(x_3\) می باشد، و به همین ترتیب تمام این مسیر تا سمت راست مستطیل 6، که در \(x_6\) می باشد، ادامه می یابد. برای این شش مستطیلِ موجود در شکل 5-14، \(x_0\) برابر با \(0\)، \(x_1\) برابر با \(0.5\)، \(x_2\) برابر با \(1\)، \(x_3\) برابر با \(1.5\)، \(x_4\) برابر با \(2\)، \(x_5\) برابر با \(2.5\)، و \(x_6\) برابر با \(3\) می باشد. ارتفاع های این شش مستطیل چپ در شکل 5-14 در لبۀ سمت چپ آنها، که از \(x_0\) تا \(x_5\) می باشند، رخ می دهند. در یک جمع سمت چپ، شما از لبۀ سمت راست آخرین مستطیل، \(x_6\)، استفاده نمی کنید. به همین دلیل است که لیست مقادیر این توابع در این فرمول در \(x_{n-1}\) متوقف می شود. هنگامی که به فرمول مستطیل های راست در بخش بعدی همین فصل برسید، این برای شما واضح تر می گردد.
در اینجا چگونگی استفاده از این فرمول برای شش مستطیل موجود در شکل 5-14 را می بینید:
$$L_6=\frac{3-0}{6}[f(x_0)+f(x_1)+f(x_2)+f(x-3)+f(x_4)+f(x_5)] \\
=\frac{1}{2}[f(0)+f(0.5)+f(1)+f(1.5)+f(2)+f(2.5)] \\
=\frac{1}{2}[1+1.25+2+3.25+5+7.25] \\
=\frac{1}{2}(19.75) \\
=9.875
$$
توجه داشته باشید که اگر من عرض \(\frac{1}{2}\) را بعد از خط سوم بر روی هر کدام از جملات داخل پرانتز توزیع کنم (ضرب کنم)، شما مساحت جداگانۀ هر کدام از مستطیل ها را که پیشتر در دو پاراگراف بعد از شکل 5-14 دیده بودید، خواهید دید. این فرمول صرفاً از یک میانبر استفاده می کند که ابتدا ارتفاع ها را با یکدیگر جمع می کند و سپس آنها را در عرض ضرب می کند.
اکنون همان مساحت زیر \(f(x)=x^2+1\) از \(0\) تا \(3\) را با مستطیل های راست (right rectangles) تخمین بزنید. این روش مشابه روش مجموع چپ عمل می کند با این استثناء که هر مستطیل به نحوی ترسیم می شود که گوشۀ بالا و سمت راست آن، منحنی را لمس کند. شکل 6-14 را ببینید.
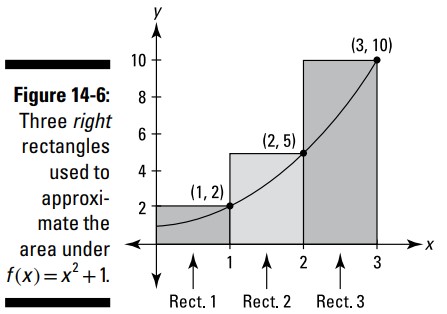
ارتفاع های سه مثلث موجود در شکل 6-14 با مقادیر تابع در لبه های راست آنها بدست می آیند: \(f(1)=2\)، \(f(2)=5\)، و \(f(3)=10\). هر مستطیل دارای عرض \(1\) می باشد، بنابراین مساحتها عبارت از \(2\)، \(5\)، و \(10\) می باشند، که مجموعشان \(17\) می شود. همانطور که می بینید، برخلاف تخمین کم که در روش مستطیل چپ بود، این بار به یک تخمین بالا (overestimate) برای مساحت واقعی زیر منحنی رسیده اید. جدول 2-14 تخمین های بهبود یافته را با روش مستطیل راست به شما نشان می دهد.
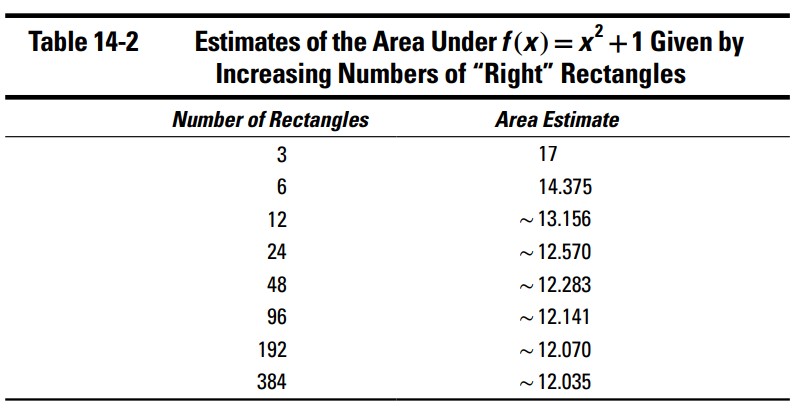
به نظر می رسد این تخمین ها نیز بسوی 12 می روند. در اینجا فرمولی برای یک مجموع مستطیل راست را می بینید.
اگر این فرمول را با فرمول مجموع مستطیل چپ مقایسه کنید، به تصویر کاملی از آن زیرنویس ها می رسید. این دو فرمول یکسانند به استثناء یک چیز. به مجموع مقادیر توابع در هر دو فرمول بنگرید. فرمول جمع راست داری مقداری است، \(f(x_n)\)، که فرمول جمع چپ، فاقد آن می باشد، و فرمول سمت چپ دارای مقداری است، \(f(x_0)\)، که فرمول جمع راست، فاقد آن می باشد. تمامی مقادیر توابع بین این دو، در هر دو فرمول ظاهر می شوند. شما با مقایسۀ سه مستطیل چپ در شکل 4-14 با سه مستطیل راست در شکل 6-14 ، می توانید درک بهتری از این مسأله پیدا کنید. مساحت ها و مجموع آنها، که پیشتر محاسبه کردیم، بدین قرار می باشند:
$$\text{Three left rectangles: } 1+2+5=8 \\
\text{Three right rectangles: } 2+5+10=17$$
مقادیر مورد استفاده در این مجموع مساحتها، به این استثناء مستطیل قرار گرفته در منتهی الیه سمت چپ از مستطیل های چپ و مستطیل قرار گرفته در منتهی الیه سمت راست از مستطیل های راست، یکسانند. هر دو مجموع شامل مستطیل هایی با مساحت های \(2\) و \(5\) می باشند. اگر به ساختار مستطیل ها دقت کنید، متوجه خواهید شد که دومین و سومین مستطیل در شکل 4-14 با اولین و دومین مستطیل در شکل 6-14 یکسان می باشند.
یک روش سوم برای تقریب مساحتها با مستطیل ها اینست که کاری کنیم هر مستطیل در نقطۀ میانی ضلع بالایی اش از منحنی عبور کند. یک جمع نقطۀ میانی (midpoint sum) معمولاً تخمین خیلی بهتری از مساحتی که با جمع راست یا جمع چپ بدست آمده است، می باشد. شکل 7-14 نشان می دهد چرا اینگونه است.
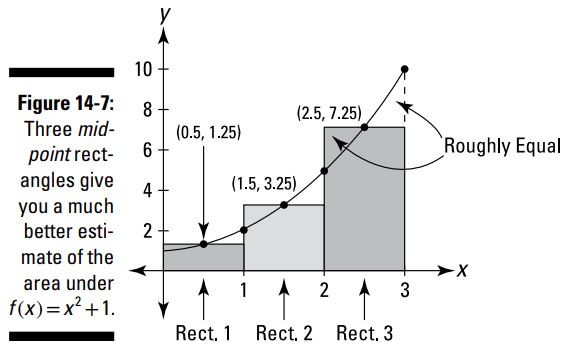
در شکل 7-14 می توانید ببینید که بخشی از هر مستطیل که بالای منحنی قرار دارد، تقریباً با شکاف بین مستطیل و منحنی یکسان به نظر می آید. دلیل اینکه یک مجموع نقطۀ میانی، تخمین بهتری را ایجاد می کند، اینست که این دو خطا تقریباً همدیگر را خنثی می کنند.
برای سه مستطیل موجود در شکل 7-14 ، عرض ها برابر با \(1\) و ارتفاع ها برابر با \(f(0.5)=1.25\)، \(f(1.5)=3.25\)، و \(f(2.5)=7.25\) می باشند. مجموع مساحت ها برابر با \(11.75\) می باشد. جدول 3-14 جمع نقاط میانی برای تعداد یکسانی مستطیل که در جدول های 1-14 و 2-14 مورد استفاده قرار گرفته بودند را نشان می دهد.
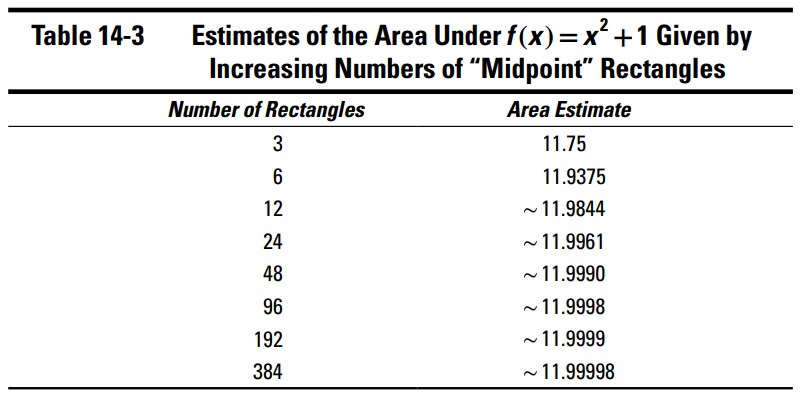
اگر در اینکه جمع های راست و چپ در جداول 1-14 و 2-14 به سوی 12 می رفتند، هر گونه شکی داشتید، جدول 3-14 شک شما را از بین می برد. بله، در واقع مساحت دقیق برابر با \(12\) می باشد. (در ادامۀ این فصل چگونگی محاسبۀ آن را به شما نشان خواهم داد.) و برای اینکه ببینید تقریب نقطۀ میانی، نسبت به تقریب راست و تقریب چپ، چقدر سریعتر به پاسخ دقیق \(12\) نزدیک می شود، این سه جدول را با یکدیگر مقایسه کنید. خطای موجود با \(6\) مستطیل در نقطۀ میانی در حدود خطای مشابه با \(192\) مستطیل در روش راست یا چپ می باشد!
جمع های چپ، راست، و نقطۀ میانی در جدول های 1-14، 2-14، و 3-14 همگی بسوی \(12\) پیش می روند، و اگر بتوانید این مساحت را به بی نهایت مستطیل تقسیم کنید، به مساحت دقیق \(12\) می رسید.

تقریب مساحت با مجموع سمت چپ (left sums)
فرض کنید مساحت دقیق زیر منحنی \(f(x)=x^2+1\) را بین \(x=0\) و \(x=3\) می خواهید. مساحت سایه دار بر روی نمودار موجود در سمت چپِ شکل 4-14 را ببینید.

شما می توانید با کشیدن سه مستطیل زیر منحنی، همانطور که در سمت راست شکل 4-14 نشان داده شده است، و سپس جمع زدن مساحت آنها با یکدیگر، به یک برآورد حدسی از مجموع این مساحت برسید.
مستطیل های موجود در شکل 4-14 نشان دهندۀ چیزی با نام مجموع سمت چپ (left sum) می باشند زیرا ارتفاع هر مستطیل با جاییکه گوشۀ بالا و سمت چپ هر مستطیل منحنی را لمس می کند، تعیین می شود. هر مستطیل دارای عرض \(1\) می باشد و ارتفاع هر مستطیل با ارتفاع این تابع در لبۀ سمت چپ این مستطیل تعیین می شود. بنابراین، مستطیل شمارۀ 1 دارای ارتفاع \(f(0)=0^2+1=1\) می باشد؛ بدین ترتیب مساحت آن (طول ضربدر عرض یا ارتفاع ضربدر عرض) برابر با \(1 \cdot 1 = 1\) می باشد. ارتفاع مستطیل شمارۀ 2 برابر با \(f(2)=1^2+1=2\) می باشد، پس مساحت آن \(2 \cdot 1 = 2\) می باشد. و مستطیل 3 دارای ارتفاع \(f(2)=2^2+1=5\) می باشد، بنابراین مساحتش برابر با \(5 \cdot 1 = 5\) است. با جمع کردن این سه مساحت به \(1+2+5=8\) می رسید. شما می توانید ببینید که این یک تخمین کم (underestimate) از مجموع مساحت زیر این منحنی می باشد زیرا سه شکاف موجود در این مستطیل ها و منحنی موجود در شکل 4-14 این موضوع را به شما نشان می دهد.
برای یک تخمین بهتر، تعداد این مستطیل ها را دوبرابر کرده و به شش برسانید. شکل 5-14 شش مستطیل را زیر این منحنی نشان می دهد و همچنین نشان می دهد که چگونه این شش مستطیل شروع به پر کردن شکافهای موجود در شکل 4-14 کرده اند.

آیا آن سه مستطیل کوچکِ سایه دار در نمودار سمت راست از شکل 5-14 را می بینید؟ آنها در بالای سه مستطیل موجود در شکل 4-14 قرار گرفته اند و نشان می دهند که چگونه تخمین مساحت با استفاده از شش مستطیل به جای سه مستطیل، بهبود یافته است.
اکنون مساحت این شش مستطیل را با یکدیگر جمع بزنید. هر کدام از آنها دارای عرض \(0.5\) می باشد و ارتفاع های آنها برابر با \(f(0), f(0.5), f(1), f(1.5),...\) و به همین ترتیب می باشند. من شما را با حساب نمی آزارم. مجموع اینست: \(0.5+0.625+1+1.625+2.5+3.625=9.875\) . این یک تخمین بهتر است، اما هنوز هم یک تخمین کم (underestimate) است و دلیل آنهم شش شکاف کوچکی است که می توانید در نمودار سمت چپ از شکل 5-14 ببینید.
جدول 1-14 تخمین های مسافت بدست آمده با استفاده از \(3, 6, 12, 24, 48, 96, 192\) و \(384\) مستطیل را نشان می دهد. شما مجبور نیستید مانند کاری که من کردم، هربار تعداد مستطیل ها را دوبرابر کنید. شما می توانید به هر تعداد مستطیل با عرض برابر که بخواهید، مورد استفاده قرار دهید. من به این دلیل طرح دوبرابر کردن را دوست دارم که با هر دوبرابر کردن، شکاف ها با روشی که در شکل 5-14 نشان دادم، بیشتر و بیشتر پُر می شوند. آیا می توانید حدس بزنید که این تخمین ها در جدول 1-14 به کدام سمت می روند؟ به نظر می رسد حدس من \(12\) باشد.

در اینجا فرمول فانتزی برای جمع مستطیل های چپ (left-rectangle sum) را می بینید:
قانون مستطیل چپ (left rectangle rule): شما می توانید مساحت دقیق زیر یک منحنی، بین \(a\) و \(b\) ، یعنی \(\int_a^b f(x)dx\)، را با مجموع مستطیل های چپ با عرض برابر، با استفاده از فرمول زیر تخمین بزنید. در حالت کلی، هر چه تعداد این مستطیل ها بیشتر باشد، تخمین بهتر خواهد بود.
$$L_n = \frac{b-a}{n} [f(x_0)+f(x_1)+f(x_2)+..........+f(x_{n-1})],$$
در این فرمول \(n\) برابر با تعداد مستطیل ها، \(\frac{b-a}{n}\) برابر با عرض هر مستطیل، \(x_0\) تا \(x_{n-1}\) برابر با مختصات های \(x\) لبه های چپ از این \(n\) مستطیل، و مقادیر تابع برابر با ارتفاع این مستطیل ها، می باشند.
$$L_n = \frac{b-a}{n} [f(x_0)+f(x_1)+f(x_2)+..........+f(x_{n-1})],$$
در این فرمول \(n\) برابر با تعداد مستطیل ها، \(\frac{b-a}{n}\) برابر با عرض هر مستطیل، \(x_0\) تا \(x_{n-1}\) برابر با مختصات های \(x\) لبه های چپ از این \(n\) مستطیل، و مقادیر تابع برابر با ارتفاع این مستطیل ها، می باشند.
بهتر است این فرمول را اندکی توضیح دهم. به شش مستطیلی که در شکل 5-14 نشان دادیم، بازگردید. عرض هر کدام از این مستطیل ها برابر با کل طول از \(0\) تا \(3\) (که مسلماً برابر با \(3-0=3\) می باشد) تقسیم بر تعداد این مستطیل ها، یعنی \(6\)، می باشد. این چیزی است که \(\frac{b-a}{n}\) در این فرمول می گوید.
حالا، در مورد آن \(x\)های دارای زیرنویس چطور؟ مختصات \(x\) از لبۀ سمت چپ مستطیل 1 در شکل 5-14 را \(x_0\) می نامیم، سمت راست مستطیل 1 (که با سمت چپ مستطیل دوم یکسان است) در \(x_1\) می باشد، سمت راست مستطیل 2 در \(x_2\) می باشد، سمت راست مستطیل 3 در \(x_3\) می باشد، و به همین ترتیب تمام این مسیر تا سمت راست مستطیل 6، که در \(x_6\) می باشد، ادامه می یابد. برای این شش مستطیلِ موجود در شکل 5-14، \(x_0\) برابر با \(0\)، \(x_1\) برابر با \(0.5\)، \(x_2\) برابر با \(1\)، \(x_3\) برابر با \(1.5\)، \(x_4\) برابر با \(2\)، \(x_5\) برابر با \(2.5\)، و \(x_6\) برابر با \(3\) می باشد. ارتفاع های این شش مستطیل چپ در شکل 5-14 در لبۀ سمت چپ آنها، که از \(x_0\) تا \(x_5\) می باشند، رخ می دهند. در یک جمع سمت چپ، شما از لبۀ سمت راست آخرین مستطیل، \(x_6\)، استفاده نمی کنید. به همین دلیل است که لیست مقادیر این توابع در این فرمول در \(x_{n-1}\) متوقف می شود. هنگامی که به فرمول مستطیل های راست در بخش بعدی همین فصل برسید، این برای شما واضح تر می گردد.
در اینجا چگونگی استفاده از این فرمول برای شش مستطیل موجود در شکل 5-14 را می بینید:
$$L_6=\frac{3-0}{6}[f(x_0)+f(x_1)+f(x_2)+f(x-3)+f(x_4)+f(x_5)] \\
=\frac{1}{2}[f(0)+f(0.5)+f(1)+f(1.5)+f(2)+f(2.5)] \\
=\frac{1}{2}[1+1.25+2+3.25+5+7.25] \\
=\frac{1}{2}(19.75) \\
=9.875
$$
توجه داشته باشید که اگر من عرض \(\frac{1}{2}\) را بعد از خط سوم بر روی هر کدام از جملات داخل پرانتز توزیع کنم (ضرب کنم)، شما مساحت جداگانۀ هر کدام از مستطیل ها را که پیشتر در دو پاراگراف بعد از شکل 5-14 دیده بودید، خواهید دید. این فرمول صرفاً از یک میانبر استفاده می کند که ابتدا ارتفاع ها را با یکدیگر جمع می کند و سپس آنها را در عرض ضرب می کند.
تقریب مساحت با مجموع راست (right sums)
اکنون همان مساحت زیر \(f(x)=x^2+1\) از \(0\) تا \(3\) را با مستطیل های راست (right rectangles) تخمین بزنید. این روش مشابه روش مجموع چپ عمل می کند با این استثناء که هر مستطیل به نحوی ترسیم می شود که گوشۀ بالا و سمت راست آن، منحنی را لمس کند. شکل 6-14 را ببینید.

ارتفاع های سه مثلث موجود در شکل 6-14 با مقادیر تابع در لبه های راست آنها بدست می آیند: \(f(1)=2\)، \(f(2)=5\)، و \(f(3)=10\). هر مستطیل دارای عرض \(1\) می باشد، بنابراین مساحتها عبارت از \(2\)، \(5\)، و \(10\) می باشند، که مجموعشان \(17\) می شود. همانطور که می بینید، برخلاف تخمین کم که در روش مستطیل چپ بود، این بار به یک تخمین بالا (overestimate) برای مساحت واقعی زیر منحنی رسیده اید. جدول 2-14 تخمین های بهبود یافته را با روش مستطیل راست به شما نشان می دهد.

به نظر می رسد این تخمین ها نیز بسوی 12 می روند. در اینجا فرمولی برای یک مجموع مستطیل راست را می بینید.
قانون مستطیل راست (right rectangle rule): شما می توانید مساحت دقیق زیر یک منحنی بین \(a\) و \(b\)، یعنی \(\int_a^b f(x)dx\)، را با مجموع مستطیل های راست با استفاده از فرمول زیر بدست آورید. در حالت کلی، هرچقدر مستطیل ها بیشتر باشند، تخمین بهتر خواهد بود.
$$R_n=\frac{b-a}{n}[f(x_1)+f(x_2)+f(x_3)+..........+f(x_n)],$$
در این فرمول، \(n\) تعداد مستطیل ها، \(\frac{b-a}{n}\) عرض هر مستطیل، \(x_1\) تا \(x_n\) مختصات های \(x\) از لبه های راست این \(n\) مستطیل، و مقادیر توابع برابر با ارتفاع های این مستطیل ها می باشند.
$$R_n=\frac{b-a}{n}[f(x_1)+f(x_2)+f(x_3)+..........+f(x_n)],$$
در این فرمول، \(n\) تعداد مستطیل ها، \(\frac{b-a}{n}\) عرض هر مستطیل، \(x_1\) تا \(x_n\) مختصات های \(x\) از لبه های راست این \(n\) مستطیل، و مقادیر توابع برابر با ارتفاع های این مستطیل ها می باشند.
اگر این فرمول را با فرمول مجموع مستطیل چپ مقایسه کنید، به تصویر کاملی از آن زیرنویس ها می رسید. این دو فرمول یکسانند به استثناء یک چیز. به مجموع مقادیر توابع در هر دو فرمول بنگرید. فرمول جمع راست داری مقداری است، \(f(x_n)\)، که فرمول جمع چپ، فاقد آن می باشد، و فرمول سمت چپ دارای مقداری است، \(f(x_0)\)، که فرمول جمع راست، فاقد آن می باشد. تمامی مقادیر توابع بین این دو، در هر دو فرمول ظاهر می شوند. شما با مقایسۀ سه مستطیل چپ در شکل 4-14 با سه مستطیل راست در شکل 6-14 ، می توانید درک بهتری از این مسأله پیدا کنید. مساحت ها و مجموع آنها، که پیشتر محاسبه کردیم، بدین قرار می باشند:
$$\text{Three left rectangles: } 1+2+5=8 \\
\text{Three right rectangles: } 2+5+10=17$$
مقادیر مورد استفاده در این مجموع مساحتها، به این استثناء مستطیل قرار گرفته در منتهی الیه سمت چپ از مستطیل های چپ و مستطیل قرار گرفته در منتهی الیه سمت راست از مستطیل های راست، یکسانند. هر دو مجموع شامل مستطیل هایی با مساحت های \(2\) و \(5\) می باشند. اگر به ساختار مستطیل ها دقت کنید، متوجه خواهید شد که دومین و سومین مستطیل در شکل 4-14 با اولین و دومین مستطیل در شکل 6-14 یکسان می باشند.
تقریب مساحت با مجموع نقطه میانی (midpoint sums)
یک روش سوم برای تقریب مساحتها با مستطیل ها اینست که کاری کنیم هر مستطیل در نقطۀ میانی ضلع بالایی اش از منحنی عبور کند. یک جمع نقطۀ میانی (midpoint sum) معمولاً تخمین خیلی بهتری از مساحتی که با جمع راست یا جمع چپ بدست آمده است، می باشد. شکل 7-14 نشان می دهد چرا اینگونه است.

در شکل 7-14 می توانید ببینید که بخشی از هر مستطیل که بالای منحنی قرار دارد، تقریباً با شکاف بین مستطیل و منحنی یکسان به نظر می آید. دلیل اینکه یک مجموع نقطۀ میانی، تخمین بهتری را ایجاد می کند، اینست که این دو خطا تقریباً همدیگر را خنثی می کنند.
برای سه مستطیل موجود در شکل 7-14 ، عرض ها برابر با \(1\) و ارتفاع ها برابر با \(f(0.5)=1.25\)، \(f(1.5)=3.25\)، و \(f(2.5)=7.25\) می باشند. مجموع مساحت ها برابر با \(11.75\) می باشد. جدول 3-14 جمع نقاط میانی برای تعداد یکسانی مستطیل که در جدول های 1-14 و 2-14 مورد استفاده قرار گرفته بودند را نشان می دهد.

اگر در اینکه جمع های راست و چپ در جداول 1-14 و 2-14 به سوی 12 می رفتند، هر گونه شکی داشتید، جدول 3-14 شک شما را از بین می برد. بله، در واقع مساحت دقیق برابر با \(12\) می باشد. (در ادامۀ این فصل چگونگی محاسبۀ آن را به شما نشان خواهم داد.) و برای اینکه ببینید تقریب نقطۀ میانی، نسبت به تقریب راست و تقریب چپ، چقدر سریعتر به پاسخ دقیق \(12\) نزدیک می شود، این سه جدول را با یکدیگر مقایسه کنید. خطای موجود با \(6\) مستطیل در نقطۀ میانی در حدود خطای مشابه با \(192\) مستطیل در روش راست یا چپ می باشد!
قانون نقطۀ میانی (midpoint rule): شما می توانید مساحت دقیق زیر یک منحنی بین \(a\) و \(b\)، یعنی \(\int_a^b f(x)dx\)، با مجموع مستطیل های نقطۀ میانی (midpoint rectangles) با استفاده از فرمول زیر بدست آورید. در حالت کلی، هرچقدر تعداد مستطیل ها بیشتر باشد، تخمین بهتر خواهد بود.
$$M_n=\frac{b-a}{n} [f(\frac{x_0+x_1}{2})+f(\frac{x_1+x_2}{2})+f(\frac{x_2+x_3}{2}) +..........+f(\frac{x_{n-1}+x_{n}}{2}) ],$$
در این فرمول \(n\) تعداد مستطیل ها، \(\frac{b-a}{n}\) عرض هر مستطیل، \(x_0\) تا \(x_n\) برابر با \(n+1\) نقطه از \(a\) تا \(b\) که مساوی تقسیم شده اند، و مقادیر توابع برابر با ارتفاع های این مستطیل ها می باشند.
$$M_n=\frac{b-a}{n} [f(\frac{x_0+x_1}{2})+f(\frac{x_1+x_2}{2})+f(\frac{x_2+x_3}{2}) +..........+f(\frac{x_{n-1}+x_{n}}{2}) ],$$
در این فرمول \(n\) تعداد مستطیل ها، \(\frac{b-a}{n}\) عرض هر مستطیل، \(x_0\) تا \(x_n\) برابر با \(n+1\) نقطه از \(a\) تا \(b\) که مساوی تقسیم شده اند، و مقادیر توابع برابر با ارتفاع های این مستطیل ها می باشند.
تعریف جمع ریمان (Riemann sum): بعد از برنارد ریمن (Bernhard Riemann) ـــ ریاضیدان بزرگ آلمانی ـــ هر سه جمع چپ، راست، و نقطۀ میانی، با نام جمع ریمان شناخته می شوند. در واقع، هر جمع تقریبی که از مستطیل ها تشکیل شده باشد یک جمع ریمان می باشد، شامل جمع عجیبی که عبارت از مستطیل های دارای عرض غیر برابرند نیز می باشد. خوشبختانه در سطح این کتاب نیازی نیست تا با آنها سر و کار داشته باشید.
جمع های چپ، راست، و نقطۀ میانی در جدول های 1-14، 2-14، و 3-14 همگی بسوی \(12\) پیش می روند، و اگر بتوانید این مساحت را به بی نهایت مستطیل تقسیم کنید، به مساحت دقیق \(12\) می رسید.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: