خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
نماد جمع بندی (Summation Notation)

قبل از اینکه به تعریف رسمی انتگرال معین (definite integral) بپردازیم ـــ آن یک ابزار باورنکردنی حسابان است که به نوعی یک مساحت را به بی نهایت مستطیل برش می دهد و از این طریق مساحت دقیق را به شما می دهد ـــ یک چیز دیگر هست که باید انجام شود: نماد جمع بندی.

برای جمع زدن سری های طولانی اعداد مانند مساحت مستطیل ها در یک جمع چپ، راست، یا نقطۀ میانی، نماد جمع بندی یا نماد سیگما (sigma notation) در دسترس است. در اینجا چگونگی کارکرد آن را می بینید. فرض کنید می خواهید \(100\) مضرب اول \(5\) را با یکدیگر جمع بزنید ـــ آن از \(5\) تا \(500\) است. شما می توانید این جمع را اینگونه بنویسید:
$$5+10+15+20+25+..........+490+495+500$$
اما با نماد سیگما (سیگما، \(\sum\)، هجدهمین حرف الفبای یونانی می باشد) این جمع بسیار متراکم تر و کارآمدتر است، و بیایید صادق باشیم، بسیار جالب به نظر می رسد:
$$\sum_{i=1}^{100} 5i$$
این نماد صرفاً به شما می گوید که \(1\) را در \(i\) در \(5i\) جایگذاری کنید، سپس \(2\) را در \(i\) در \(5i\) جایگذاری کنید، سپس \(3\)، سپس \(4\)، و به همین ترتیب، تا \(100\) ادامه بدهید. سپس نتایج را با یکدیگر جمع بزنید. بنابراین آن \(5 \cdot 1\) بعلاوۀ \(5 \cdot 2\) بعلاوۀ \(5 \cdot 3\)، و به همین ترتیب تا \(5 \cdot 100\) می باشد. این کار نتیجۀ یکسانی با نوشتن جمع به صورت طولانی دارد. در ضمن، حرف \(i\) هیچ معنای خاصی ندارد. شما می توانید این جمع را با یک \(j\)، یا هر حرف الفبای دیگری بنویسید:
$$\sum_{j=1}^{100} 5j$$
در این مثال دیگری داریم. اگر بخواهید جمع زیر را انجام دهید،
$$10^2 + 11^2 + 12^2 + .......... + 29^2 + 30^2$$
می توانید این جمع را با نماد سیگما به شکل زیر بنویسید:
$$\sum_{k=10}^{30} k^2$$
به همین سادگی.
شما می توانید از نماد سیگما برای نوشتن جمع مستطیل راست برای منحنی \(x^2+1\) که آن را مورد بررسی قرار دادیم، استفاده کنید.
فرمول جمع راست (right sum) را از بخش پیشین در همین فصل بخاطر آورید:
$$R_n=\frac{b-a}{n}[f(x_1)+f(x_2)+f(x_3)+..........+f(x_n)]$$
در اینجا همان فرمول را که با نماد سیگما نوشته شده است داریم:
$$R_n=\sum_{i=1}^n \biggl[f(x_i) \cdot \frac{b-a}{n} \biggr]$$
توجه داشته باشید که من می توانستم این فرمول را به شکل زیر نیز بنویسم که بیشتر و زیباتر انعکاس دهندۀ فرمول اصلی است، که در آن \(\frac{b-a}{n}\) در بیرون قرار گرفته است. هر دو روش خوب هستند ـــ آنها یکسانند ـــ اما انتخاب من این بوده است که \(\frac{b-a}{n}\) را در داخل قرار دهم، به نحوی که \(\sum\) در واقع جمع مستطیل ها باشد. به عبارت دیگر، با \(\frac{b-a}{n}\) در داخل، عبارت بعد از نماد \(\sum\)، یعنی \(f(x_i) \cdot \frac{b-a}{n}\)، که در آن نماد \(\sum\) به شما می گوید جمع بزنید، مساحت هر مستطیل می باشد، یعنی ارتفاع ضربدر قاعده.
$$R_n=\frac{b-a}{n} \sum_{i=1}^n f(x_i)$$
اکنون این را برای شش مستطیل راست در شکل 8-14 به کار بگیرید.
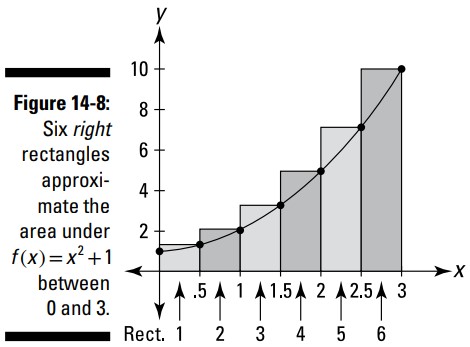
شما در حال محاسبۀ مساحت زیرِ منحنیِ \(x^2+1\) بین \(x=0\) و \(x=3\) با شش مستطیل هستید، بنابراین، عرض هر کدام برابر است با:
$$\frac{b-a}{n}=\frac{3-0}{6}=\frac{3}{6}=\frac{1}{2}$$
بنابراین خواهید داشت:
$$R_6=\sum_{i=1}^6 \biggl[f(x_i) \cdot \frac{1}{2} \biggr]$$
در ادامه، از آنجا که عرض هر مستطیل برابر با \(\frac{1}{2}\) است، لبه های راست این شش مستطیل در شش مضرب اول \(\frac{1}{2}\) قرار می گیرند: \(0.5, 1, 1.5, 2, 2.5, 3\) . این اعداد مختصات \(x\) های شش نقطۀ \(x_1\) تا \(x_6\) می باشند؛ آنها را می توانید با عبارت \(\frac{1}{2}i\) تولید کنید، که در آن \(i\) برابر با \(1\) تا \(6\) می باشد. شما می توانید با جایگذاری \(1\) برای \(i\) در \(\frac{1}{2}i\)، سپس \(2\)، سپس \(3\)، تا \(6\)، این امر را درست آزمایی کنید. اکنون می توانید \(x_i\) در این فرمول را با \(\frac{1}{2}i\) جایگذاری کنید که نتیجۀ زیر را به شما می دهد:
$$R_6=\sum_{i=1}^6 \biggl[ f \biggl( \frac{1}{2}i \biggr) \cdot \frac{1}{2} \biggr]$$
تابع ما، \(f(x)\)، برابر با \(x^2 + 1\) می باشد، بنابراین \(f(\frac{1}{2}i) = (\frac{1}{2}i)^2 + 1\)، و بنابراین می توانید بنویسید:
$$R_6=\sum_{i=1}^6 \biggl[ f \biggl( \bigl( \frac{1}{2}i \bigr)^2 + 1 \biggr) \cdot \frac{1}{2} \biggr]$$
اگر \(1\) را در \(i\) جایگذاری کنید، سپس \(2\) را، سپس \(3\)، و به همین ترتیب تا \(6\) ادامه دهید و عملیات ریاضی را انجام دهید، به جمع مساحت های مستطیل های موجود در شکل 8-14 می رسید. این نماد سیگما صرفاً یک روش فانتزی برای نوشتن جمع این شش مستطیل می باشد.
آیا مشغول تفریح هستیم؟ صبر کنید، بدتر هم می شود ـــ متاسفم. اکنون، شما می بایست شکل کلی این جمع را برای تعداد مجهول، \(n\)، مستطیل های راست، بنویسید. جمع محدودۀ مساحت در این سوال برابر با \(3\) می باشد، درست است؟ شما این محدوده را بر تعداد مستطیل ها تقسیم می کنید تا عرض هر مستطیل را بدست آورید. با \(6\) مستطیل، عرض هر کدام برابر با \(\frac{3}{6}\) می باشد؛ با \(n\) مستطیل، عرض هر کدام برابر با \(\frac{3}{n}\) می باشد. و لبۀ راست این \(n\) مستطیل با \(\frac{3}{n}i\)، برای \(i\) برابر است با \(1\) تا \(n\)، تولید می شود. این به شما نتیجۀ زیر را می دهد:
$$R_n=\sum_{i=1}^n \biggl[ f \biggl( \frac{3}{n}i \biggr) \cdot \frac{3}{n} \biggr]$$
از آنجا که \(f(x)=x^2 + 1\)، خواهیم داشت:
$$
R_n=\sum_{i=1}^n \biggl[ \biggl( \bigl( \frac{3}{n}i \bigr)^2 + 1 \biggr) \cdot \frac{3}{n} \biggr] \\
=\sum_{i=1}^n \biggl[ \biggl( \frac{9i^2}{n^2} + 1 \biggr) \cdot \frac{3}{n} \biggr] \\
=\sum_{i=1}^n \biggl[ \frac{27i^2}{n^3} + \frac{3}{n} \biggr]
$$
در مورد دو خط بعدی این عملیات فعلاً به من اعتماد کنید تا در آینده برایتان روشن شود:
$$
=\sum_{i=1}^n \frac{27i^2}{n^3} + \sum_{i=1}^n \frac{3}{n} \\
=\frac{27}{n^3} \sum_{i=1}^n i^2 + \frac{3}{n} \sum_{i=1}^n 1
$$
در آخرین مرحله، شما می توانید \(\frac{27}{n^3}\) و \(\frac{3}{n}\) را از درون نماد جمع بیرون بکشید ـــ شما اجازه دارید هر چیزی به جز تابعی از \(i\)، که به آن ایندکس جمع گفته می شود، را از آنجا بیرون بکشید. همچنین جمع دوم در مرحلۀ آخر تنها یک \(1\) بعد از آن دارد و \(i\) ندارد. بنابراین جایی برای جایگذاری مقدار \(i\) وجود ندارد. این وضعیت ممکن است اندکی عجیب به نظر آید، اما تمام کاری که شما باید انجام دهید اینست که \(n\) بار \(1\) ها را با یکدیگر جمع بزنید، که برابر با \(n\) می شود (من این کار را در زیر انجام داده ام).
شما اکنون به یک مرحلۀ حیاتی رسیده اید. با یک تردستی، شما جمع ریمان بالا را به فرمولی به لحاظ \(n\) تبدیل خواهید کرد. این فرمول چیزی است که در بخش بعدی استفاده می کنید تا مساحت دقیق زیر این منحنی را بدست آورید.
اکنون، همانطور که تقریباً هیچ کس نمی داند، جمع \(n\) مربع اول، \(1^2+2^2+3^2+..........+n^2\)، برابر است با \(\frac{n(n+1)(2n+1)}{6}\) . (راستی، این عدد \(6\) هیچ ارتباطی به این واقعیت که ما از \(6\) مستطیل در چند صفحۀ قبل استفاده کردیم ندارد.) بنابراین شما می توانید این عبارت را جایگزین \(\sum_{i=1}^n i^2\) در آخرین خط از راه حل نماد سیگما کنید، و همزمان \(n\) را جایگزین \(\sum_{i=1}^n 1\) کنید:
$$R_n=\frac{27}{n^3} \sum_{i=1}^n i^2 + \frac{3}{n} \sum_{i=1}^n 1 \\
=\frac{27}{n^3} \cdot \frac{n(n+1)(2n+1)}{6} + \frac{3}{n} \cdot n \\
= \frac{27}{n^3} \cdot \frac{2n^3+3n^2+n}{6} + 3 \\
\frac{27}{n^3} \cdot \biggl( \frac{n^3}{3}+\frac{n^2}{2}+\frac{n}{6} \biggr) + 3 \\
=9+\frac{27}{2n} + \frac{9}{2n^2} + 3 \\
= 12 + \frac{27}{2n} + \frac{9}{2n^2}$$
بالاخره تمام شد! این فرمول مساحت \(n\) مستطیل راست بین \(x=0\) و \(x=3\)، زیر تابع \(f(x)=x^2+1\) می باشد. شما می توانید از این فرمول برای تولید مساحت تقریبی داده شده در جدول 2-14 استفاده کنید. اما هنگامی که به چنین فرمولی رسیدید، به نوعی بی معنا خواهد بود که جدولی از مساحت های تقریبی را تولید کنید، زیرا می توانید از این فرمول برای تعیین مساحت دقیق استفاده کنید. و این کار به سادگی یک بشکن زدن خواهد بود. در بخش بعدی به آن می پردازم.
اما قبل از آن، در اینجا فرمول های \(n\) مستطیل چپ و \(n\) مستطیل نقطۀ میانی بین \(x=0\) و \(x=3\) زیر همان تابع، \(x^2+1\) را می بینید. این فرمول ها تقریب های مساحت در جداول 1-14 و 3-14 را تولید می کنند. عملیات جبری مورد نیاز برای بدست آوردن این فرمولها حتی از چیزی که برای مستطیل راست انجام دادید، بدتر است، بنابراین من تصمیم گرفتم تا آنها را نادیده بگیرم. از نظر شما که اشکالی ندارد؟ من اینطور فکر نمی کنم.
$$L_n=12-\frac{27}{2n}+\frac{9}{2n^2} \\
M_n = 12 - \frac{9}{4n^2}$$

نماد جمع بندی یا نماد سیگما
برای جمع زدن سری های طولانی اعداد مانند مساحت مستطیل ها در یک جمع چپ، راست، یا نقطۀ میانی، نماد جمع بندی یا نماد سیگما (sigma notation) در دسترس است. در اینجا چگونگی کارکرد آن را می بینید. فرض کنید می خواهید \(100\) مضرب اول \(5\) را با یکدیگر جمع بزنید ـــ آن از \(5\) تا \(500\) است. شما می توانید این جمع را اینگونه بنویسید:
$$5+10+15+20+25+..........+490+495+500$$
اما با نماد سیگما (سیگما، \(\sum\)، هجدهمین حرف الفبای یونانی می باشد) این جمع بسیار متراکم تر و کارآمدتر است، و بیایید صادق باشیم، بسیار جالب به نظر می رسد:
$$\sum_{i=1}^{100} 5i$$
این نماد صرفاً به شما می گوید که \(1\) را در \(i\) در \(5i\) جایگذاری کنید، سپس \(2\) را در \(i\) در \(5i\) جایگذاری کنید، سپس \(3\)، سپس \(4\)، و به همین ترتیب، تا \(100\) ادامه بدهید. سپس نتایج را با یکدیگر جمع بزنید. بنابراین آن \(5 \cdot 1\) بعلاوۀ \(5 \cdot 2\) بعلاوۀ \(5 \cdot 3\)، و به همین ترتیب تا \(5 \cdot 100\) می باشد. این کار نتیجۀ یکسانی با نوشتن جمع به صورت طولانی دارد. در ضمن، حرف \(i\) هیچ معنای خاصی ندارد. شما می توانید این جمع را با یک \(j\)، یا هر حرف الفبای دیگری بنویسید:
$$\sum_{j=1}^{100} 5j$$
در این مثال دیگری داریم. اگر بخواهید جمع زیر را انجام دهید،
$$10^2 + 11^2 + 12^2 + .......... + 29^2 + 30^2$$
می توانید این جمع را با نماد سیگما به شکل زیر بنویسید:
$$\sum_{k=10}^{30} k^2$$
به همین سادگی.
نوشتن جمع های ریمان (Riemann sums) با نماد سیگما
شما می توانید از نماد سیگما برای نوشتن جمع مستطیل راست برای منحنی \(x^2+1\) که آن را مورد بررسی قرار دادیم، استفاده کنید.
فرمول جمع راست (right sum) را از بخش پیشین در همین فصل بخاطر آورید:
$$R_n=\frac{b-a}{n}[f(x_1)+f(x_2)+f(x_3)+..........+f(x_n)]$$
در اینجا همان فرمول را که با نماد سیگما نوشته شده است داریم:
$$R_n=\sum_{i=1}^n \biggl[f(x_i) \cdot \frac{b-a}{n} \biggr]$$
توجه داشته باشید که من می توانستم این فرمول را به شکل زیر نیز بنویسم که بیشتر و زیباتر انعکاس دهندۀ فرمول اصلی است، که در آن \(\frac{b-a}{n}\) در بیرون قرار گرفته است. هر دو روش خوب هستند ـــ آنها یکسانند ـــ اما انتخاب من این بوده است که \(\frac{b-a}{n}\) را در داخل قرار دهم، به نحوی که \(\sum\) در واقع جمع مستطیل ها باشد. به عبارت دیگر، با \(\frac{b-a}{n}\) در داخل، عبارت بعد از نماد \(\sum\)، یعنی \(f(x_i) \cdot \frac{b-a}{n}\)، که در آن نماد \(\sum\) به شما می گوید جمع بزنید، مساحت هر مستطیل می باشد، یعنی ارتفاع ضربدر قاعده.
$$R_n=\frac{b-a}{n} \sum_{i=1}^n f(x_i)$$
اکنون این را برای شش مستطیل راست در شکل 8-14 به کار بگیرید.

شما در حال محاسبۀ مساحت زیرِ منحنیِ \(x^2+1\) بین \(x=0\) و \(x=3\) با شش مستطیل هستید، بنابراین، عرض هر کدام برابر است با:
$$\frac{b-a}{n}=\frac{3-0}{6}=\frac{3}{6}=\frac{1}{2}$$
بنابراین خواهید داشت:
$$R_6=\sum_{i=1}^6 \biggl[f(x_i) \cdot \frac{1}{2} \biggr]$$
در ادامه، از آنجا که عرض هر مستطیل برابر با \(\frac{1}{2}\) است، لبه های راست این شش مستطیل در شش مضرب اول \(\frac{1}{2}\) قرار می گیرند: \(0.5, 1, 1.5, 2, 2.5, 3\) . این اعداد مختصات \(x\) های شش نقطۀ \(x_1\) تا \(x_6\) می باشند؛ آنها را می توانید با عبارت \(\frac{1}{2}i\) تولید کنید، که در آن \(i\) برابر با \(1\) تا \(6\) می باشد. شما می توانید با جایگذاری \(1\) برای \(i\) در \(\frac{1}{2}i\)، سپس \(2\)، سپس \(3\)، تا \(6\)، این امر را درست آزمایی کنید. اکنون می توانید \(x_i\) در این فرمول را با \(\frac{1}{2}i\) جایگذاری کنید که نتیجۀ زیر را به شما می دهد:
$$R_6=\sum_{i=1}^6 \biggl[ f \biggl( \frac{1}{2}i \biggr) \cdot \frac{1}{2} \biggr]$$
تابع ما، \(f(x)\)، برابر با \(x^2 + 1\) می باشد، بنابراین \(f(\frac{1}{2}i) = (\frac{1}{2}i)^2 + 1\)، و بنابراین می توانید بنویسید:
$$R_6=\sum_{i=1}^6 \biggl[ f \biggl( \bigl( \frac{1}{2}i \bigr)^2 + 1 \biggr) \cdot \frac{1}{2} \biggr]$$
اگر \(1\) را در \(i\) جایگذاری کنید، سپس \(2\) را، سپس \(3\)، و به همین ترتیب تا \(6\) ادامه دهید و عملیات ریاضی را انجام دهید، به جمع مساحت های مستطیل های موجود در شکل 8-14 می رسید. این نماد سیگما صرفاً یک روش فانتزی برای نوشتن جمع این شش مستطیل می باشد.
آیا مشغول تفریح هستیم؟ صبر کنید، بدتر هم می شود ـــ متاسفم. اکنون، شما می بایست شکل کلی این جمع را برای تعداد مجهول، \(n\)، مستطیل های راست، بنویسید. جمع محدودۀ مساحت در این سوال برابر با \(3\) می باشد، درست است؟ شما این محدوده را بر تعداد مستطیل ها تقسیم می کنید تا عرض هر مستطیل را بدست آورید. با \(6\) مستطیل، عرض هر کدام برابر با \(\frac{3}{6}\) می باشد؛ با \(n\) مستطیل، عرض هر کدام برابر با \(\frac{3}{n}\) می باشد. و لبۀ راست این \(n\) مستطیل با \(\frac{3}{n}i\)، برای \(i\) برابر است با \(1\) تا \(n\)، تولید می شود. این به شما نتیجۀ زیر را می دهد:
$$R_n=\sum_{i=1}^n \biggl[ f \biggl( \frac{3}{n}i \biggr) \cdot \frac{3}{n} \biggr]$$
از آنجا که \(f(x)=x^2 + 1\)، خواهیم داشت:
$$
R_n=\sum_{i=1}^n \biggl[ \biggl( \bigl( \frac{3}{n}i \bigr)^2 + 1 \biggr) \cdot \frac{3}{n} \biggr] \\
=\sum_{i=1}^n \biggl[ \biggl( \frac{9i^2}{n^2} + 1 \biggr) \cdot \frac{3}{n} \biggr] \\
=\sum_{i=1}^n \biggl[ \frac{27i^2}{n^3} + \frac{3}{n} \biggr]
$$
در مورد دو خط بعدی این عملیات فعلاً به من اعتماد کنید تا در آینده برایتان روشن شود:
$$
=\sum_{i=1}^n \frac{27i^2}{n^3} + \sum_{i=1}^n \frac{3}{n} \\
=\frac{27}{n^3} \sum_{i=1}^n i^2 + \frac{3}{n} \sum_{i=1}^n 1
$$
در آخرین مرحله، شما می توانید \(\frac{27}{n^3}\) و \(\frac{3}{n}\) را از درون نماد جمع بیرون بکشید ـــ شما اجازه دارید هر چیزی به جز تابعی از \(i\)، که به آن ایندکس جمع گفته می شود، را از آنجا بیرون بکشید. همچنین جمع دوم در مرحلۀ آخر تنها یک \(1\) بعد از آن دارد و \(i\) ندارد. بنابراین جایی برای جایگذاری مقدار \(i\) وجود ندارد. این وضعیت ممکن است اندکی عجیب به نظر آید، اما تمام کاری که شما باید انجام دهید اینست که \(n\) بار \(1\) ها را با یکدیگر جمع بزنید، که برابر با \(n\) می شود (من این کار را در زیر انجام داده ام).
شما اکنون به یک مرحلۀ حیاتی رسیده اید. با یک تردستی، شما جمع ریمان بالا را به فرمولی به لحاظ \(n\) تبدیل خواهید کرد. این فرمول چیزی است که در بخش بعدی استفاده می کنید تا مساحت دقیق زیر این منحنی را بدست آورید.
اکنون، همانطور که تقریباً هیچ کس نمی داند، جمع \(n\) مربع اول، \(1^2+2^2+3^2+..........+n^2\)، برابر است با \(\frac{n(n+1)(2n+1)}{6}\) . (راستی، این عدد \(6\) هیچ ارتباطی به این واقعیت که ما از \(6\) مستطیل در چند صفحۀ قبل استفاده کردیم ندارد.) بنابراین شما می توانید این عبارت را جایگزین \(\sum_{i=1}^n i^2\) در آخرین خط از راه حل نماد سیگما کنید، و همزمان \(n\) را جایگزین \(\sum_{i=1}^n 1\) کنید:
$$R_n=\frac{27}{n^3} \sum_{i=1}^n i^2 + \frac{3}{n} \sum_{i=1}^n 1 \\
=\frac{27}{n^3} \cdot \frac{n(n+1)(2n+1)}{6} + \frac{3}{n} \cdot n \\
= \frac{27}{n^3} \cdot \frac{2n^3+3n^2+n}{6} + 3 \\
\frac{27}{n^3} \cdot \biggl( \frac{n^3}{3}+\frac{n^2}{2}+\frac{n}{6} \biggr) + 3 \\
=9+\frac{27}{2n} + \frac{9}{2n^2} + 3 \\
= 12 + \frac{27}{2n} + \frac{9}{2n^2}$$
بالاخره تمام شد! این فرمول مساحت \(n\) مستطیل راست بین \(x=0\) و \(x=3\)، زیر تابع \(f(x)=x^2+1\) می باشد. شما می توانید از این فرمول برای تولید مساحت تقریبی داده شده در جدول 2-14 استفاده کنید. اما هنگامی که به چنین فرمولی رسیدید، به نوعی بی معنا خواهد بود که جدولی از مساحت های تقریبی را تولید کنید، زیرا می توانید از این فرمول برای تعیین مساحت دقیق استفاده کنید. و این کار به سادگی یک بشکن زدن خواهد بود. در بخش بعدی به آن می پردازم.
اما قبل از آن، در اینجا فرمول های \(n\) مستطیل چپ و \(n\) مستطیل نقطۀ میانی بین \(x=0\) و \(x=3\) زیر همان تابع، \(x^2+1\) را می بینید. این فرمول ها تقریب های مساحت در جداول 1-14 و 3-14 را تولید می کنند. عملیات جبری مورد نیاز برای بدست آوردن این فرمولها حتی از چیزی که برای مستطیل راست انجام دادید، بدتر است، بنابراین من تصمیم گرفتم تا آنها را نادیده بگیرم. از نظر شما که اشکالی ندارد؟ من اینطور فکر نمی کنم.
$$L_n=12-\frac{27}{2n}+\frac{9}{2n^2} \\
M_n = 12 - \frac{9}{4n^2}$$
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: