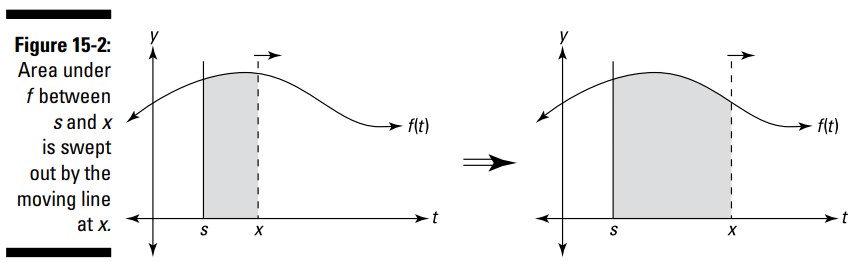
این مورد سخت است ـــ خودتان را برای مواجهه با آن آماده کنید. فرض کنید هر تابع قدیمی، \(f(t)\)، را دارید، تصور کنید که در مقدار \(t\) خاصی، آن را \(s\) بنامید، شما یک خط ثابت عمودی ترسیم می کنید. شکل 2-15 را ببینید.





سپس یک خط عمودی قابل حرکت دادن را در نظر بگیرید، که در همان نقطۀ \(s\) آغاز می شود، و آن را به سمت راست بکشید. همینطور که این خط را می کشید، مساحت بزرگتر و بزرگتری را در زیر این منحنی ایجاد می کنید. این مساحت تابعی از \(x\)، موقعیت خط در حال حرکت، می باشد. با نمادها آن را اینگونه می نویسید:
$$A_f(x)= \int_s^x f(x) dt$$

توجه داشته باشید که \(t\) متغیر ورودی در \(f(t)\) می باشد، در واقع \(t\) جایگزین \(x\) شده است زیرا \(x\) در حال حاضر به چیز دیگری تخصیص داده شده است ـــ آن متغیر ورودی در \(A_f(x)\) می باشد. زیرنویسِ \(f\) در \(A_f\) نشان دهندۀ اینست که \(A_f(x)\) تابع مساحت برای منحنی خاص \(f\) یا \(f(t)\) می باشد. \(dt\) یک افزایش کوچک ـــ در واقع یک افزایش بی نهایت کوچک ـــ در امتداد محور \(t\) می باشد.

در اینجا مثال ساده ای داریم تا اطمینان حاصل کنیم که شما درک کرده اید یک تابع مساحت چگونه کار می کند. در ضمن، اگر درک این برایتان بسیار مشکل باشد، احساس بدی پیدا نکنید ـــ شما همراهان زیادی دارید. فرض کنید این تابع ساده را داشته باشید، \(f(t)=10\)، این یک خط افقی در \(y=10\) می باشد. اگر این مساحت را که در \(s=3\) آغاز می شود بکشید، به تابع مساحت زیر می رسید:
$$A_f(x)=\int_3^x 10 dt$$
شما می توانید ببینید که مساحت کشیده شده از \(3\) تا \(4\) برابر با \(10\) می باشد، زیرا در کشیدن این خط از \(3\) به \(4\)، شما یک مستطیل با عرض \(1\) و ارتفاع \(10\) بیرون می کشید، که دارای مساحت \(1\) ضربدر \(10\)، یا \(10\) می باشد. شکل 3-15 را ببینید.


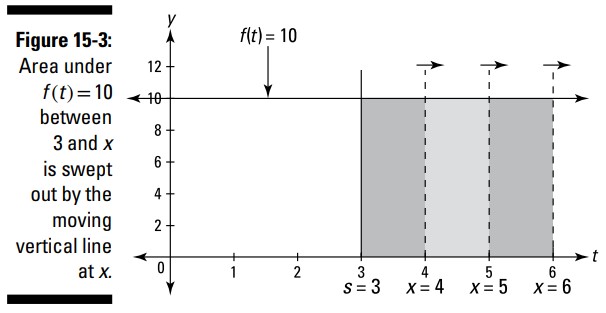
بنابراین، \(A_f(4)\)، مساحت بیرون کشیده شده همچنانکه شما به \(4\)می رسید، برابر با \(10\) می باشد. \(A_f(5)\) برابر با \(20\) می باشد زیرا هنگامی که این خط را به \(5\) بکشید، مستطیلی با عرض \(2\) و ارتفاع \(10\) را بیرون می کشید، که مساحت آن برابر با \(2 \times 10 = 20\) می باشد. \(A_f(6)\) برابر با \(30\) می باشد، و به همین ترتیب ادامه می یابد.

اکنون فرض کنید این خط را در امتداد یک نرخ یک واحد بر ثانیه می کشید. شما در \(x=3\) آغاز می کنید، و به \(4\) در \(1\) ثانیه می رسید، \(5\) در \(2\) ثانیه، \(6\) در \(3\) ثانیه، و به همین ترتیب. چه مساحتی را در هر ثانیه می گسترانید؟ ده واحد مربع بر ثانیه، زیرا در هر ثانیه شما \(1\) بر \(10\) مستطیل دیگر را می گسترانید. توجه داشته باشید ـــ این مهم است ـــ از آنجا که عرض هر مستطیلی که گسترشش می دهید برابر با \(1\) می باشد، مساحت هر مستطیل ـــ که با طول ضربدر عرض بدست می آید ـــ برابر با ارتفاع آن می باشد، زیرا هر چیزی ضربدر \(1\) برابر با خودش می شود. شما بزودی خواهید فهمید چرا این نکتۀ مهمی است. در ضمن، نرخ اصلی که ما در موردش اهمیت می دهیم مساحت گسترش داده شده در هر ثانیه نمی باشد، اما، نسبتاً، مساحت گسترانده شده در هر تغییر واحد بر روی محور \(x\) می باشد. من به این دلیل آن را با واژۀ بر ثانیه توضیح دادم که فکر کردن در مورد گسترش مساحت با این نرخ ساده تر است. و از آنجاییکه شما این خط را در امتداد محور \(x\) یک واحد در هر ثانیه می کشید، هر دو نرخ یکسان می باشند. شما می توانید انتخاب خودتان را داشته باشید.


دوباره، این صرفاً به شما می گوید که با هر افزایش \(1\) واحدی در \(x\)، \(A_f\) (تابع مساحت) \(10\) واحد بالا می آید. اکنون چیز حیاتی اینجاست: توجه داشته باشید که این نرخ یا مشتق \(10\) برابر با ارتفاع تابع اصلی \(f(t)=10\) می باشد زیرا همینطور که \(1\) واحد رو به جلو پیش می روید، مستطیلی را گسترش می دهید که \(1\) در \(10\) می باشد، که دارای مساحت \(10\) است، یعنی ارتفاع آن تابع.

و این نرخ صرفنظر از عرض این مستطیل با \(10\) حل می شود. فرض کنید که این خط عمودی را از \(x=4\) به \(x=4.001\) کشیده اید. در نرخ یک واحد بر ثانیه، این به شما \(\frac{1}{1000}\)ام یک ثانیه را می دهد، و شما یک مستطیل لاغرمردنی با عرض \(\frac{1}{1000}\) یا \(\frac{1}{100}\) واحد مربع، را گسترش می دهید. بنابراین نرخ مساحتی که گسترانده می شود برابر با \(\frac{\frac{1}{100} \text{ square units}}{\frac{1}{1000} \text{ square units}}\) می باشد که برابر با \(10\) واحد مربع (square units) در ثانیه است. بنابراین می بینید که با هر افزایش کوچک در امتداد محور \(x\)، نرخ این مساحت برابر با ارتفاع تابع گسترش می یابد.

این برای هر تابعی، و نه فقط برای خطهای افقی، درست جواب می دهد. به تابع \(g(t)\) و تابع مساحت آن \(A_g(x)\) بنگرید که گسترش مساحت آن از \(s=2\) در شکل 4-15 آغاز می گردد.


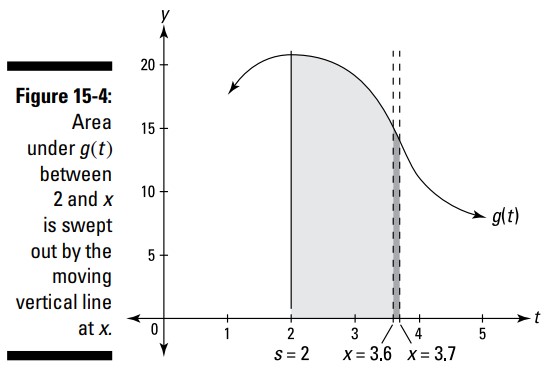
بین \(x=3.6\) و \(x=3.7\)، \(A_g(x)\) با مساحت آن مستطیل تیرۀ لاغر مردنی با عرض \(0.1\) و ارتفاعی در حدود \(15\) رشد می کند. همانطور که می توانید ببینید آن واقعاً یک مستطیل نیست؛ بیشتر به یک ذوزنقه نزدیک است، اما آن هم نیست زیرا بالای کوچک آن اندکی منحنی است. اما، در حد، همینطور که عرض ها کوچکتر و کوچکتر می شوند، آن مستطیل لاغرمردنی دقیقاً مانند یک مستطیل واقعی عمل می کند. بنابراین، دوباره می گویم، \(A_g(x)\) با مساحت آن مستطیل تیره رشد می کند که دارای مساحتی به شدت نزدیک به \(0.1\) ضربدر \(15\) می باشد. این مساحت با \(0.1\) ثانیه گسترانده می شود، بنابراین نرخ مساحت گسترانده شده برابر با \(\frac{1.5 \text{ square units}}{0.1 \text{ seconds}}\) یا \(15\) واحد مربع بر ثانیه (square units per second) ، ارتفاع این تابع، می باشد.