خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
قضیۀ اساسی حسابان

شیپورها را به صدا در بیاورید! حالا که ارتباط بین نرخ رشدِ یک تابع مساحت و ارتفاع منحنی داده شده را دیدید، شما برای قضیۀ اساسی حسابان (fundamental theorem of calculus) آماده هستید ـــ چیزی که به گفتۀ برخی ها یکی از مهمترین قضایای تاریخ ریاضیات می باشد.

اکنون، از آنجا که مشتق \(A_f(x)\) برابر با \(f(x)\) می باشد، بنا به تعریف \(A_f(x)\) یک ضدمشتق از \(f(x)\) می باشد. با بازگشت به تابع ساده از بخش قبلی، \(f(t)=10\)، و تابع مساحت آن، \(A_f(x)=\int_s^x 10dt\)، چگونگی کارکرد این را بررسی کنید.
بنا بر قضیۀ اساسی حسابان، \(\frac{d}{dx} A_f(x)=10\) . بنابراین \(A_f\) باید ضدمشتقی از \(10\) باشد؛ به عبارت دیگر، \(A_f\) تابعی است که مشتق آن برابر با \(10\) می باشد. از آنجا که هر تابعی در شکل \(10x+C\)، که در آن \(C\) یک عدد می باشد، دارای مشتقی از \(10\) می باشد، ضدمشتق \(10\) برابر با \(10x+C\) می باشد. عدد خاص \(C\) بستگی به انتخاب شما از \(s\)، نقطه ای که گسترش مساحت را از آنجا آغاز می کنید، دارد. برای یک انتخاب خاص از \(s\)، تابع مساحت تابعی خواهد بود (خارج از تمامی توابع موجود در خانوادۀ منحنی های \(10x+C\)) که محور \(x\) را در \(s\) قطع می کند. برای بدست آوردن \(C\)، ضدمشتق را برابر با صفر قرار دهید، مقادیر \(s\) را در \(x\) جایگذاری کنید، و آن را برای بدست آوردن \(C\) حل کنید.
برای این تابع با یک ضدمشتق از \(10x+C\) ، اگر شما گسترش مساحت را ، فرضاً در \(s=0\)، آغاز کنید، سپس \(10 \cdot 0+C=0\)، بنابراین \(C=0\)، و بدین ترتیب، \(A_f(x)=\int_0^x 10dt=10x+C\)، یا فقط \(10x\). (توجه داشته باشید که \(C\) الزاماً برابر با \(s\) نمی باشد. در واقع، آن معمولاً اینطور نیست (مخصوصاً وقتی که \(s \ne 0\)) . وقتیکه \(s=0\)، \(C\) نیز اغلب برابر با \(0\) است، اما نه برای تمامی توابع.)
شکل 5-15 نشان می دهد اگر گسترش مساحت را در صفر آغاز کنید، چرا \(A_f(x)=10x\) تابع مساحت صحیح می باشد. در نمودار بالایی در شکل، مساحت زیر منحنی از \(0\) تا \(3\) برابر با \(30\) می باشد، و آن با \(A_f(3)=10 \cdot 3=30\) بدست می آید. و می توانید ببینید که مساحت از \(0\) تا \(5\) برابر با \(50\) می باشد، که با واقعیت \(A_f(5)=10 \cdot 5 = 50\) همخوانی دارد.
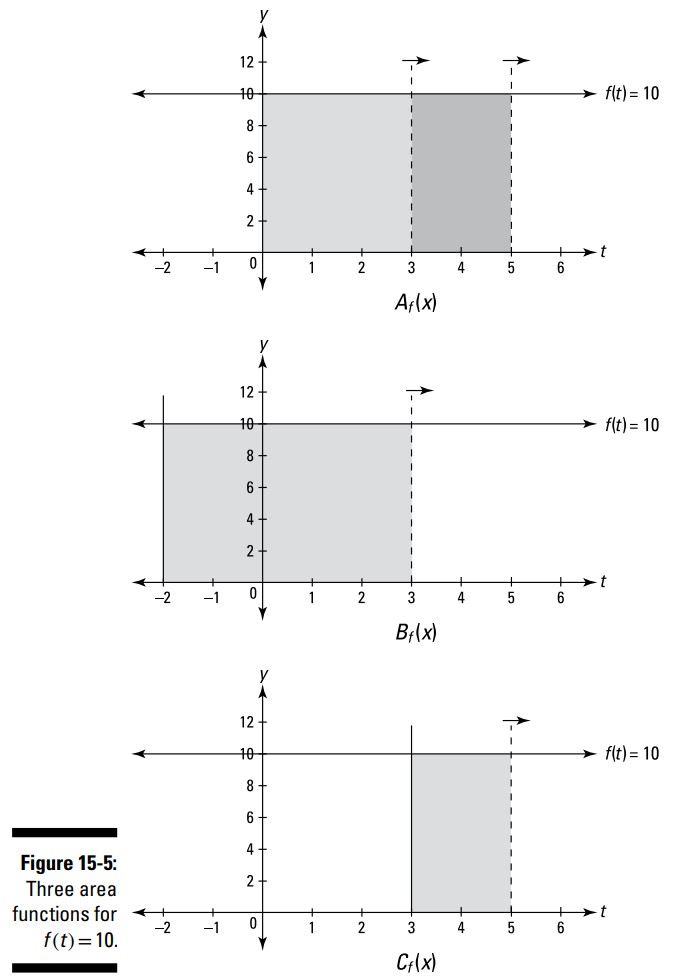
اگر در عوض، شما گسترش مساحت را در \(s=-2\) آغاز کنید و یک تابع مساحت جدید تعریف کنید، \(B_f(x)=\int_{-2}^x 10dt\)، سپس \(10 \cdot (-2) + C = 0\)، بنابراین \(C\) برابر با \(20\) و بدین ترتیب \(B_f(x)\) برابر با \(10x+20\) خواهد بود.
این تابع مساحت \(20\) تا بیشتر از \(A_f(x)\) است، که در \(s=0\) آغاز می شود، زیرا اگر شما در \(s=-2\) آغاز کنید، مساحتی برابر با \(20\) ضربدر ....
این تابع مساحت برابر با \(20\) بیشتر از \(A_f(x)\)، که در \(s=0\) آغاز می شود، است، زیرا اگر شما در \(s=-2\) آغاز کنید، شما هم اکنون مساحتی معادل \(20\) را نسبت به زمانی که از صفر آغاز می کنید، گسترش داده اید. شکل 5-15 به شما نشان می دهد چرا \(B_f(3)\) برابر با \(20\) بیشتر از \(A_f(x)\) است.
اگر گسترش مساحت را در \(s=3\) آغاز کنید، \(10 \cdot 3 + C=0\)، بنابراین \(C=-30\) و این تابع مساحت برابر با \(C_f(x)=\int_3^x 10dt=10x-30\). این تابع \(30\) کمتر از \(A_f(x)\) است، زیرا در \(C_f(x)\)، شما به اندازۀ \(3\) در \(10\) مستطیل بین \(0\) و \(3\) که در \(A_f(x)\) وجود دارد، از دست می دهید (نمودار پایینی در شکل 5-15 را ببینید).
حالا بیایید به نمودارهای \(A_f(x)\)، \(B_f(x)\)، و \(C_f(x)\) نگاهی بیندازیم. (توجه داشته باشید که شکل \(5-15\) نمودارهای \(A_f(x)\)، \(B_f(x)\)، و \(C_f(x)\) را نشان نمی دهد. شما سه نمودار از تابع خط افقی، \(f(t)=10\) می بینید؛ و مساحت گسترانده شده زیر \(f(t)\) توسط \(A_f(x)\)، \(B_f(x)\)، و \(C_f(x)\) را می بینید، اما در واقع نمودارهای این سه تابع را نمی بینید.) شکل 6-15 را بررسی کنید.
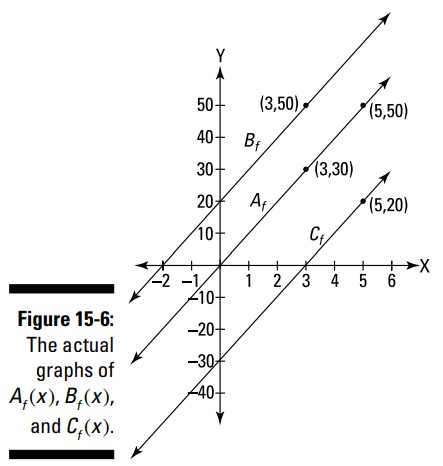
شکل 6-15 نمودار معادلات \(A_f(x)\)، \(B_f(x)\)، و \(C_f(x)\) را که پیشتر آنها را حل کردیم به شما نشان می دهد: \(A_f(x)=10x\)، \(B_f(x)=10x+20\)، و \(C_f(x)=10x-30\). (همانطور که می بینید هر سۀ اینها به سادگی خطهایی با شکل \(y=mx+b\) می باشند.) مقادیر \(y\) در این سه تابع، مساحت های گسترانده شده زیر \(f(t)=10\) که در شکل 5-15 دیدید را به شما می دهند. توجه داشته باشید که سه طول از مبدأ (x-intercepts) که در شکل 6-15 می بینید سه مقدار \(x\) در شکل 5-15 می باشند که گسترش مساحت از آنجا آغاز می شود.
ما قبلاً حل کرده بودیم که \(A_f(3)=30\) و \(A_f(5)=50\). شما می توانید این دو مساحت \(30\) و \(50\) را در نمودار بالا در شکل 5-15 ببینید. در شکل 6-15 شما این نتایج را روی \(A_f\) در نقاط \((3,30)\) و \((5,50)\) می بینید. شما همچنین در شکل 5-15 دیدید که \(B_f(3)\) برابر با \(20\) بیشتر از \(A_f(3)\) بود؛ در شکل 6-15 این نتیجه را در \((3,50)\) بر روی \(B_f\) می بینید که \(20\) بالاتر از \((3,30)\) روی \(A_f\) است. در نهایت در شکل 5-15 دیدید که \(C_f(x)\) برابر با \(30\) کمتر از \(A_f(x)\) است. شکل 6-15 آن را به روش متفاوتی نشان می دهد: در هر مقدار \(x\)، خط \(C_f\) برابر با \(30\) واحد زیر خط \(A_f\) می باشد.
چند ملاحظات. شما هم اکنون از روی قضیۀ اصلی حسابان می دانید که \(\frac{d}{dx}A_f(x)=f(x)=10\) (و چیز یکسانی در مورد \(B_f(x)\) و \(C_f(x)\) داریم). که بالاتر به لحاظ نرخ ها توضیح داده شدند: برای \(A_f\)، \(B_f\)، و \(C_f\)، نرخ مساحت گسترانده شده زیر \(f(t)=10\) برابر با \(10\) می باشد. همچنین شکل 6-15 نشان می دهد که \(\frac{d}{dx}A_f(x)=10\) (و چیز یکسانی در مورد \(B_f\) و \(C_f\) داریم)، اما در اینجا شما این مشتق را به شکل شیب می بینید. مطمئناً شیب هر سۀ این خطها برابر با \(10\) می باشند. در نهایت، توجه کنید که ـــ مانند چیزی که در شکل 1-15 دیدید ـــ سه خط موجود در شکل 6-15، صرفاً با یک انتقال عمودی (vertical translation) با یکدیگر فرق می کنند. این سه خط (و تمامی بی نهایت خطهای دیگری که به صورت عمودی منتقل شده اند) همگی عضوی از کلاس توابع \(10x+C\)، یعنی خانوادۀ ضدمشتق های \(f(x)=10\)، می باشند.
برای مثال بعدی، دوباره به سهمی \(y=x^2+1\)، دوست ما از فصل 14 که آن را به لحاظ جمع مساحت های مستطیل ها (جمع ریمان) بررسی کردیم، بیندازید. به شکل 4-14 بازگردید، و ناحیۀ سایه دار شده زیر \(y=x^2+1\) را بررسی کنید. اکنون می توانید مساحت دقیق این ناحیه سایه دار شده را با روشی آسان، محاسبه کنید.
تابع مساحت زیر \(x^2+1\) برابر با \(A_f(x)=\int_s^x (t^2 + 1)dt\) می باشد. بنابر قضیۀ اساسی حسابان، \(\frac{d}{dx} A_f(x)=x^2 + 1\)، و بنابراین \(A_f\) ضدمشتقی از \(x^2+1\) می باشد. هر تابعی در شکل \(\frac{1}{3}x^3 + x + C\) دارای مشتقی از \(x^2+1\) می باشد (خودتان می توانید امتحان کنید)، بنابراین آن ضدمشتق است. در شکل 6-14 ، شما می خواهید مساحتی را گسترش دهید که از \(0\) آغاز می شود، بنابراین \(s=0\). ضدمشتق را برابر با صفر قرار دهید، مقدار \(s\) را در \(x\) جایگذاری کنید، و آن را برای بدست آوردن \(C\) حل کنید: \(\frac{1}{3} \cdot 0^3 + 0 + C = 0\)، بنابراین \(C=0\)، و بدین ترتیب:
$$A_f(x)=\int_0^x (t^2 + 1 )dt=\frac{1}{3}x^3 + x + 0$$
مساحت گسترانیده شده از \(0\) تا \(3\) ـــ که ما آن را در فصل 14 به روش سخت محاسبۀ حد جمع ریمان انجام دادیم ـــ به سادگی \(A_f(3)\) است:
$$A_f(x)=\frac{1}{3}x^3 + x \\
A_f(3)=\frac{1}{3} \cdot 3^3 + 3 = 9 + 3 = 12 $$
به همین سادگی. این کار بسیار کمتری نسبت به انجام آن با روش سخت داشت.
و بعد از اینکه دانستید این تابع مساحت که در صفر آغاز می شود، \(\int_0^x (t^2+1)dt\)، برابر با \(\frac{1}{3}x^3 + x\) است، یافتن سایر مساحتهای زیر این سهمی که از صفر آغاز نمی شوند به سادگی یک بشکن زدن است. به عنوان مثال، فرض کنید، می خواهید مساحت زیر این سهمی را بین \(2\) و \(3\) بدست آورید. شما می توانید این مساحت را با تفریق مساحت بین \(0\) و \(2\) از مساحت بین \(0\) و \(3\) محاسبه کنید. شما اندکی پیش مساحت بین \(0\) و \(3\) را بدست آورده اید ـــ که \(12\) می باشد. و مساحت بین \(0\) و \(2\) برابر با \(A_f(2)=\frac{1}{3} \cdot 2^3 + 2 = 4\frac{2}{3}\) می باشد. بنابراین مساحت بین \(2\) و \(3\) برابر با \(12- 4 \frac{2}{3} = 7\frac{1}{3}\) می باشد.

قضیۀ اساسی حسابان (fundamental theorem of calculus): در تابع معین \(A_f\) که مساحت زیر \(f(t)\) را می گستراند،
$$A_f(x)=\int_s^x f(t)dt$$
نرخی که در آن مساحت گسترانده می شود با ارتفاع تابع اصلی برابر است. بنابراین، از آنجا که این نرخ مشتق می باشد، مشتق این تابع مساحت برابر با تابع اصلی می باشد:
$$\frac{d}{dx}A_f(x)=f(x)$$
از آنجا که \(A_f(x)=\int_s^x f(t)dt\)، شما همچنین می توانید معادلۀ بالا را به شکل زیر بنویسید:
$$\frac{d}{dx} \int_s^x f(t)dt=f(x)$$
$$A_f(x)=\int_s^x f(t)dt$$
نرخی که در آن مساحت گسترانده می شود با ارتفاع تابع اصلی برابر است. بنابراین، از آنجا که این نرخ مشتق می باشد، مشتق این تابع مساحت برابر با تابع اصلی می باشد:
$$\frac{d}{dx}A_f(x)=f(x)$$
از آنجا که \(A_f(x)=\int_s^x f(t)dt\)، شما همچنین می توانید معادلۀ بالا را به شکل زیر بنویسید:
$$\frac{d}{dx} \int_s^x f(t)dt=f(x)$$
اکنون، از آنجا که مشتق \(A_f(x)\) برابر با \(f(x)\) می باشد، بنا به تعریف \(A_f(x)\) یک ضدمشتق از \(f(x)\) می باشد. با بازگشت به تابع ساده از بخش قبلی، \(f(t)=10\)، و تابع مساحت آن، \(A_f(x)=\int_s^x 10dt\)، چگونگی کارکرد این را بررسی کنید.
بنا بر قضیۀ اساسی حسابان، \(\frac{d}{dx} A_f(x)=10\) . بنابراین \(A_f\) باید ضدمشتقی از \(10\) باشد؛ به عبارت دیگر، \(A_f\) تابعی است که مشتق آن برابر با \(10\) می باشد. از آنجا که هر تابعی در شکل \(10x+C\)، که در آن \(C\) یک عدد می باشد، دارای مشتقی از \(10\) می باشد، ضدمشتق \(10\) برابر با \(10x+C\) می باشد. عدد خاص \(C\) بستگی به انتخاب شما از \(s\)، نقطه ای که گسترش مساحت را از آنجا آغاز می کنید، دارد. برای یک انتخاب خاص از \(s\)، تابع مساحت تابعی خواهد بود (خارج از تمامی توابع موجود در خانوادۀ منحنی های \(10x+C\)) که محور \(x\) را در \(s\) قطع می کند. برای بدست آوردن \(C\)، ضدمشتق را برابر با صفر قرار دهید، مقادیر \(s\) را در \(x\) جایگذاری کنید، و آن را برای بدست آوردن \(C\) حل کنید.
برای این تابع با یک ضدمشتق از \(10x+C\) ، اگر شما گسترش مساحت را ، فرضاً در \(s=0\)، آغاز کنید، سپس \(10 \cdot 0+C=0\)، بنابراین \(C=0\)، و بدین ترتیب، \(A_f(x)=\int_0^x 10dt=10x+C\)، یا فقط \(10x\). (توجه داشته باشید که \(C\) الزاماً برابر با \(s\) نمی باشد. در واقع، آن معمولاً اینطور نیست (مخصوصاً وقتی که \(s \ne 0\)) . وقتیکه \(s=0\)، \(C\) نیز اغلب برابر با \(0\) است، اما نه برای تمامی توابع.)
شکل 5-15 نشان می دهد اگر گسترش مساحت را در صفر آغاز کنید، چرا \(A_f(x)=10x\) تابع مساحت صحیح می باشد. در نمودار بالایی در شکل، مساحت زیر منحنی از \(0\) تا \(3\) برابر با \(30\) می باشد، و آن با \(A_f(3)=10 \cdot 3=30\) بدست می آید. و می توانید ببینید که مساحت از \(0\) تا \(5\) برابر با \(50\) می باشد، که با واقعیت \(A_f(5)=10 \cdot 5 = 50\) همخوانی دارد.

اگر در عوض، شما گسترش مساحت را در \(s=-2\) آغاز کنید و یک تابع مساحت جدید تعریف کنید، \(B_f(x)=\int_{-2}^x 10dt\)، سپس \(10 \cdot (-2) + C = 0\)، بنابراین \(C\) برابر با \(20\) و بدین ترتیب \(B_f(x)\) برابر با \(10x+20\) خواهد بود.
این تابع مساحت \(20\) تا بیشتر از \(A_f(x)\) است، که در \(s=0\) آغاز می شود، زیرا اگر شما در \(s=-2\) آغاز کنید، مساحتی برابر با \(20\) ضربدر ....
این تابع مساحت برابر با \(20\) بیشتر از \(A_f(x)\)، که در \(s=0\) آغاز می شود، است، زیرا اگر شما در \(s=-2\) آغاز کنید، شما هم اکنون مساحتی معادل \(20\) را نسبت به زمانی که از صفر آغاز می کنید، گسترش داده اید. شکل 5-15 به شما نشان می دهد چرا \(B_f(3)\) برابر با \(20\) بیشتر از \(A_f(x)\) است.
اگر گسترش مساحت را در \(s=3\) آغاز کنید، \(10 \cdot 3 + C=0\)، بنابراین \(C=-30\) و این تابع مساحت برابر با \(C_f(x)=\int_3^x 10dt=10x-30\). این تابع \(30\) کمتر از \(A_f(x)\) است، زیرا در \(C_f(x)\)، شما به اندازۀ \(3\) در \(10\) مستطیل بین \(0\) و \(3\) که در \(A_f(x)\) وجود دارد، از دست می دهید (نمودار پایینی در شکل 5-15 را ببینید).
تابع مساحت یک ضد مشتق می باشد. مساحت گسترانده شده زیر خط افقی \(f(t)=10\)، از عدد خاص \(s\) تا \(x\)، با ضدمشتقی از \(10\) بدست می آید، یعنی \(10x+C\)، که در آن مقدار \(C\) بستگی به این دارد که گسترش مساحت را از چه نقطه ای آغاز می کنید.
حالا بیایید به نمودارهای \(A_f(x)\)، \(B_f(x)\)، و \(C_f(x)\) نگاهی بیندازیم. (توجه داشته باشید که شکل \(5-15\) نمودارهای \(A_f(x)\)، \(B_f(x)\)، و \(C_f(x)\) را نشان نمی دهد. شما سه نمودار از تابع خط افقی، \(f(t)=10\) می بینید؛ و مساحت گسترانده شده زیر \(f(t)\) توسط \(A_f(x)\)، \(B_f(x)\)، و \(C_f(x)\) را می بینید، اما در واقع نمودارهای این سه تابع را نمی بینید.) شکل 6-15 را بررسی کنید.

شکل 6-15 نمودار معادلات \(A_f(x)\)، \(B_f(x)\)، و \(C_f(x)\) را که پیشتر آنها را حل کردیم به شما نشان می دهد: \(A_f(x)=10x\)، \(B_f(x)=10x+20\)، و \(C_f(x)=10x-30\). (همانطور که می بینید هر سۀ اینها به سادگی خطهایی با شکل \(y=mx+b\) می باشند.) مقادیر \(y\) در این سه تابع، مساحت های گسترانده شده زیر \(f(t)=10\) که در شکل 5-15 دیدید را به شما می دهند. توجه داشته باشید که سه طول از مبدأ (x-intercepts) که در شکل 6-15 می بینید سه مقدار \(x\) در شکل 5-15 می باشند که گسترش مساحت از آنجا آغاز می شود.
ما قبلاً حل کرده بودیم که \(A_f(3)=30\) و \(A_f(5)=50\). شما می توانید این دو مساحت \(30\) و \(50\) را در نمودار بالا در شکل 5-15 ببینید. در شکل 6-15 شما این نتایج را روی \(A_f\) در نقاط \((3,30)\) و \((5,50)\) می بینید. شما همچنین در شکل 5-15 دیدید که \(B_f(3)\) برابر با \(20\) بیشتر از \(A_f(3)\) بود؛ در شکل 6-15 این نتیجه را در \((3,50)\) بر روی \(B_f\) می بینید که \(20\) بالاتر از \((3,30)\) روی \(A_f\) است. در نهایت در شکل 5-15 دیدید که \(C_f(x)\) برابر با \(30\) کمتر از \(A_f(x)\) است. شکل 6-15 آن را به روش متفاوتی نشان می دهد: در هر مقدار \(x\)، خط \(C_f\) برابر با \(30\) واحد زیر خط \(A_f\) می باشد.
چند ملاحظات. شما هم اکنون از روی قضیۀ اصلی حسابان می دانید که \(\frac{d}{dx}A_f(x)=f(x)=10\) (و چیز یکسانی در مورد \(B_f(x)\) و \(C_f(x)\) داریم). که بالاتر به لحاظ نرخ ها توضیح داده شدند: برای \(A_f\)، \(B_f\)، و \(C_f\)، نرخ مساحت گسترانده شده زیر \(f(t)=10\) برابر با \(10\) می باشد. همچنین شکل 6-15 نشان می دهد که \(\frac{d}{dx}A_f(x)=10\) (و چیز یکسانی در مورد \(B_f\) و \(C_f\) داریم)، اما در اینجا شما این مشتق را به شکل شیب می بینید. مطمئناً شیب هر سۀ این خطها برابر با \(10\) می باشند. در نهایت، توجه کنید که ـــ مانند چیزی که در شکل 1-15 دیدید ـــ سه خط موجود در شکل 6-15، صرفاً با یک انتقال عمودی (vertical translation) با یکدیگر فرق می کنند. این سه خط (و تمامی بی نهایت خطهای دیگری که به صورت عمودی منتقل شده اند) همگی عضوی از کلاس توابع \(10x+C\)، یعنی خانوادۀ ضدمشتق های \(f(x)=10\)، می باشند.
برای مثال بعدی، دوباره به سهمی \(y=x^2+1\)، دوست ما از فصل 14 که آن را به لحاظ جمع مساحت های مستطیل ها (جمع ریمان) بررسی کردیم، بیندازید. به شکل 4-14 بازگردید، و ناحیۀ سایه دار شده زیر \(y=x^2+1\) را بررسی کنید. اکنون می توانید مساحت دقیق این ناحیه سایه دار شده را با روشی آسان، محاسبه کنید.
تابع مساحت زیر \(x^2+1\) برابر با \(A_f(x)=\int_s^x (t^2 + 1)dt\) می باشد. بنابر قضیۀ اساسی حسابان، \(\frac{d}{dx} A_f(x)=x^2 + 1\)، و بنابراین \(A_f\) ضدمشتقی از \(x^2+1\) می باشد. هر تابعی در شکل \(\frac{1}{3}x^3 + x + C\) دارای مشتقی از \(x^2+1\) می باشد (خودتان می توانید امتحان کنید)، بنابراین آن ضدمشتق است. در شکل 6-14 ، شما می خواهید مساحتی را گسترش دهید که از \(0\) آغاز می شود، بنابراین \(s=0\). ضدمشتق را برابر با صفر قرار دهید، مقدار \(s\) را در \(x\) جایگذاری کنید، و آن را برای بدست آوردن \(C\) حل کنید: \(\frac{1}{3} \cdot 0^3 + 0 + C = 0\)، بنابراین \(C=0\)، و بدین ترتیب:
$$A_f(x)=\int_0^x (t^2 + 1 )dt=\frac{1}{3}x^3 + x + 0$$
مساحت گسترانیده شده از \(0\) تا \(3\) ـــ که ما آن را در فصل 14 به روش سخت محاسبۀ حد جمع ریمان انجام دادیم ـــ به سادگی \(A_f(3)\) است:
$$A_f(x)=\frac{1}{3}x^3 + x \\
A_f(3)=\frac{1}{3} \cdot 3^3 + 3 = 9 + 3 = 12 $$
به همین سادگی. این کار بسیار کمتری نسبت به انجام آن با روش سخت داشت.
و بعد از اینکه دانستید این تابع مساحت که در صفر آغاز می شود، \(\int_0^x (t^2+1)dt\)، برابر با \(\frac{1}{3}x^3 + x\) است، یافتن سایر مساحتهای زیر این سهمی که از صفر آغاز نمی شوند به سادگی یک بشکن زدن است. به عنوان مثال، فرض کنید، می خواهید مساحت زیر این سهمی را بین \(2\) و \(3\) بدست آورید. شما می توانید این مساحت را با تفریق مساحت بین \(0\) و \(2\) از مساحت بین \(0\) و \(3\) محاسبه کنید. شما اندکی پیش مساحت بین \(0\) و \(3\) را بدست آورده اید ـــ که \(12\) می باشد. و مساحت بین \(0\) و \(2\) برابر با \(A_f(2)=\frac{1}{3} \cdot 2^3 + 2 = 4\frac{2}{3}\) می باشد. بنابراین مساحت بین \(2\) و \(3\) برابر با \(12- 4 \frac{2}{3} = 7\frac{1}{3}\) می باشد.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: