خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
قضیۀ اساسی حسابان - نسخۀ دوم

اکنون ما سرانجام به میانبر عالیِ قضیۀ انتگرال گیری رسیده ایم که می توانید در بقیۀ عمرتان و یا دست کم تا انتهای دورۀ حسابانتان از آن استفاده کنید. این روش میانبر تمام چیزی است که برای مسأله های داستانیِ (word problems) موجود در فصلهای 17 و 18 به آن نیاز دارید.

این قضیه یک میانبر عالی برای محاسبۀ یک انتگرال معین (definite integral) مانند \(\int_2^3 (x^2+1)dx\)، مساحت زیر سهمیِ \(y=x^2+1\) بین \(2\) و \(3\)، به شما می دهد. همانطور که در بخش پیشین به شما نشان دادم، شما می توانید این مساحت را با تفریق مساحت بین \(0\) و \(2\) از مساحت بین \(0\) و \(3\) بدست آورید، اما برای انجام این کار نیاز دارید تا تابع مساحت خاصی که این مساحت را از صفر شروع به گسترانیدن می کند، بدانید:
$$\int_0^x (t^2+1)dt = \frac{1}{3}x^3+x+C$$
در اینجا مقدار \(C\) برابر با صفر می باشد.
زیباییِ این قضیۀ میانبر اینست که شما مجبور نیستید که حتی از یک تابع مساحت همچون \(A_f(x)=\int_0^x (t^2+1)dt\) استفاده کنید. شما صرفاً هر ضدمشتقی، \(F(x)\)، از تابعتان را می یابید و تفریق \(F(b)-F(a)\) را انجام می دهید. ساده ترین ضدمشتق برای استفاده، ضدمشتقی است که در آن \(C=0\) باشد. بنابراین، در اینجا چگونگی استفاده از این قضیه برای یافتن مساحت زیر این سهمی از \(2\) تا \(3\) را می بینید. \(F(x)=\frac{1}{3}x^3+x\) ضدمشتقی از \(x^2+1\) می باشد. سپس این قضیه نتیجۀ زیر را به شما می دهد:
$$\int_2^3 (x^2+1)dx = F(3)-F(2)$$
\(F(3)-F(2)\) می تواند به شکل زیر نوشته شود:
$$\biggl[\frac{1}{3}x^3+x \biggr]_2^3$$
بنابراین خواهیم داشت:
$$
\int_2^3 (x^2+1)dx = \biggl[\frac{1}{3}x^3+x \biggr]_2^3 \\
=\biggl( \frac{1}{3} \cdot 3^3 + 3 \biggr) - \biggl( \frac{1}{3} \cdot 2^3 + 2 \biggr) \\
= 12 - 4\frac{2}{3} \\
= 7 \frac{1}{3}
$$
می پذیرم، این همان محاسبه ای است که من در بخش پیشین با استفاده از تابع مساحت با \(s=0\) انجام دادم، اما آن صرفاً به دلیل تابع \(y=x^2+1\) زمانیکه \(s\) برابر با صفر و \(C\) نیز برابر با صفر است، می باشد. این به نوعی اتفاقی است، و برای تمامی توابع صدق نمی کند. اما صرفنظر از تابع، این میانبر درست جواب می دهد، و نیازی ندارید تا در مورد توابع مساحت برای \(s\) یا \(C\) نگران باشید. تمام کاری که شما باید انجام دهید \(F(b)-F(a)\) می باشد.
در اینجا مثال دیگری داریم: مساحت زیر تابع \(f(x)=e^x\) بین \(x=3\) و \(x=5\) چیست؟ مشتق \(e^x\) برابر با \(e^x\) است، بنابراین \(e^x\) ضدمشتقی از \(e^x\) می باشد، و بنابراین:
$$\int_3^5 e^x dx = \biggl[ e^x \biggr]_3^5 \\
= e^5 - e^3 \\
\approx 148.4 - 20.1 \\
\approx 128.3$$
به همین سادگی!
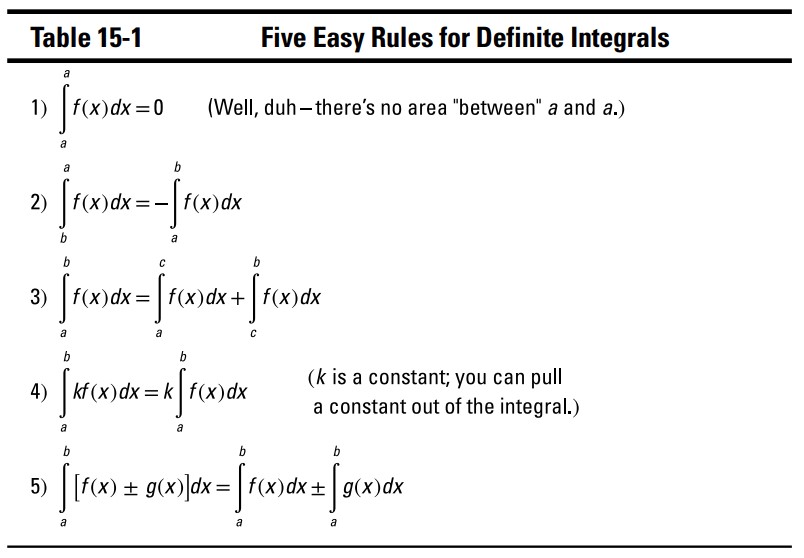
اوکی، شما هم اکنون این میانبر عالی را برای محاسبۀ مساحت زیر یک منحنی دارید. و اگر یک میانبر بزرگ برای اینکه روز شما را بسازد کفایت نکند، جدول 1-15 چندین قانون در مورد انتگرال های معین را لیست کرده است که می تواند زندگی شما را بسیار ساده تر کند.
حالا که نسخۀ میانبر قضیۀ اساسی حسابان را به شما دادم، بدین معنا نیست که به طور کامل از وضعیت دشوار فرار کرده اید. در ادامه سه روش مختلف برای درک اینکه چرا این قضیه درست کار می کند، آمده است. اینها چیزهای دشواری هستند ـــ خودتان را برای مواجهه با آنها آماده کنید.
از سوی دیگر، اگر تنها چیزی که بدنبالش هستید چگونگی محاسبۀ یک مساحت می باشد، می توانید این توضیحات را نادیده بگیرید: \(C\) را فراموش کنید و صرفاً \(F(a)\) را از \(F(b)\) تفریق کنید. من این توضیحات را به این دلیل گنجانده ام که گمان می کنم شما می خواهید ریاضی را صرفاً برای عشق به یادگیری بیاموزید ـــ آیا اینطور نیست؟ کتابهای دیگر صرفاً قوانین را به شما می دهند؛ من توضیح می دهم که چرا آنها درست کار می کنند و به اصول اساسی آنها می پردازم.
در واقع، جدای از شوخی، شما باید دست کم قدری از این موضوعات را بخوانید. قضیۀ اساسی حسابان (fundamental theorem of calculus) یکی از مهمترین قضایایِ تمامی ریاضیات می باشد، بنابراین شما باید زمانی را صرف تلاش سخت برای درک اینکه این قضیه در چه مورد است، بکنید. به تلاشش می ارزد. از این سه توضیح، اولی ساده ترین است. اما اگر فقط قصد دارید که یک یا دو تا از این توضیحات را بخوانید، فقط سومی را بخوانید، یا دومی و سومی را. در نهایت اگر نتوانید در مرحلۀ اول خواندن آنها را درک کنید هیچ نگران نباشید، شما می توانید بعداً دوباره به آنها مراجعه کنید.
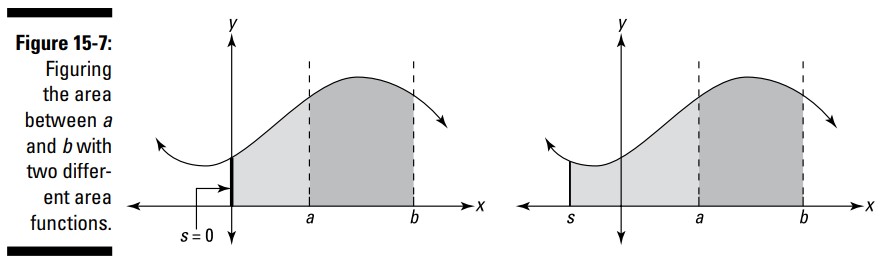
یک روش برای درک نسخۀ میانبر قضیۀ اساسی حسابان اینست که به توابع مساحت بنگرید. همانطور که در شکل 7-15 می بینید، مساحت تیره شده بین \(a\) و \(b\) می تواند با آغاز کردن با مساحت بین \(s\) و \(b\)، سپس برش دادن (تفریق) مساحت بین \(s\) و \(a\)، بدست آید. و مهم نیست که آیا شما \(0\) را بعنوان لبۀ چپ از مساحتها یا هر مقدار دیگری از \(s\) مورد استفاده قرار دهید. آیا می بینید که چه از نمودار سمت چپ و چه از نمودار سمت راست استفاده کنید، به نتیجۀ یکسانی می رسید؟
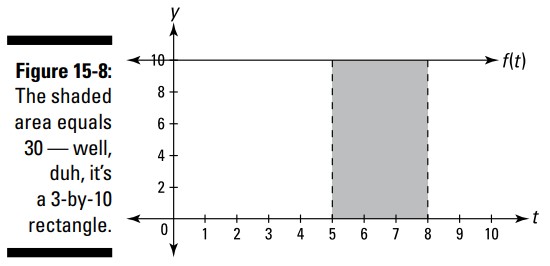
به \(f(t)=10\) نگاهی بیندازید (شکل 8-15 را ببینید). فرض کنید که مساحت بین \(5\) و \(8\) در زیر خط افقیِ \(f(t)=10\) را می خواهید، و مجبور هستید که از حسابان استفاده کنید.
به دو تا از توابع مساحت برای \(f(t)=10\) در شکل 5-15 بازگردید: \(A_f(x)\) در \(0\) آغاز می شود (که در آن \(C=0\)) و \(B_f(x)\) در \(-2\) آغاز می شود (که در آن \(C=20\)):
$$A_f(x)=\int_0^x 10dt=10x \\
B_f(x)=\int_{-2}^x 10dt=10x + 20 $$
اگر از \(A_f(x)\) برای محاسبۀ مساحت بین \(5\) و \(8\) در شکل 8-15 استفاده کنید، به نتیجۀ زیر می رسید:
$$\int_5^8 10dx=A_f(8) - A_f(5) \\
=10 \cdot 8 - 10 \cdot 5 \\
= 80 - 50 \\
=30$$
(\(80\) مساحت مستطیل بین \(0\) تا \(8\) می باشد؛ \(50\) مساحت مستطیل بین \(0\) تا \(5\) می باشد.)
از سوی دیگر، اگر از \(B_f(x)\) برای محاسبۀ همان مساحت استفاده کنید، به نتیجۀ یکسانی می رسید:
$$\int_5^8 10dx=B_f(8) - B_f(5) \\
=(10 \cdot 8 + 20) - (10 \cdot 5 + 20) \\
=(80 + 20) - (50 + 20) \\
=100-70 \\
= 30$$
(\(100\) مساحت مستطیلِ بین \(-2\) تا \(8\) می باشد؛ \(70\) مساحت مستطیلِ بین \(-2\) تا \(5\) می باشد.)
توجه داشته باشید که دو \(20\) موجود در خط سوم، یکدیگر را خنثی می کنند. بیاد بیاورید که تمامی ضدمشتق های \(f(t)=10\) در شکل \(10x+C\) می باشند. صرفنظر از مقدار \(C\)، آنها همدیگر را مانند این مثال خنثی می کنند. بنابراین شما می توانید از هر ضدمشتقی با هر مقداری از \(C\) استفاده کنید. برای راحتی، همه صرفاً از ضدمشتقی که در آن \(C=0\) استفاده می کنند، بنابراین به هیچ وجه لازم نیست که با \(C\) کارتان را شلوغتر کنید. و انتخاب \(s\) (جاییکه تابع مساحت در آن آغاز می گردد) غیرضروری است. بنابراین هنگامی که از نسخۀ میانبرِ قضیۀ اساسی حسابان استفاده می کنید، و مساحت را با \(F(b)-F(a)\) محاسبه می کنید، به نوعی از یک تابع مساحت رمزآلود با مقدار \(C\) صفر و نقطۀ آغاز نامشخص، \(s\)، استفاده می کنید. متوجه شدید؟
توضیح بعدی از نسخۀ میانبر قضیۀ اساسی حسابان شامل ارتباط یین/یانگ (yin/yang relationship) بین مشتق گیری و انتگرال گیری می باشد. شکل 9-15 را بررسی کنید.
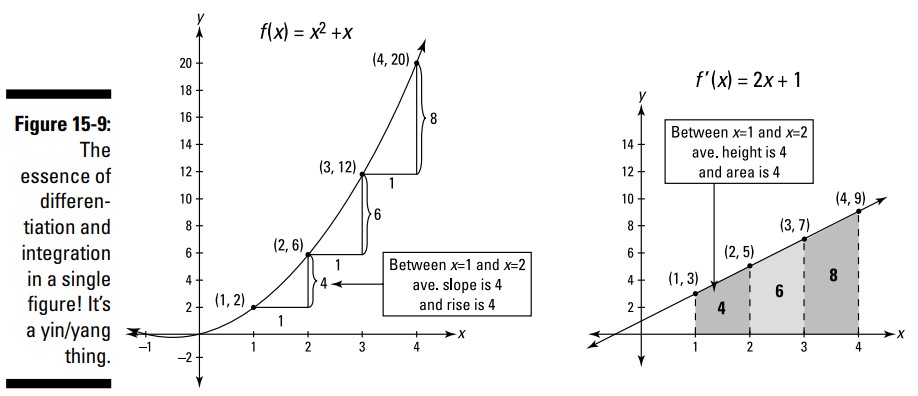
این شکل تابع \(f(x)=x^2+x\) و مشتق آن، \(f'(x)=2x+1\)، را نشان می دهد. با دقت به اعداد \(4\)، \(6\)، و \(8\) بر روی هر دو نمودار نگاه کنید. ارتباط بین \(4\)، \(6\)، و \(8\) بر روی نمودار \(f\) ـــ که مقادیر بالا رفتن بین نقاط متوالیِ بر روی این منحنی می باشند ـــ و \(4\)، \(6\)، و \(8\) بر روی نمودار \(f'\) ـــ که مساحت های ذوزنقه های زیر \(f'\) می باشند ـــ ارتباط صمیمیِ بین انتگرال گیری و مشتق گیری را نشان می دهند. شکل 9-15 از آن تصاویری است که به قول معروف برابر هزار کلمه می ارزند، این شکل جوهرۀ انتگرال گیری را در یک عکس آنی نشان می دهد. این شکل نشان می دهد چگونه نسخۀ میانبر قضیۀ اساسی حسابان درست کار می کند زیرا نشان می دهد که مساحت زیر \(f'(x)\) بین \(1\) و \(4\) برابر است با مجموع بالا رفتن بر روی \(f(x)\) بین \((1,2)\) و\((4,20)\)، به عبارت دیگر:
$$\int_1^4 f'(x)=f(4)-f(1)$$
توجه داشته باشید که من این دو تابع موجود در شکل 9-15 و معادلۀ بالا را \(f\) و \(f'\) نامیده ام تا روی این نکته تاکید کنم که \(2x+1\) مشتق \(x^2+x\) می باشد. من می توانستم به جای این کار به \(x^2+x\) به عنوان \(F\) و به \(2x+1\) به عنوان \(f\) اشاره کنم که در آن صورت روی این نکته تاکید می شد که \(x^2+x\) ضدمشتقی از \(2x+1\) می باشد. در آن صورت شما این معادلۀ مساحت بالا را در شکل استانداردش می نوشتید:
$$\int_1^4 f(x)dx=F(4)-F(1)$$
در هر دو صورت، معنا یکسان است. من از نسخۀ مشتق استفاده کردم تا اشاره کنم چگونه یافتن مساحت برابر با معکوس مشتق گیری می باشد. حرکت از سمت چپ به سمت راست در شکل 9-15 برابر با مشتق گیری می باشد: شیب های \(f\) با ارتفاع های \(f'\) متناظر می باشند. حرکت از سمت راست به چپ انتگرال گیری می باشد: مساحت های زیر \(f'\) با تغییر در ارتفاع بین دو نقطۀ موجود بر روی \(f\) متناظر می باشند.
اوکی، در اینجا چگونگی کارکرد آن را می بینید. تصور کنید در امتداد \(f\) از \((1,2)\) تا \((2,6)\) بالا می روید. هر نقطه در امتداد این مسیر دارای تندی (شیب) خاصی می باشد. این شیب (slope) به عنوان مختصات \(y\)، یا ارتفاع، بر روی نمودار \(f'\) ترسیم شده است. این واقعیت که \(f'\) از \((1,3)\) تا \((2,5)\) بالا می رود، به شما می گوید همینطور که بین \((1,2)\) و \((2,6)\) سفر می کنید، شیب \(f\) از \(3\) تا \(5\) بالا می رود. همۀ اینها از مبانی مشتق گیری پیروی می کنند.
اکنون، همینطور که در امتداد \(f\) از \((1,2)\) تا \((2,6)\) پیش می روید، این شیب به طور مداوم تغییر می کند. اما معلوم می شود از آنجا که به ازاء هر \(1\) واحدی که پیش می روید، \(4\) واحد بالا می روید، میانگین تمامی شیب های \(f\) بین \((1,2)\) و \((2,6)\) برابر با \(\frac{4}{1}\) یا \(4\) می باشد. از آنجا که هر کدام از این شیب ها، بر روی \(f'\) به عنوان مختصات \(y\) یا ارتفاع، ترسیم شده اند، نتیجه می شود که میانگین ارتفاع \(f'\) بین \((1,3)\) و \((2,5)\) نیز برابر با \(4\) می باشد. بنابراین، بین این دو نقطۀ داده شده، میانگین شیب بر روی \(f\) با میانگین ارتفاع بر روی \(f'\) برابر می باشند.
صبر کنید، شما تقریباً به هدف رسیده اید. شیب برابر با \(\frac{\text{rise}}{\text{run}}\) می باشد، بنابراین هنگامی که run برابر با \(1\) باشد، شیب برابر با rise می باشد. به عنوان مثال، از \((1,2)\) تا \((2,6)\) بر روی \(f\)، این منحنی \(4\) واحد بالا می رود و میانگین شیب بین آن نقاط نیز برابر با \(4\) می باشد. بنابراین، بین هر دو نقطه ای بر روی \(f\) که مختصات \(x\) آن \(1\) واحد با یکدیگر فرق داشته باشند، میانگین شیب برابر با rise می باشد.
مساحت یک ذوزنقه (trapezoid) مانند آنهایی که در سمت راست شکل 9-15 می بینید، برابر با عرض آن ضربدر میانگین ارتفاع آن می باشد. (این فرمول برای هر شکل مشابه دیگری که دارای انتهایی همانند یک مستطیل باشد، صدق می کند؛ بالای آن می تواند هر خط کج یا هر منحنی غیرمعمولی باشد که شما دوست داشته باشید.) بنابراین، از آنجا که عرض هر ذوزنقه برابر با \(1\) است، و از آنجا که هر چیزی ضربدر \(1\) برابر با خودش می شود، میانگین ارتفاع هر ذوزنقۀ زیر \(f'\) مساحت آن می باشد؛ به عنوان نمونه، مساحت ذوزنقۀ اول برابر با \(4\) و میانگین ارتفاع آن نیز برابر با \(4\) می باشد.
آیا برای فینال بزرگ آماده هستید؟ در اینجا کل این استدلال را به صورت خلاصه داریم. بر روی \(f\)، \(\text{rise}=\text{average slope}\)؛ وقتی از \(f\) به \(f'\) برویم، \(\text{average slope} = \text{average height}\)؛ بر روی \(f'\)، \(\text{average height} = \text{area}\). بنابراین، نتیجه می شود \(\text{rise} = \text{slope} = \text{height} = \text{area}\)، و بدین ترتیب، در نهایت، \(\text{rise}=\text{area}\). و این چیزی است که نسخۀ دوم قضیۀ اساسی حسابان بیان می دارد:
$$f(b)-f(a)=\int_a^b f'(x)dx \\
\text{rise} = \text{area}$$
این مفاهیم به طرز اجتناب ناپذیری دشوار می باشند. شما ممکن است مجبور شوید دو یا سه مرتبه آن را بخوانید تا درعمق آن فرو بروید.
توجه داشته باشید که اگر هر تابع دیگری از شکل \(x^2+x+C\) را به جای \(x^2 + x\) استفاده کنید، در ارتباط بین شیب و مساحت هیچ تفاوتی ایجاد نمی کند. هر سهمی مانند \(x^2+x+10\) یا \(x^2+x-5\) دقیقاً شکل یکسانی با \(x^2+x\) دارد؛ آن صرفاً به صورت عمودی به سمت بالا یا پایین می لغزد. هر سهمی مشابه دیگری، دقیقاً به شیوۀ یکسانی با سهمی موجود در شکل 9-15، بین \(x=1\) و \(x=4\) بالا می رود. از \(1\) تا \(2\) ، این سهمی ها \(1\) واحد رو به جلو و \(4\) واحد رو به بالا می روند. از \(2\) تا \(3\)، آنها \(1\) رو به جلو و \(6\) رو به بالا می روند، وبه همین ترتیب. به همین دلیل هم است که از هر ضدمشتقی می توانید برای یافتن مساحت استفاده کنید. مجموع مساحت زیر \(f'\) بین \(1\) و \(4\)، یعنی \(18\)، با مجموع بالا رفتن بر روی هر کدام از این سهمی ها از \(1\) تا \(4\)، یعنی \(4+6+8=18\) برابر می باشد.
با پذیرش این ریسک که ممکن است آب در هاون بکوبم، توضیحات سوم مربوط به قضیۀ اساسی حسابان را برای شما می آورم. شما ممکن است آن را بر دو توضیح اول ترجیح بدهید، زیرا کمتر انتزاعی می باشد ـــ آن براساس مفاهیم ساده و مبتنی بر فهم عمومی، که ما در زندگی روزمره با آنها برخورد داریم می باشد. این توضیح با توضیح قبلی چیزهای مشترک بسیاری دارد، اما مفاهیم ارائه شده در آن از زاویه ای دیگر مورد بررسی قرار گرفته اند.
اجازه ندهید عنوان این بخش منجر شود شما مطالعۀ آن را به زمان دیگری موکول کنید. من درک می کنم که بسیاری از خوانندگان این کتاب حسابان ممکن است هنوز آمار (statistics) را مطالعه نکرده باشند. نگران نباشید؛ ارتباط با آماری که در زیر توضیح داده ام شامل یک چیز خیلی ساده است که در دوره های آمار پوشش داده شده است، اما برای درک این مفهوم به هیچ وجه نیازی ندارید که آمار بدانید. این مفهوم ساده ارتباط بین یک نمودار توزیع فراوانی (frequency distribution graph) و یک نمودار توزیع فراوانی تجمعی (cumulative frequency distribution graph) می باشد (شما ممکن است در یک روزنامه یا مجله با چنین نمودارهایی روبرو شده باشید). شکل 10-15 را در نظر بگیرید.
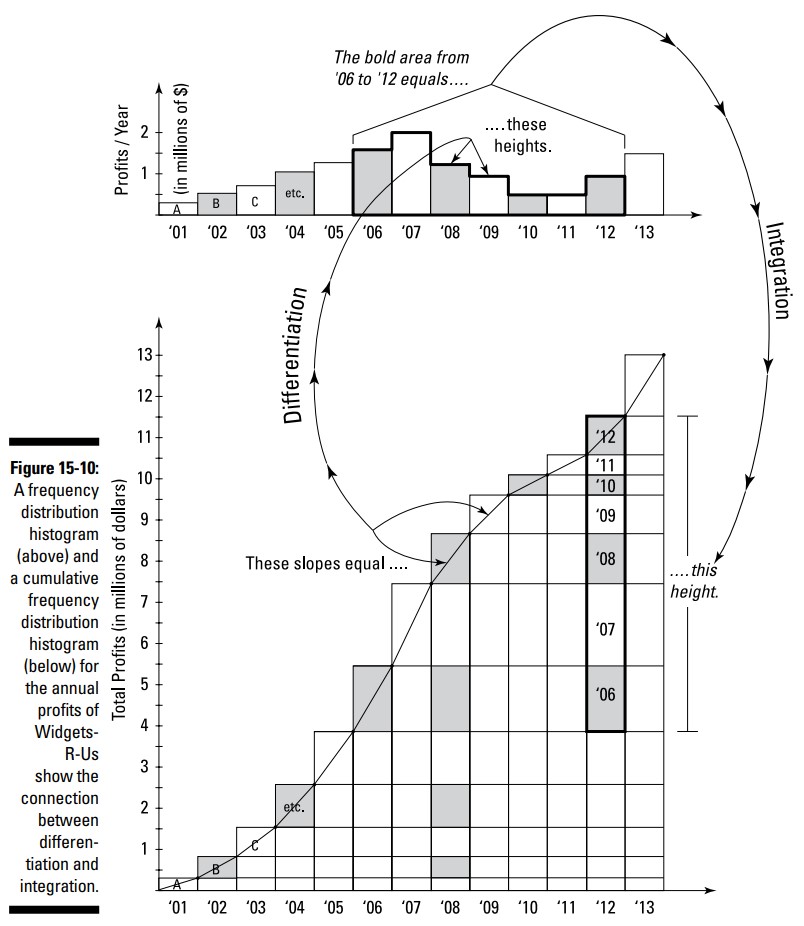
نمودار بالایی در این شکل یک نمودار ستونی (هیستوگرام/histogram) از سود سالانه از شرکت Widgets-R-Us را از 1 ژانویۀ 2001 تا 31 دسامبر 2013 نشان می دهد. به عنوان مثال، مستطیل نشان گذاری شده با \(07\) نشان می دهد که سود این شرکت برای 2007 برابر با \($2,000,000\) بوده است (سال 2007 بهترین سال آنها در طول \(\text{2001-2013}\) می باشد).
نمودار پایینی در این شکل یک نمودار ستونی (هیستوگرام) توزیع فراوانی تجمعی برای همان داده ها می باشد که در نمودار بالایی مورد استفاده قرار گرفته اند. تفاوت به سادگی در اینست که در نمودار تجمعی، ارتفاع هر ستون، سود بدست آمده از \(\text{1/1/2001}\) را نشان می دهد. به عنوان مثال، به ستون \(02\) در نمودار پایین و مستطیل های \(01\) و \(02\) در نمودار بالا نگاه کنید. شما می توانید ببینید که ستون \(02\) یک مستطیل \(02\) را نشان می دهد که بر روی یک مستطیل \(01\) نشسته است که منجر می شود ستون \(02\) دارای ارتفاعی برابر با مجموع سودهای \(01\) و \(02\) باشد. متوجه شدید؟ همینطور که به سمت راست نمودار تجمعی پیش می روید، ارتفاع هر ستون متوالی به سادگی به میزان سودهای بدست آمده در سالهای مجزای متناظر نمایش داده شده در نمودار بالایی، رشد می کند.
اوکی. پس ارتباط حسابان آن را در اینجا می بینید. (شکیبایی کنید؛ اندکی طول می کشد تا گام به گام در این فرآیندها پیش برویم.) به مستطیل بالایی در ستون \(08\) بر روی نمودار تجمعی بنگرید (بیایید برای خلاصه سازی این نمودار را \(C\) بنامیم). در این مرحله، بر روی \(C\) شما \(1\) سال رو به جلو می روید (run)، و معادل \($1,250,000\) رو به بالا می روید (up)، سود \(08\) را بر روی نمودار توزیع می بینید (به نمودار بالا با \(F\) اشاره می کنیم). ما می دانیم که شیب برابر است با \(\frac{\text{rise}}{\text{run}}\)، بنابراین از آنجا که run برابر با \(1\) می باشد، شیب برابر با \(\frac{1,250,000}{1}\) یا فقط \(1,250,000\) می باشد، که مسلماً همان rise است. بدین ترتیب، شیب بر روی \(C\) (در \(08\) یا هر سال دیگر) می تواند به عنوان ارتفاع بر روی \(F\) برای سال متناظرش، خوانده شود. (مطمئن شوید که چگونگی کارکرد آن را بدانید.) از آنجا که ارتفاع ها (یا مقادیر تابع) بر روی \(F\) شیب های \(C\) می باشند، \(F\) مشتق \(C\) می باشد. به طور خلاصه، \(F\)، مشتق، در مورد شیب \(C\) به ما می گوید.
مفهوم بعدی اینست، از آنجا که \(F\) مشتقی از \(C\) می باشد، بنابه تعریف، \(C\) ضدمشتقی از \(F\) است (به عنوان مثال، \(C\) ممکن است برابر با \(5x^3\) و \(F\) برابر با \(15x^2\) باشد). حالا، \(C\)، ضدمشتق \(F\)، در مورد \(F\) به ما چه می گوید؟ تصور کنید، یک خط عمودی از چپ به راست بر روی \(F\) بکشید. همینطور که در \(F\) از روی این مستطیل ها ـــ سال به سال ـــ عبور می کنید مجموع کل مساحتی که از روی آن عبور می کنید در امتداد \(C\) به صورت بالا رفتن نشان داده می شود.
به مستطیل های \(01\) تا \(08\) بر روی \(F\) بنگرید. شما می توانید آن مستطیل های یکسان را که به صورت پلکانی در امتداد \(C\) بالا می روند را ببینید (مستطیل هایی را که با \(A\)، \(B\)، \(C\) و \(etc.\) نامگذاری شده اند را بر روی هر دو نمودار ببینید). همینطور که بر روی این شکل پلکانی بالا می روید، ارتفاع های مستطیل های \(F\) بر روی \(C\) با یکدیگر جمع می شوند. و من نشان داده ام که چگونه مستطیل های یکسان \(01\) تا \(08\) که در امتداد بالای پلکانی \(C\) قرار گرفته اند، نیز می توانند در سال \(08\) بر روی \(C\) به شکل یک پشتۀ عمودی دیده شوند. من نمودار تجمعی را به این شیوه ترسیم کرده ام تا حتی بیش از پیش نمایان شود که ارتفاع مستطیل ها با یکدیگر جمع می شوند. (توجه: بیشتر نمودارهای ستونی تجمعی اینگونه ترسیم نمی شوند.)
هر مستطیل بر روی \(F\) دارای پایه ای از \(1\) سال می باشد، بنابراین، از آنجا که \(\text{area} = \text{base} \times \text{height}\)، مساحت هر مستطیل برابر با ارتفاع آن می باشد. بنابراین، همینطور که این مستطیل ها را در \(C\) بر روی هم انباشته می کنید، مساحت های آن مستطیل های موجود در \(F\) را با یکدیگر جمع می کنید. به عنوان مثال، ارتفاع مستطیل های انباشته شده از \(01\) تا \(08\) بر روی \(F\) \(($ 8.5 \text{ million})\) برابر با مجموع مساحت مستطیل های \(01\) تا \(08\) بر روی \(F\) می باشد. و بنابراین، ارتفاع یا مقادیر تابع در \(C\) ـــ که ضدمشتق \(F\) می باشد ـــ مساحت زیر لبۀ بالای \(F\) را به شما می دهد. این چگونگی کارکرد انتگرال گیری می باشد.
اوکی، ما تقریباً کار را انجام دادیم. حالا به سراغ این مسأله می رویم که چگونه این دو نمودار نسخۀ میانبر قضیۀ اساسی حسابان و ارتباط بین مشتق گیری و انتگرال گیری را توصیف می کنند. به مستطیل های \(06\) تا \(12\) بر روی \(F\) بنگرید (که دارای حاشیۀ پررنگ می باشند). شما می توانید مستطیل های یکسانی با آنها را در بخش پررنگ شده در ستون \(12\) از \(C\) ببینید. ارتفاع آن پشتۀ پررنگ شده، که مجموع سود بدست آمده در طول آن \(7\) سال را نشان می دهد، \($7.75 \text{ million}\)، برابر با مجموع مساحت این \(7\) مستطیل بر روی \(F\) می باشد. و برای بدست آوردن ارتفاع این پشته بر روی \(C\)، شما به سادگی ارتفاع لبۀ پایینی این پشتۀ را از ارتفاع لبۀ بالایی آن تفریق می کنید. این در واقع تمامی چیزی است که نسخۀ میانبر قضیۀ اساسی حسابان بیان می دارد: مساحت زیر هر بخشی از هر تابعی (مانند \(F\)) با تغییر در ارتفاع ضدمشتق آن تابع (مانند \(C\)) بدست می آید.
به طور خلاصه (به نگاه کردن به آن مستطیل های دارای حاشیۀ پررنگ بر روی هر دو نمودار ادامه دهید)، شیب های مستطیل ها بر روی \(C\) به عنوان ارتفاع ها در \(F\) نمایان می شوند. این مشتق گیری است. در جهت معکوس، شما انتگرال گیری را می بینید: تغییر در ارتفاع ها بر روی \(C\) مساحت زیر \(F\) را نشان می دهد. مشتق گیری و انتگرال گیری دو روی یک سکه هستند.
توجه: ریاضیدانان محض ممکن است به این توضیح از قضیۀ اساسی حسابان اعتراض داشته باشند زیرا شامل نمودارهای گسسته می باشد (به عنوان مثال، این حقیقت که نمودار ستونی توزیع فراوانی تجمعی در شکل 10-15 در افزایش هر یک سال بالا می رود)، در حالیکه حسابان مطالعۀ نمودارهایی می باشد که به صورت نرم و مداوم تغییر می کنند (نسخۀ حسابانی از نمودار ستونی توزیع فراوانی تجمعی می تواند یک منحنی نرم باشد که مجموع رشد سود را در هر میلی ثانیه نشان می دهد ـــ در واقع، به لحاظ نظری، در هر کسر بی نهایت کوچک از ثانیه). اوکی ـــ به اعتراض اشاره شد ـــ اما واقعیت اینست که توضیحاتی که در اینجا ارائه شد به درستی نشان می دهند که چگونه انتگرال گیری و مشتق گیری با یکدیگر مرتبطند و به درستی نشان می دهند که نسخۀ میانبر قضیۀ اساسی حسابان چگونه کار می کند. تمام کاری که برای تبدیل شکل 10-15 و توضیحات همراه آن به حسابان استاندارد باید انجام بدهید اینست که همه چیز را به حد ببرید، بازۀ سود را کوتاهتر و کوتاهتر و باز هم کوتاهتر کنید: از یک سال به یک ماه به یک روز و ... . با حد، نمودارهای گسستۀ موجود در شکل 10-15 به نمودارهای نرم حسابانی تبدیل می شوند. اما مفاهیم تغییر نمی کند. مفاهیم دقیقاً همانهایی خواهند بود که در اینجا توضیح داده شدند.
خوب، به همین سادگی ـــ توضیحات واقعی برای اینکه چرا نسخۀ میانبر قضیۀ اساسی حسابان به درستی کار می کند و چرا یافتن مساحت معکوس مشتق گیری می باشد. اگر فقط نیمی از آنچه را که نوشتم درک کردید، از بیشتر دانش آموزان حسابان جلوترید. خبر خوب اینست که به احتمال زیاد از این چیزهای تئوری از شما امتحانی گرفته نمی شود. حالا بیایید دوباره به کرۀ زمین باز گردیم.

قضیۀ اصلی حسابان (fundamental theorem of calculus) نسخۀ دوم یا نسخۀ میانبر: فرض کنید \(F\) هر ضدمشتقی از تابع \(f\) باشد؛ آن گاه:
$$\int_a^b f(x)dx=F(b)-F(a)$$
$$\int_a^b f(x)dx=F(b)-F(a)$$
این قضیه یک میانبر عالی برای محاسبۀ یک انتگرال معین (definite integral) مانند \(\int_2^3 (x^2+1)dx\)، مساحت زیر سهمیِ \(y=x^2+1\) بین \(2\) و \(3\)، به شما می دهد. همانطور که در بخش پیشین به شما نشان دادم، شما می توانید این مساحت را با تفریق مساحت بین \(0\) و \(2\) از مساحت بین \(0\) و \(3\) بدست آورید، اما برای انجام این کار نیاز دارید تا تابع مساحت خاصی که این مساحت را از صفر شروع به گسترانیدن می کند، بدانید:
$$\int_0^x (t^2+1)dt = \frac{1}{3}x^3+x+C$$
در اینجا مقدار \(C\) برابر با صفر می باشد.
زیباییِ این قضیۀ میانبر اینست که شما مجبور نیستید که حتی از یک تابع مساحت همچون \(A_f(x)=\int_0^x (t^2+1)dt\) استفاده کنید. شما صرفاً هر ضدمشتقی، \(F(x)\)، از تابعتان را می یابید و تفریق \(F(b)-F(a)\) را انجام می دهید. ساده ترین ضدمشتق برای استفاده، ضدمشتقی است که در آن \(C=0\) باشد. بنابراین، در اینجا چگونگی استفاده از این قضیه برای یافتن مساحت زیر این سهمی از \(2\) تا \(3\) را می بینید. \(F(x)=\frac{1}{3}x^3+x\) ضدمشتقی از \(x^2+1\) می باشد. سپس این قضیه نتیجۀ زیر را به شما می دهد:
$$\int_2^3 (x^2+1)dx = F(3)-F(2)$$
\(F(3)-F(2)\) می تواند به شکل زیر نوشته شود:
$$\biggl[\frac{1}{3}x^3+x \biggr]_2^3$$
بنابراین خواهیم داشت:
$$
\int_2^3 (x^2+1)dx = \biggl[\frac{1}{3}x^3+x \biggr]_2^3 \\
=\biggl( \frac{1}{3} \cdot 3^3 + 3 \biggr) - \biggl( \frac{1}{3} \cdot 2^3 + 2 \biggr) \\
= 12 - 4\frac{2}{3} \\
= 7 \frac{1}{3}
$$
می پذیرم، این همان محاسبه ای است که من در بخش پیشین با استفاده از تابع مساحت با \(s=0\) انجام دادم، اما آن صرفاً به دلیل تابع \(y=x^2+1\) زمانیکه \(s\) برابر با صفر و \(C\) نیز برابر با صفر است، می باشد. این به نوعی اتفاقی است، و برای تمامی توابع صدق نمی کند. اما صرفنظر از تابع، این میانبر درست جواب می دهد، و نیازی ندارید تا در مورد توابع مساحت برای \(s\) یا \(C\) نگران باشید. تمام کاری که شما باید انجام دهید \(F(b)-F(a)\) می باشد.
در اینجا مثال دیگری داریم: مساحت زیر تابع \(f(x)=e^x\) بین \(x=3\) و \(x=5\) چیست؟ مشتق \(e^x\) برابر با \(e^x\) است، بنابراین \(e^x\) ضدمشتقی از \(e^x\) می باشد، و بنابراین:
$$\int_3^5 e^x dx = \biggl[ e^x \biggr]_3^5 \\
= e^5 - e^3 \\
\approx 148.4 - 20.1 \\
\approx 128.3$$
به همین سادگی!
مساحت های بالای منحنی و زیر محور \(x\) به عنوان مساحت های منفی محاسبه می شوند. قبل از اینکه ادامه بدهیم، من بابت این غفلت که به مساحت های منفی اشاره نکرده بودم، پوزش می خواهم (این تقریباً همان هشداری است که در اواخر فصل 14 به آن اشاره کردم.) توجه داشته باشید که دو مثال بالا، سهمیِ \(y=x^2+1\)، و تابع نمایی \(y=e^x\)، مساحت های محاسبه شده زیر منحنی و بالای محور \(x\) می باشند. این مساحت ها به عنوان مساحت های معمولیِ مثبت در نظر گرفته می شوند. اما اگر تابعی زیر محور \(x\) برود، مساحت های بالای منحنی و زیر محور \(x\) به عنوان مساحت های منفی در نظر گرفته می شوند. خواه اینکه از یک تابع مساحت استفاده کنید، یا از اولین نسخۀ قضیۀ اساسی حسابان استفاده کنید، و یا از نسخۀ میانبر آن استفاده کنید، تفاوتی نمی کند و این مسأله برقرار است. فعلاً در مورد این نگران نباشید. در فصل 17 خواهید دید که چگونه کار می کند.
اوکی، شما هم اکنون این میانبر عالی را برای محاسبۀ مساحت زیر یک منحنی دارید. و اگر یک میانبر بزرگ برای اینکه روز شما را بسازد کفایت نکند، جدول 1-15 چندین قانون در مورد انتگرال های معین را لیست کرده است که می تواند زندگی شما را بسیار ساده تر کند.

حالا که نسخۀ میانبر قضیۀ اساسی حسابان را به شما دادم، بدین معنا نیست که به طور کامل از وضعیت دشوار فرار کرده اید. در ادامه سه روش مختلف برای درک اینکه چرا این قضیه درست کار می کند، آمده است. اینها چیزهای دشواری هستند ـــ خودتان را برای مواجهه با آنها آماده کنید.
از سوی دیگر، اگر تنها چیزی که بدنبالش هستید چگونگی محاسبۀ یک مساحت می باشد، می توانید این توضیحات را نادیده بگیرید: \(C\) را فراموش کنید و صرفاً \(F(a)\) را از \(F(b)\) تفریق کنید. من این توضیحات را به این دلیل گنجانده ام که گمان می کنم شما می خواهید ریاضی را صرفاً برای عشق به یادگیری بیاموزید ـــ آیا اینطور نیست؟ کتابهای دیگر صرفاً قوانین را به شما می دهند؛ من توضیح می دهم که چرا آنها درست کار می کنند و به اصول اساسی آنها می پردازم.
در واقع، جدای از شوخی، شما باید دست کم قدری از این موضوعات را بخوانید. قضیۀ اساسی حسابان (fundamental theorem of calculus) یکی از مهمترین قضایایِ تمامی ریاضیات می باشد، بنابراین شما باید زمانی را صرف تلاش سخت برای درک اینکه این قضیه در چه مورد است، بکنید. به تلاشش می ارزد. از این سه توضیح، اولی ساده ترین است. اما اگر فقط قصد دارید که یک یا دو تا از این توضیحات را بخوانید، فقط سومی را بخوانید، یا دومی و سومی را. در نهایت اگر نتوانید در مرحلۀ اول خواندن آنها را درک کنید هیچ نگران نباشید، شما می توانید بعداً دوباره به آنها مراجعه کنید.
چرا این قضیه درست کار می کند: توضیحات توابع مساحت
یک روش برای درک نسخۀ میانبر قضیۀ اساسی حسابان اینست که به توابع مساحت بنگرید. همانطور که در شکل 7-15 می بینید، مساحت تیره شده بین \(a\) و \(b\) می تواند با آغاز کردن با مساحت بین \(s\) و \(b\)، سپس برش دادن (تفریق) مساحت بین \(s\) و \(a\)، بدست آید. و مهم نیست که آیا شما \(0\) را بعنوان لبۀ چپ از مساحتها یا هر مقدار دیگری از \(s\) مورد استفاده قرار دهید. آیا می بینید که چه از نمودار سمت چپ و چه از نمودار سمت راست استفاده کنید، به نتیجۀ یکسانی می رسید؟

به \(f(t)=10\) نگاهی بیندازید (شکل 8-15 را ببینید). فرض کنید که مساحت بین \(5\) و \(8\) در زیر خط افقیِ \(f(t)=10\) را می خواهید، و مجبور هستید که از حسابان استفاده کنید.

به دو تا از توابع مساحت برای \(f(t)=10\) در شکل 5-15 بازگردید: \(A_f(x)\) در \(0\) آغاز می شود (که در آن \(C=0\)) و \(B_f(x)\) در \(-2\) آغاز می شود (که در آن \(C=20\)):
$$A_f(x)=\int_0^x 10dt=10x \\
B_f(x)=\int_{-2}^x 10dt=10x + 20 $$
اگر از \(A_f(x)\) برای محاسبۀ مساحت بین \(5\) و \(8\) در شکل 8-15 استفاده کنید، به نتیجۀ زیر می رسید:
$$\int_5^8 10dx=A_f(8) - A_f(5) \\
=10 \cdot 8 - 10 \cdot 5 \\
= 80 - 50 \\
=30$$
(\(80\) مساحت مستطیل بین \(0\) تا \(8\) می باشد؛ \(50\) مساحت مستطیل بین \(0\) تا \(5\) می باشد.)
از سوی دیگر، اگر از \(B_f(x)\) برای محاسبۀ همان مساحت استفاده کنید، به نتیجۀ یکسانی می رسید:
$$\int_5^8 10dx=B_f(8) - B_f(5) \\
=(10 \cdot 8 + 20) - (10 \cdot 5 + 20) \\
=(80 + 20) - (50 + 20) \\
=100-70 \\
= 30$$
(\(100\) مساحت مستطیلِ بین \(-2\) تا \(8\) می باشد؛ \(70\) مساحت مستطیلِ بین \(-2\) تا \(5\) می باشد.)
توجه داشته باشید که دو \(20\) موجود در خط سوم، یکدیگر را خنثی می کنند. بیاد بیاورید که تمامی ضدمشتق های \(f(t)=10\) در شکل \(10x+C\) می باشند. صرفنظر از مقدار \(C\)، آنها همدیگر را مانند این مثال خنثی می کنند. بنابراین شما می توانید از هر ضدمشتقی با هر مقداری از \(C\) استفاده کنید. برای راحتی، همه صرفاً از ضدمشتقی که در آن \(C=0\) استفاده می کنند، بنابراین به هیچ وجه لازم نیست که با \(C\) کارتان را شلوغتر کنید. و انتخاب \(s\) (جاییکه تابع مساحت در آن آغاز می گردد) غیرضروری است. بنابراین هنگامی که از نسخۀ میانبرِ قضیۀ اساسی حسابان استفاده می کنید، و مساحت را با \(F(b)-F(a)\) محاسبه می کنید، به نوعی از یک تابع مساحت رمزآلود با مقدار \(C\) صفر و نقطۀ آغاز نامشخص، \(s\)، استفاده می کنید. متوجه شدید؟
چرا این قضیه درست کار می کند: ارتباط بین انتگرال گیری و مشتق گیری
توضیح بعدی از نسخۀ میانبر قضیۀ اساسی حسابان شامل ارتباط یین/یانگ (yin/yang relationship) بین مشتق گیری و انتگرال گیری می باشد. شکل 9-15 را بررسی کنید.

این شکل تابع \(f(x)=x^2+x\) و مشتق آن، \(f'(x)=2x+1\)، را نشان می دهد. با دقت به اعداد \(4\)، \(6\)، و \(8\) بر روی هر دو نمودار نگاه کنید. ارتباط بین \(4\)، \(6\)، و \(8\) بر روی نمودار \(f\) ـــ که مقادیر بالا رفتن بین نقاط متوالیِ بر روی این منحنی می باشند ـــ و \(4\)، \(6\)، و \(8\) بر روی نمودار \(f'\) ـــ که مساحت های ذوزنقه های زیر \(f'\) می باشند ـــ ارتباط صمیمیِ بین انتگرال گیری و مشتق گیری را نشان می دهند. شکل 9-15 از آن تصاویری است که به قول معروف برابر هزار کلمه می ارزند، این شکل جوهرۀ انتگرال گیری را در یک عکس آنی نشان می دهد. این شکل نشان می دهد چگونه نسخۀ میانبر قضیۀ اساسی حسابان درست کار می کند زیرا نشان می دهد که مساحت زیر \(f'(x)\) بین \(1\) و \(4\) برابر است با مجموع بالا رفتن بر روی \(f(x)\) بین \((1,2)\) و\((4,20)\)، به عبارت دیگر:
$$\int_1^4 f'(x)=f(4)-f(1)$$
توجه داشته باشید که من این دو تابع موجود در شکل 9-15 و معادلۀ بالا را \(f\) و \(f'\) نامیده ام تا روی این نکته تاکید کنم که \(2x+1\) مشتق \(x^2+x\) می باشد. من می توانستم به جای این کار به \(x^2+x\) به عنوان \(F\) و به \(2x+1\) به عنوان \(f\) اشاره کنم که در آن صورت روی این نکته تاکید می شد که \(x^2+x\) ضدمشتقی از \(2x+1\) می باشد. در آن صورت شما این معادلۀ مساحت بالا را در شکل استانداردش می نوشتید:
$$\int_1^4 f(x)dx=F(4)-F(1)$$
در هر دو صورت، معنا یکسان است. من از نسخۀ مشتق استفاده کردم تا اشاره کنم چگونه یافتن مساحت برابر با معکوس مشتق گیری می باشد. حرکت از سمت چپ به سمت راست در شکل 9-15 برابر با مشتق گیری می باشد: شیب های \(f\) با ارتفاع های \(f'\) متناظر می باشند. حرکت از سمت راست به چپ انتگرال گیری می باشد: مساحت های زیر \(f'\) با تغییر در ارتفاع بین دو نقطۀ موجود بر روی \(f\) متناظر می باشند.
اوکی، در اینجا چگونگی کارکرد آن را می بینید. تصور کنید در امتداد \(f\) از \((1,2)\) تا \((2,6)\) بالا می روید. هر نقطه در امتداد این مسیر دارای تندی (شیب) خاصی می باشد. این شیب (slope) به عنوان مختصات \(y\)، یا ارتفاع، بر روی نمودار \(f'\) ترسیم شده است. این واقعیت که \(f'\) از \((1,3)\) تا \((2,5)\) بالا می رود، به شما می گوید همینطور که بین \((1,2)\) و \((2,6)\) سفر می کنید، شیب \(f\) از \(3\) تا \(5\) بالا می رود. همۀ اینها از مبانی مشتق گیری پیروی می کنند.
اکنون، همینطور که در امتداد \(f\) از \((1,2)\) تا \((2,6)\) پیش می روید، این شیب به طور مداوم تغییر می کند. اما معلوم می شود از آنجا که به ازاء هر \(1\) واحدی که پیش می روید، \(4\) واحد بالا می روید، میانگین تمامی شیب های \(f\) بین \((1,2)\) و \((2,6)\) برابر با \(\frac{4}{1}\) یا \(4\) می باشد. از آنجا که هر کدام از این شیب ها، بر روی \(f'\) به عنوان مختصات \(y\) یا ارتفاع، ترسیم شده اند، نتیجه می شود که میانگین ارتفاع \(f'\) بین \((1,3)\) و \((2,5)\) نیز برابر با \(4\) می باشد. بنابراین، بین این دو نقطۀ داده شده، میانگین شیب بر روی \(f\) با میانگین ارتفاع بر روی \(f'\) برابر می باشند.
صبر کنید، شما تقریباً به هدف رسیده اید. شیب برابر با \(\frac{\text{rise}}{\text{run}}\) می باشد، بنابراین هنگامی که run برابر با \(1\) باشد، شیب برابر با rise می باشد. به عنوان مثال، از \((1,2)\) تا \((2,6)\) بر روی \(f\)، این منحنی \(4\) واحد بالا می رود و میانگین شیب بین آن نقاط نیز برابر با \(4\) می باشد. بنابراین، بین هر دو نقطه ای بر روی \(f\) که مختصات \(x\) آن \(1\) واحد با یکدیگر فرق داشته باشند، میانگین شیب برابر با rise می باشد.
مساحت یک ذوزنقه (trapezoid) مانند آنهایی که در سمت راست شکل 9-15 می بینید، برابر با عرض آن ضربدر میانگین ارتفاع آن می باشد. (این فرمول برای هر شکل مشابه دیگری که دارای انتهایی همانند یک مستطیل باشد، صدق می کند؛ بالای آن می تواند هر خط کج یا هر منحنی غیرمعمولی باشد که شما دوست داشته باشید.) بنابراین، از آنجا که عرض هر ذوزنقه برابر با \(1\) است، و از آنجا که هر چیزی ضربدر \(1\) برابر با خودش می شود، میانگین ارتفاع هر ذوزنقۀ زیر \(f'\) مساحت آن می باشد؛ به عنوان نمونه، مساحت ذوزنقۀ اول برابر با \(4\) و میانگین ارتفاع آن نیز برابر با \(4\) می باشد.
آیا برای فینال بزرگ آماده هستید؟ در اینجا کل این استدلال را به صورت خلاصه داریم. بر روی \(f\)، \(\text{rise}=\text{average slope}\)؛ وقتی از \(f\) به \(f'\) برویم، \(\text{average slope} = \text{average height}\)؛ بر روی \(f'\)، \(\text{average height} = \text{area}\). بنابراین، نتیجه می شود \(\text{rise} = \text{slope} = \text{height} = \text{area}\)، و بدین ترتیب، در نهایت، \(\text{rise}=\text{area}\). و این چیزی است که نسخۀ دوم قضیۀ اساسی حسابان بیان می دارد:
$$f(b)-f(a)=\int_a^b f'(x)dx \\
\text{rise} = \text{area}$$
این مفاهیم به طرز اجتناب ناپذیری دشوار می باشند. شما ممکن است مجبور شوید دو یا سه مرتبه آن را بخوانید تا درعمق آن فرو بروید.
توجه داشته باشید که اگر هر تابع دیگری از شکل \(x^2+x+C\) را به جای \(x^2 + x\) استفاده کنید، در ارتباط بین شیب و مساحت هیچ تفاوتی ایجاد نمی کند. هر سهمی مانند \(x^2+x+10\) یا \(x^2+x-5\) دقیقاً شکل یکسانی با \(x^2+x\) دارد؛ آن صرفاً به صورت عمودی به سمت بالا یا پایین می لغزد. هر سهمی مشابه دیگری، دقیقاً به شیوۀ یکسانی با سهمی موجود در شکل 9-15، بین \(x=1\) و \(x=4\) بالا می رود. از \(1\) تا \(2\) ، این سهمی ها \(1\) واحد رو به جلو و \(4\) واحد رو به بالا می روند. از \(2\) تا \(3\)، آنها \(1\) رو به جلو و \(6\) رو به بالا می روند، وبه همین ترتیب. به همین دلیل هم است که از هر ضدمشتقی می توانید برای یافتن مساحت استفاده کنید. مجموع مساحت زیر \(f'\) بین \(1\) و \(4\)، یعنی \(18\)، با مجموع بالا رفتن بر روی هر کدام از این سهمی ها از \(1\) تا \(4\)، یعنی \(4+6+8=18\) برابر می باشد.
با پذیرش این ریسک که ممکن است آب در هاون بکوبم، توضیحات سوم مربوط به قضیۀ اساسی حسابان را برای شما می آورم. شما ممکن است آن را بر دو توضیح اول ترجیح بدهید، زیرا کمتر انتزاعی می باشد ـــ آن براساس مفاهیم ساده و مبتنی بر فهم عمومی، که ما در زندگی روزمره با آنها برخورد داریم می باشد. این توضیح با توضیح قبلی چیزهای مشترک بسیاری دارد، اما مفاهیم ارائه شده در آن از زاویه ای دیگر مورد بررسی قرار گرفته اند.
چرا این قضیه درست کار می کند: ارتباط با آمار
اجازه ندهید عنوان این بخش منجر شود شما مطالعۀ آن را به زمان دیگری موکول کنید. من درک می کنم که بسیاری از خوانندگان این کتاب حسابان ممکن است هنوز آمار (statistics) را مطالعه نکرده باشند. نگران نباشید؛ ارتباط با آماری که در زیر توضیح داده ام شامل یک چیز خیلی ساده است که در دوره های آمار پوشش داده شده است، اما برای درک این مفهوم به هیچ وجه نیازی ندارید که آمار بدانید. این مفهوم ساده ارتباط بین یک نمودار توزیع فراوانی (frequency distribution graph) و یک نمودار توزیع فراوانی تجمعی (cumulative frequency distribution graph) می باشد (شما ممکن است در یک روزنامه یا مجله با چنین نمودارهایی روبرو شده باشید). شکل 10-15 را در نظر بگیرید.

نمودار بالایی در این شکل یک نمودار ستونی (هیستوگرام/histogram) از سود سالانه از شرکت Widgets-R-Us را از 1 ژانویۀ 2001 تا 31 دسامبر 2013 نشان می دهد. به عنوان مثال، مستطیل نشان گذاری شده با \(07\) نشان می دهد که سود این شرکت برای 2007 برابر با \($2,000,000\) بوده است (سال 2007 بهترین سال آنها در طول \(\text{2001-2013}\) می باشد).
نمودار پایینی در این شکل یک نمودار ستونی (هیستوگرام) توزیع فراوانی تجمعی برای همان داده ها می باشد که در نمودار بالایی مورد استفاده قرار گرفته اند. تفاوت به سادگی در اینست که در نمودار تجمعی، ارتفاع هر ستون، سود بدست آمده از \(\text{1/1/2001}\) را نشان می دهد. به عنوان مثال، به ستون \(02\) در نمودار پایین و مستطیل های \(01\) و \(02\) در نمودار بالا نگاه کنید. شما می توانید ببینید که ستون \(02\) یک مستطیل \(02\) را نشان می دهد که بر روی یک مستطیل \(01\) نشسته است که منجر می شود ستون \(02\) دارای ارتفاعی برابر با مجموع سودهای \(01\) و \(02\) باشد. متوجه شدید؟ همینطور که به سمت راست نمودار تجمعی پیش می روید، ارتفاع هر ستون متوالی به سادگی به میزان سودهای بدست آمده در سالهای مجزای متناظر نمایش داده شده در نمودار بالایی، رشد می کند.
اوکی. پس ارتباط حسابان آن را در اینجا می بینید. (شکیبایی کنید؛ اندکی طول می کشد تا گام به گام در این فرآیندها پیش برویم.) به مستطیل بالایی در ستون \(08\) بر روی نمودار تجمعی بنگرید (بیایید برای خلاصه سازی این نمودار را \(C\) بنامیم). در این مرحله، بر روی \(C\) شما \(1\) سال رو به جلو می روید (run)، و معادل \($1,250,000\) رو به بالا می روید (up)، سود \(08\) را بر روی نمودار توزیع می بینید (به نمودار بالا با \(F\) اشاره می کنیم). ما می دانیم که شیب برابر است با \(\frac{\text{rise}}{\text{run}}\)، بنابراین از آنجا که run برابر با \(1\) می باشد، شیب برابر با \(\frac{1,250,000}{1}\) یا فقط \(1,250,000\) می باشد، که مسلماً همان rise است. بدین ترتیب، شیب بر روی \(C\) (در \(08\) یا هر سال دیگر) می تواند به عنوان ارتفاع بر روی \(F\) برای سال متناظرش، خوانده شود. (مطمئن شوید که چگونگی کارکرد آن را بدانید.) از آنجا که ارتفاع ها (یا مقادیر تابع) بر روی \(F\) شیب های \(C\) می باشند، \(F\) مشتق \(C\) می باشد. به طور خلاصه، \(F\)، مشتق، در مورد شیب \(C\) به ما می گوید.
مفهوم بعدی اینست، از آنجا که \(F\) مشتقی از \(C\) می باشد، بنابه تعریف، \(C\) ضدمشتقی از \(F\) است (به عنوان مثال، \(C\) ممکن است برابر با \(5x^3\) و \(F\) برابر با \(15x^2\) باشد). حالا، \(C\)، ضدمشتق \(F\)، در مورد \(F\) به ما چه می گوید؟ تصور کنید، یک خط عمودی از چپ به راست بر روی \(F\) بکشید. همینطور که در \(F\) از روی این مستطیل ها ـــ سال به سال ـــ عبور می کنید مجموع کل مساحتی که از روی آن عبور می کنید در امتداد \(C\) به صورت بالا رفتن نشان داده می شود.
به مستطیل های \(01\) تا \(08\) بر روی \(F\) بنگرید. شما می توانید آن مستطیل های یکسان را که به صورت پلکانی در امتداد \(C\) بالا می روند را ببینید (مستطیل هایی را که با \(A\)، \(B\)، \(C\) و \(etc.\) نامگذاری شده اند را بر روی هر دو نمودار ببینید). همینطور که بر روی این شکل پلکانی بالا می روید، ارتفاع های مستطیل های \(F\) بر روی \(C\) با یکدیگر جمع می شوند. و من نشان داده ام که چگونه مستطیل های یکسان \(01\) تا \(08\) که در امتداد بالای پلکانی \(C\) قرار گرفته اند، نیز می توانند در سال \(08\) بر روی \(C\) به شکل یک پشتۀ عمودی دیده شوند. من نمودار تجمعی را به این شیوه ترسیم کرده ام تا حتی بیش از پیش نمایان شود که ارتفاع مستطیل ها با یکدیگر جمع می شوند. (توجه: بیشتر نمودارهای ستونی تجمعی اینگونه ترسیم نمی شوند.)
هر مستطیل بر روی \(F\) دارای پایه ای از \(1\) سال می باشد، بنابراین، از آنجا که \(\text{area} = \text{base} \times \text{height}\)، مساحت هر مستطیل برابر با ارتفاع آن می باشد. بنابراین، همینطور که این مستطیل ها را در \(C\) بر روی هم انباشته می کنید، مساحت های آن مستطیل های موجود در \(F\) را با یکدیگر جمع می کنید. به عنوان مثال، ارتفاع مستطیل های انباشته شده از \(01\) تا \(08\) بر روی \(F\) \(($ 8.5 \text{ million})\) برابر با مجموع مساحت مستطیل های \(01\) تا \(08\) بر روی \(F\) می باشد. و بنابراین، ارتفاع یا مقادیر تابع در \(C\) ـــ که ضدمشتق \(F\) می باشد ـــ مساحت زیر لبۀ بالای \(F\) را به شما می دهد. این چگونگی کارکرد انتگرال گیری می باشد.
اوکی، ما تقریباً کار را انجام دادیم. حالا به سراغ این مسأله می رویم که چگونه این دو نمودار نسخۀ میانبر قضیۀ اساسی حسابان و ارتباط بین مشتق گیری و انتگرال گیری را توصیف می کنند. به مستطیل های \(06\) تا \(12\) بر روی \(F\) بنگرید (که دارای حاشیۀ پررنگ می باشند). شما می توانید مستطیل های یکسانی با آنها را در بخش پررنگ شده در ستون \(12\) از \(C\) ببینید. ارتفاع آن پشتۀ پررنگ شده، که مجموع سود بدست آمده در طول آن \(7\) سال را نشان می دهد، \($7.75 \text{ million}\)، برابر با مجموع مساحت این \(7\) مستطیل بر روی \(F\) می باشد. و برای بدست آوردن ارتفاع این پشته بر روی \(C\)، شما به سادگی ارتفاع لبۀ پایینی این پشتۀ را از ارتفاع لبۀ بالایی آن تفریق می کنید. این در واقع تمامی چیزی است که نسخۀ میانبر قضیۀ اساسی حسابان بیان می دارد: مساحت زیر هر بخشی از هر تابعی (مانند \(F\)) با تغییر در ارتفاع ضدمشتق آن تابع (مانند \(C\)) بدست می آید.
به طور خلاصه (به نگاه کردن به آن مستطیل های دارای حاشیۀ پررنگ بر روی هر دو نمودار ادامه دهید)، شیب های مستطیل ها بر روی \(C\) به عنوان ارتفاع ها در \(F\) نمایان می شوند. این مشتق گیری است. در جهت معکوس، شما انتگرال گیری را می بینید: تغییر در ارتفاع ها بر روی \(C\) مساحت زیر \(F\) را نشان می دهد. مشتق گیری و انتگرال گیری دو روی یک سکه هستند.
توجه: ریاضیدانان محض ممکن است به این توضیح از قضیۀ اساسی حسابان اعتراض داشته باشند زیرا شامل نمودارهای گسسته می باشد (به عنوان مثال، این حقیقت که نمودار ستونی توزیع فراوانی تجمعی در شکل 10-15 در افزایش هر یک سال بالا می رود)، در حالیکه حسابان مطالعۀ نمودارهایی می باشد که به صورت نرم و مداوم تغییر می کنند (نسخۀ حسابانی از نمودار ستونی توزیع فراوانی تجمعی می تواند یک منحنی نرم باشد که مجموع رشد سود را در هر میلی ثانیه نشان می دهد ـــ در واقع، به لحاظ نظری، در هر کسر بی نهایت کوچک از ثانیه). اوکی ـــ به اعتراض اشاره شد ـــ اما واقعیت اینست که توضیحاتی که در اینجا ارائه شد به درستی نشان می دهند که چگونه انتگرال گیری و مشتق گیری با یکدیگر مرتبطند و به درستی نشان می دهند که نسخۀ میانبر قضیۀ اساسی حسابان چگونه کار می کند. تمام کاری که برای تبدیل شکل 10-15 و توضیحات همراه آن به حسابان استاندارد باید انجام بدهید اینست که همه چیز را به حد ببرید، بازۀ سود را کوتاهتر و کوتاهتر و باز هم کوتاهتر کنید: از یک سال به یک ماه به یک روز و ... . با حد، نمودارهای گسستۀ موجود در شکل 10-15 به نمودارهای نرم حسابانی تبدیل می شوند. اما مفاهیم تغییر نمی کند. مفاهیم دقیقاً همانهایی خواهند بود که در اینجا توضیح داده شدند.
خوب، به همین سادگی ـــ توضیحات واقعی برای اینکه چرا نسخۀ میانبر قضیۀ اساسی حسابان به درستی کار می کند و چرا یافتن مساحت معکوس مشتق گیری می باشد. اگر فقط نیمی از آنچه را که نوشتم درک کردید، از بیشتر دانش آموزان حسابان جلوترید. خبر خوب اینست که به احتمال زیاد از این چیزهای تئوری از شما امتحانی گرفته نمی شود. حالا بیایید دوباره به کرۀ زمین باز گردیم.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: