همانطور که در فصل 14 گفتم، انتگرال گیری در واقع صرفاً جمع زدن تکه های کوچک ـــ در حقیقت تکه های بی نهایت کوچک ـــ از چیزی برای رسیدن به کل یک چیز است.





بدین ترتیب، انتگرال
$$\int_{5 sec.}^{20 sec.} \text{little piece of distance}$$
به شما می گوید، تمامی تکه های کوچک از مسافت پیموده شده در طول \(15\) ثانیه در بازۀ \(5\) تا \(20\) ثانیه را با یکدیگر جمع بزنید تا مجموع مسافت پیموده شده در طول این بازه را بدست آورید.

در تمامی مسأله ها، این تکۀ کوچک بعد از نماد انتگرال گیری همواره عبارتی در \(x\) (یا متغیری دیگر) می باشد. به عنوان مثال، در انتگرال بالا، این تکۀ کوچک از مسافت می تواند فرضاً با \(x^2 dx\) مشخص شود، سپس انتگرال معین آن
$$\int_5^{20} x^2 dx$$
مجموع مسافت پیموده شده را به شما می دهد. از آنجا که شما هم اکنون در محاسبۀ انتگرال هایی مانند انتگرال بالا، یک خبره هستید، این دیگر برای شما صورت مسأله نیست؛ چالش اصلی شما در این فصل به سادگی اینست که به عبارت جبری که آن تکۀ کوچک برای جمع زدن را می دهد، برسید. اما پیش از آنکه مسأله های جمع زدن را آغاز کنیم، می خواهم چندین موضوع انتگرال گیری دیگری را پوشش بدهم: مقدار میانی (mean value) و مقدار میانگین (average value).

قضیۀ مقدار میانی برای انتگرال ها و مقدار میانگین

بهترین روش برای درک قضیۀ مقدار میانی برای انتگرال ها استفاده از یک نمودار است ـــ به شکل 1-17 بنگرید:


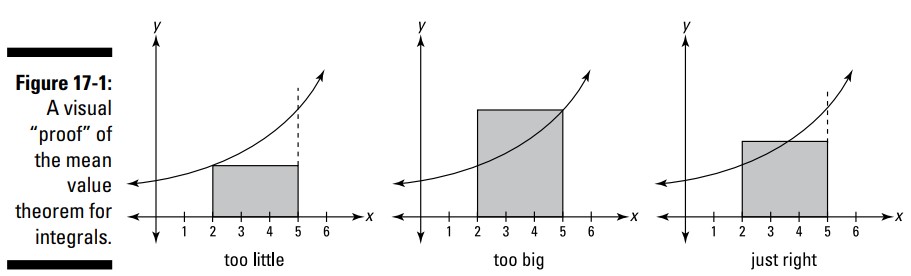
نمودار سمت چپ در شکل 1-17 مستطیلی را نشان می دهد که مساحت آن به وضوح کمتر از مساحت زیر منحنی بین \(2\) و \(5\) می باشد. این مستطیل دارای ارتفاعی برابر با پایننترین نقطه بر روی این منحنی در بازۀ \(2\) تا \(5\) می باشد. نمودار میانی مستطیلی را نشان می دهد که ارتفاع آن برابر با بالاترین نقطه بر روی این منحنی می باشد. مساحت آن بوضوح بزرگتر از مساحت زیر منحنی می باشد. تا اینجا شما فکر می کنید، آیا مستطیلی نداریم که بلندتر از این مستطیل کوتاه و کوتاهتر از این مستطیل بلند باشد که مساحت آن با مساحت زیر این منحنی برابر باشد؟ البته که داریم. و این مستطیل به طور واضح در جایی از این بازه این منحنی را قطع می کند. این به اصطلاح "مستطیل مقدار میانی" (mean value rectangle) که در سمت راست نشان داده شده است، در واقع قضیۀ مقدار میانی برای انتگرال ها (mean value theorem for integrals) را خلاصه می کند. این صرفاً مبتنی بر خرد عمومی است. اما در ادامه بیان ریاضی آن را هم داریم.


در واقع این قضیه صرفاً وجود مستطیل نقطۀ میانی (mean value rectangle) را تضمین می کند. (توجه داشته باشید که تنها یک مستطیل مقدار میانی می تواند وجود داشته باشد، اما بالای آن گاهی بیش از یک بار از این تابع عبور می کند. بدین ترتیب، ممکن است بیش از یک مقدار \(c\) باشد که این قضیه را برآورده سازد.)

مساحت مستطیل نقطۀ میانی ـــ که با مساحت زیر منحنی برابر است ـــ برابر با طول ضربدر عرض می باشد، یا قاعده ضربدر ارتفاع. بنابراین، اگر مساحت آن، \(\int_a^b f(x)dx\)، را بر قاعدۀ آن، \((b-a)\)، تقسیم کنید به ارتفاع آن، \(f(c)\) می رسید. این ارتفاع مقدار میانگین (average value) این تابع در بازۀ مسأله می باشد.


در اینجا مثالی داریم. سرعت میانگین یک خودرو بین \(t=9\) ثانیه و \(t=16\) ثانیه که سرعت آن در واحد فوت بر ثانیه با تابع \(f(t)=30\sqrt{t}\) تعیین می شود، چقدر است؟ تعریف مقدار میانگین، پاسخ این مسأله را در یک مرحله به شما می دهد: سرعت میانگین برابر با \(\frac{1}{16-9} \int_9^{16} 30 \sqrt{t} dt\) است. این انتگرال را ارزیابی کنید و کار تمام است. (به همین سادگی، بنابراین فرآیند دو مرحله ایِ زیر تاحدی غیرضروری است. با این حال، منطق قرار گرفته در زیر مفهوم مقدار میانگین را نشان می دهد.)

1. مساحت زیر این منحنی بین \(9\) و \(16\) را تعیین کنید. $$\int_9^{16} 30 \sqrt{t}dt \\
   =30 \biggl[ \frac{2}{3}t^{\frac{3}{2}} \biggr]_9^{16} \\
   = 30 \biggl( \frac{128}{3}-\frac{54}{3} \biggr) \\
   =740$$
   در ضمن این مساحت، مجموع مسافت پیموده شده در طول بازۀ \(9\) تا \(16\) ثانیه می باشد، یعنی \(740\) فوت. آیا می دانید چرا اینگونه است؟ مستطیل مقدار میانی را برای این مسأله در نظر بگیرید. ارتفاع آن یک سرعت است (زیرا مقادیر تابع، یا ارتفاع ها، سرعت ها می باشند) و قاعدۀ آن مقداری از زمان است، بنابراین مساحت آن برابر با سرعت ضربدر زمان که برابر با مسافت می شود، می باشد. از سوی دیگر، بیاد بیاورید که مشتق موقعیت برابر با سرعت سیر (velocity) می باشد (فصل 12 را ببینید). بنابراین، ضدمشتق سرعت سیر ـــ چیزی که درست در همین مرحله انجام دادم ـــ برابر با موقعیت است، و تغییر موقعیت از \(9\) تا \(16\) ثانیه، مجموع مسافت پیموده شده را به شما می دهد.
   
   
2. این مساحت، مجموع مسافت، را بر بازۀ زمان \(9\) تا \(16\)، یعنی \(7\)، تقسیم کنید. $$\text{Average speed} = \frac{\text{total distance}}{\text{total time}} = \frac{740 \text{ feet}}{7 \text{ seconds}} \approx 105.7 \text{ feet per second}
   $$
   تعریف مقدار میانگین به شما می گوید، مجموع مساحت را در \(\frac{1}{b-a}\)، که در این مسأله برابر با \(\frac{1}{16-9}=\frac{1}{7}\)، ضرب کنید. اما از آنجا که تقسیم بر \(7\) با ضرب کردن در \(\frac{1}{7}\) یکسان است، شما مانند آنچیزی که من در این مرحله انجام داده ام، می توانید تقسیم را انجام دهید. اگر به این مسأله به لحاظ تقسیم فکر کنید، معنادارتر می شود: مساحت برابر با قاعده ضربدر ارتفاع می باشد، بنابراین ارتفاع مستطیل مقدار میانی برابر با مساحت آن تقسیم بر قاعده اش می باشد.