خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
پاسخنامه کار با اعداد

در اینجا پاسخ 24 تمرینی را داریم که به موضوعات مختلف در ارتباط با کار با اعداد می پردازند. برای مشاهدۀ خود سوالات اینجا کلیک کنید.


-
-
\(9\) رقم یکان است
-
\(5\) رقم دهگان است
-
\(3\) رقم صدگان است
-
\(7\) رقم هزارگان است
-
\(9\) رقم یکان است
-
\(2,000+100+30+6=2,136\)

-
\(0+3,000+800+0+9=3,809\)
اولین \(0\) صفر پیشرو می باشد و دومین \(0\) جایبان است.

-
\(0+400,000+50,000+0+900+0+0=0,450,900\)
اولین \(0\) صفر پیشرو می باشد و بقیۀ \(0\)ها، جایبان هستند.

-
-
\(29 \to 30\)
رقم یکان \(9\) می باشد، بنابراین به بالا گرد می شود.
-
\(43 \to 40\)
رقم یکان \(3\) می باشد، بنابراین به پایین گرد می شود.
-
\(75 \to 80\)
رقم یکان \(5\) می باشد، پس به سمت بالا گرد می شود.
-
\(95 \to 100\)
رقم یکان \(5\) می باشد، پس به سمت بالا گرد می شود.
-
\(29 \to 30\)
-
-
\(1\underline{64} \to 1\underline{60}\)
رقم یکان برابر با \(4\) است، پس به سمت پایین گرد می شود.
-
\(7\underline{65} \to 7\underline{70}\)
رقم یکان \(5\) است، پس به سمت بالا گرد می شود.
-
\(1,9\underline{89} \to 1,9\underline{90}\)
رقم یکان \(9\) است، پس به سمت بالا گرد می شود.
-
\(9,999,9\underline{95} \to 10,000,0\underline{00}\)
رقم یکان \(5\) است، پس به سمت بلا گرد می شود.
-
\(1\underline{64} \to 1\underline{60}\)
-
بر روی ارقام صدگان و دهگان تمرکز کنید تا به نزدیکترین صد گرد کنید.
-
\(\underline{43}9 \to \underline{40}0\)
رقم دهگان \(3\) است، پس به سمت پایین گرد می شود.
-
\(\underline{56}2 \to \underline{60}0\)
رفم دهگان \(6\) است، پس به سمت بالا گرد می شود.
-
\(2,\underline{95}0 \to 3,\underline{00}0\)
رقم دهگان \(5\) است، پس به سمت بالا گرد می شود.
-
\(109,\underline{97}4 \to 110,\underline{00}0\)
رقم دهگان \(7\) است، پس به سمت بالا گرد می شود.
-
\(\underline{43}9 \to \underline{40}0\)
-
برای گرد کردن به نزدیکترین هزار، بر روی ارقام هزارگان و صدگان تمرکز کنید.
-
\(\underline{5,2}80 \to \underline{5,0}00\)
رقم صدگان \(2\) است، پس به سمت پایین گرد می شود.
-
\(7\underline{7,7}77 \to 7\underline{8,0}00\)
رقم صدگان \(7\) است، پس به سمت بالا گرد می شود.
-
\(1,23\underline{4,5}67 \to 1,23\underline{5,0}00\)
رقم صدگان \(5\) است، پس به سمت بالا گرد می شود.
-
\(1,89\underline{9,9}99 \to 1,90\underline{0,0}00\)
رقم صدگان \(9\) است، پس به سمت بالا گرد می شود.
-
\(\underline{5,2}80 \to \underline{5,0}00\)
-
-
\(4+7=11\)
عبارت \(4 + 7\) بدین معناست که در \(4\) آغاز کنید، و \(7\) واحد بالا بروید، که شما به به \(11\) می رساند.
-
\(9+8=17\)
در \(9\) آغاز کنید، \(8\) واحد بالا بروید، که شما را به \(17\) می رساند.
-
\(12+0=12\)
در \(12\) آغاز کنید، \(0\) واحد بالا بروید، که شما را به \(12\) می رساند.
-
\(4+6+1+5=16\)
در \(4\) آغاز کنید، \(6\) واحد بالا بروید، \(1\) واحد بالا بروید، \(5\) واحد بالا بروید، که شما را به \(16\) می رساند.
-
\(4+7=11\)
-
-
\(10-6=4\)
عبارت \(10-6\) بدین معناست که در \(10\) آغاز کنید، \(6\) واحد پایین بروید، که شما را به \(4\) می رساند.
-
\(14-9=5\)
در \(14\) آغاز کنید، \(9\) واحد پایین بروید، که شما را به \(5\) می رساند.
-
\(18-18=0\)
در \(18\) آغاز کنید، \(18\) واحد پایین بروید، که شما را به \(0\) می رساند.
-
\(9-3+7-2+1=12\)
در \(9\) آغاز کنید، \(3\) واحد پایین بروید، \(7\) واحد بالا بروید، \(2\) واحد پایین بروید، \(1\) واحد بالا بروید، که شما را به \(12\) می رساند.
-
\(10-6=4\)
-
-
\(2 \cdot 7=14\)
در \(0\) آغاز کنید، در مجموع \(7\) بار دوتا دوتا شمارش کنید، که شما را به \(14\) می رساند.
-
\(7 \cdot 2=14\)
در \(0\) آغاز کنید، روی هم رفته \(2\) بار، شمارش \(7\)تایی را انجام دهید، که شما را به \(14\) می رساند.
-
\(4 \cdot 3=12\)
در \(0\) آغاز کنید، شمارش \(4\)تایی را \(3\)بار انجام دهید، که شما را به \(12\) می رساند.
-
\(6 \cdot 1=6\)
در \(0\) آغاز کنید، شمارش \(6\)تایی را \(1\)مرتبه انجام دهید، که شما را به \(6\) می رساند.
-
\(6 \cdot 0=0\)
در \(0\) آغاز کنید، شمارش \(6\)تایی را \(0\)مرتبه انجام دهید، که شما را به \(0\) می رساند.
-
\(0 \cdot 10=0\)
در \(0\) آغاز کنید، شمارش \(0\) تایی را \(10\)بار انجام دهید، که شما را به \(0\) می رساند.
-
\(2 \cdot 7=14\)
-
-
\(8 \div 2=4\)
یک پاره خط از خط اعداد را از \(0\) تا \(8\) جدا کنید. اکنون این پاره خط را به صورت مساوی به دو تکه تقسیم کنید. هر کدام از این تکه ها دارای طول \(4\) می باشد، پس این پاسخ مسأله است.
-
\(15 \div 5=3\)
یک پاره خط از خط اعداد را از \(0\) تا \(15\) جدا کنید. اکنون این پاره خط را به صورت مساوی به پنج تکه تقسیم کنید. هر کدام از این تکه ها دارای طول \(3\) می باشد، پس این پاسخ مسأله است.
-
\(18 \div 3=6\)
یک پاره خط از خط اعداد را از \(0\) تا \(18\) جدا کنید. اکنون این پاره خط را به صورت مساوی به سه تکه تقسیم کنید. هر کدام از این تکه ها دارای طول \(6\) می باشد، پس این پاسخ مسأله است.
-
\(10 \div 10=1\)
یک پاره خط از خط اعداد را از \(0\) تا \(10\) جدا کنید. اکنون این پاره خط را به صورت مساوی به ده تکه تقسیم کنید. هر کدام از این تکه ها دارای طول \(1\) می باشد.
-
\(7 \div 1=7\)
یک پاره خط از خط اعداد را از \(0\) تا \(7\) جدا کنید. اکنون این پاره خط را به صورت مساوی به یک تکه تقسیم کنید. (در واقع هیچ تقسیمی صورت نمی پذیرد). این تکه هنوز هم دارای طول \(7\) خواهد بود.
-
\(0 \div 2=0\)
یک پاره خط از خط اعداد را از \(0\) تا \(0\) جدا کنید. طول این پاره خط \(0\) می باشد، بنابراین نمی توانید آن را کوچکتر کنید. این به شما نشان می دهد که \(0\) تقسیم بر هر عددی برابر با \(0\) خواهد بود.
-
\(8 \div 2=4\)
-
\(252\)
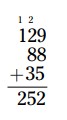
-
\(3,189\)
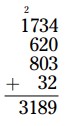
-
\(362\)
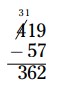
-
\(39,238\)
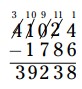
-
\(3,150\)
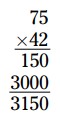
-
\(11,424\)
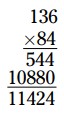
-
\(699,840\)

-
\(6,835,504\)
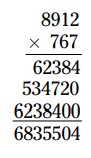
-
\(247\)
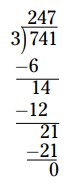
-
\(649\)
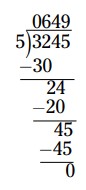
-
\(11,423 \text{ r } 6\)
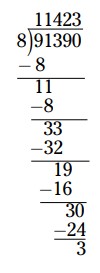
-
\(88,060 \text{ r } 1\)
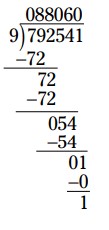
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: