مختصات دکارتی و نمودار خط

تمرینات این قسمت در ارتباط با این موضوعات می باشند: ترسیم نقاط بر روی گراف دکارتی، مختصات دکارتی نقاط، ترسیم نمودار خط. برای مشاهدۀ پاسخنامه اینجا کلیک کنید.

نقاط زیر را بر روی گراف دکارتی (Cartesian graph) نمایش دهید.
1. \(M = (5, 6)\)
2. \(N = (–6, –2)\)
3. \(O = (0, 0)\)
4. \(P = (–1, 2)\)
5. \(Q = (3, 0)\)
6. \(R = (0, 2)\)
مختصات دکارتی (Cartesian coordinates) هر کدام از نقاط \(S\) تا \(X\) را بنویسید.
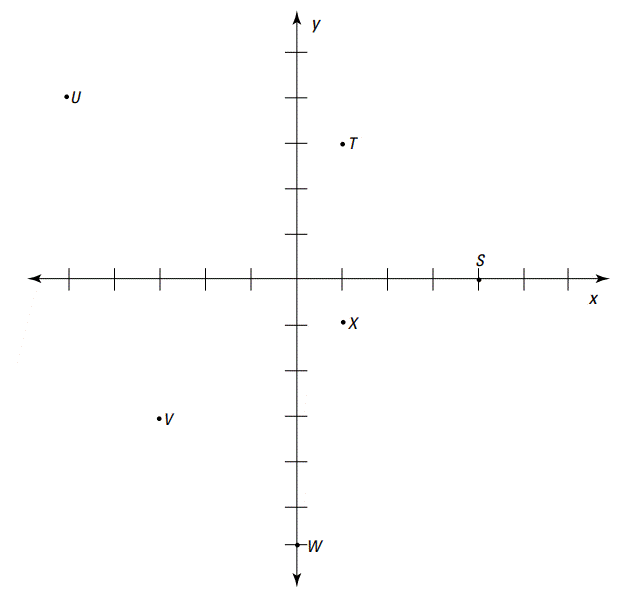
نمودار \(y=x-1\) را ترسیم کنید.
1. یک جدول ورودی-خروجی (input-output table) برای تابع \(y=x-1\) به ازاء مقادیر ورودی \(0,1,2,3,4\) بسازید.
2. از این جدول استفاده کنید تا مختصات دکارتی پنج نقطه بر روی این تابع را بنویسید.
3. این پنج نقطه را بر روی نمودار رسم کنید تا با استفاده از آنها نمودار تابع \(y=x-1\) را به عنوان نمودار یک خط ترسیم کنید.
نمودار \(y=2x\) را ترسیم کنید.
1. یک جدول ورودی-خروجی برای تابع \(y=2x\) به ازاء مقادیر ورودی \(0,1,2,3,4\) بسازید. (توجه داشته باشید که \(2x\) به معنای \(2 \cdot x\) می باشد.)
2. از این جدول استفاده کنید تا مختصات دکارتی پنج نقطه بر روی این تابع را بنویسید.
3. این پنج نقطه را بر روی نمودار قرار دهید تا با استفاده از آنها تابع \(y=2x\) را به عنوان نمودار یک خط ترسیم کنید.
نمودار \(y=3x-5\) را ترسیم کنید.
1. یک جدول ورودی-خروجی برای تابع \(y=3x-5\) به ازاء مقادیر ورودی \(0,1,2,3,4\) بسازید.
2. از این جدول استفاده کنید تا مختصات دکارتی پنج نقطه بر روی این تابع را بنویسید.
3. این پنج نقطه را بر روی نمودار قرار دهید تا با استفاده از آنها تابع \(y=3x-5\) را به عنوان نمودار یک خط ترسیم کنید.
نمودار \(y=\frac{x}{2} + 3\) را ترسیم کنید.
1. یک جدول ورودی-خروجی برای تابع \(y=\frac{x}{2} + 3\) به ازاء مقادیر ورودی \(-2,0,2,4\) بسازید.
2. از این جدول استفاده کنید تا مختصات دکارتی چهار نقطه بر روی این تابع را بنویسید.
3. این چهار نقطه را بر روی نمودار قرار دهید تا با استفاده از آنها تابع \(y=\frac{x}{2} + 3\) را به عنوان نمودار یک خط ترسیم کنید.

آموزش قبلی صفحۀ اصلی دوره آموزش بعدی

با معرفی سایت خوش آموز به دوستان و همکلاسی هایتان از ما حمایت کنید.

لیست دوره های آموزش ریاضی در سایت خوش آموز

ریاضی درسی

برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.

مطالب مرتبط :

دیدگاه ها(0)

دیدگاه خود را ثبت کنید:

انتخاب تصویر پیوست

انتخاب تصویر ویرایش حذف

توجه! حداکثر حجم مجاز برای تصویر 500 کیلوبایت می باشد.

لطفا پیش از ارسال دیدگاه ، به نکات زیر توجه فرمایید :

- از نوشتن دیدگاه های غیر مرتبط با پست جدا خودداری کنید. دیدگاه ها و سوالات متفرقۀ خود را می توانید در تالارهای گفتمان خوش آموز مطرح نمایید.
- لطفاً دیدگاه های خود را با حروف فارسی تایپ کنید، دیدگاه های فینگیلیش تایید نمی شوند.
- قبل از ارسال دیدگاه حتما متن پست و نظرات سایر دوستان را بخوانید . نظرات اسپم و تکراری تایید نخواهند شد.
- نظر شما ممکن است بدون پاسخ تایید شوند که در این صورت باید منتظر پاسخ از سوی دیگر کاربران باشید .
- لطفا انتقادات و پیشنهادات و همچنین درخواست های خود را از طریق ایمیل khoshamoz[at].hotmail.com ارسال نمایید
- چرا آموزش های سایت خوش آموز در قالب فایل pdf به صورت یکجا ارائه نمی شوند؟
- چرا برخی پرسش های کاربران پاسخ داده نمی شوند؟