خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
توابع توانی (Power Functions)

یک تابع \(f(x)=x^a\)، که در آن \(a\) یک ثابت (constant) باشد، یک تابع توانی (power function) نامیده می شود. در اینجا چندین مورد مهم وجود دارد که باید در نظر بگیرید.


-
\(a=n\) ، یک عدد صحیح مثبت است.
نمودار \(f(x)=x^n\) برای \(n=1,2,3,4,5\)، در شکل \(\text{1.15}\) نشان داده شده است. این توابع برای تمامی مقادیر حقیقی \(x\) تعریف شده اند. توجه داشته باشید که، همینطور که توان \(n\) بزرگتر می شود، منحنی ها تمایل به مسطح شدن به سمت محور \(x\) در بازۀ \((-1,1)\)، و بالا رفتن با شیب تُندتر در \(|x| \gt 1\)، پیدا می کنند. هر منحنی از نقطۀ \((1,1)\) و از مبدأ مختصات عبور می کند. نمودار این توابع با توانهای زوج پیرامون محور \(y\) متقارن (symmetric) می باشند؛ آنهایی که توان فرد دارند، پیرامون مبدأ مختصات متقارن هستند. توابع دارای توان زوج (even-powered functions) در بازۀ \((-\infty,0]\) کاهش می یابند و در بازۀ \([0,\infty)\) افزایش می یابند؛ توابع دارای توان فرد در سرتاسر کل خط حقیقی \((-\infty,\infty)\) افزایش می یابند.
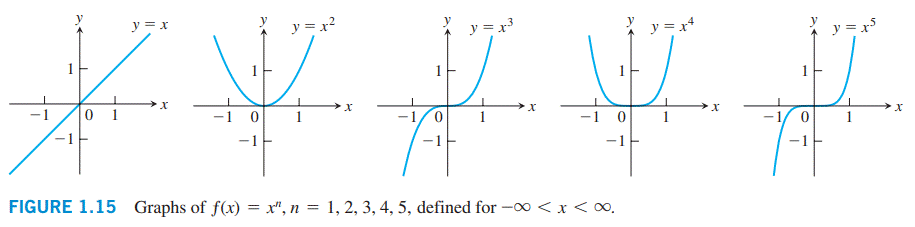
-
\(a=-1\) یا \(a=-2\)
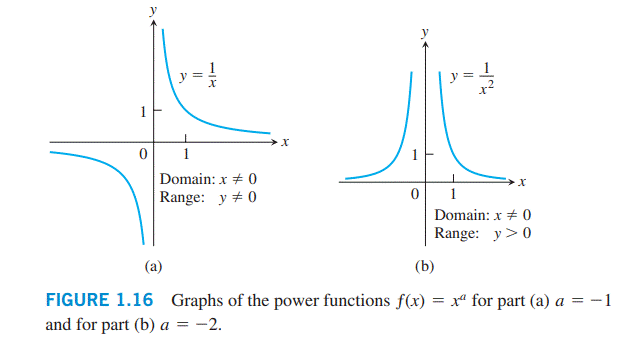
نمودارهای توابع \(f(x)=x^{-1}=\frac{1}{x}\) و \(g(x)=x^{-2}=\frac{1}{x^2}\) در شکل \(\text{1.16}\) نشان داده شده اند. هر دوی این توابع برای تمامی مقادیر \(x \ne 0\) تعریف می شوند (شما هرگز نمی توانید بر صفر تقسیم کنید). نمودار \(y=\frac{1}{x}\) هذلولی \(xy=1\) می باشد، که به محورهای مختصات دور از مبدأ نزدیک می شود. همچنین نمودار \(y=\frac{1}{x^2}\) به محورهای مختصات نزدیک می شود. نمودار تابع \(f\) پیرامون مبدأ مختصات، متقارن می باشد؛ \(f\) در بازه های \((-\infty,0)\) و \((0,\infty)\) کاهش می یابد (یعنی نزولی است). نمودار تابع \(g\) پیرامون محور \(y\) متقارن می باشد؛ \(g\) در بازۀ \((-\infty,0)\) افزایش می یابد (صعودی است) و در بازۀ \((0,\infty)\) کاهش می یابد (نزولی است).
-
\(a=\frac{1}{2},\frac{1}{3},\frac{3}{2},\frac{2}{3}\)
تابع \(f(x)=x^{\frac{1}{2}}=\sqrt{x}\) و \(g(x)=x^{\frac{1}{3}}=\sqrt[3]{x}\)، به ترتیب توابع ریشۀ دوم (square root) و ریشۀ سوم (cube root) می باشند. دامنۀ تابع ریشۀ دوم (جذر) برابر با \([0,\infty)\) می باشد، اما تابع ریشۀ سوم برای تمامی مقادیر حقیقی \(x\) تعریف می شود. نمودارهای آنها همراه با نمودارهای \(y=x^{\frac{3}{2}}\) و \(y=x^{\frac{2}{3}}\) در شکل \(\text{1.17}\) نشان داده شده اند. (بیاد بیاورید که \(x^{\frac{3}{2}}=(x^{\frac{1}{2}})^3\) و \(x^{\frac{2}{3}}=(x^{\frac{1}{3}})^2\) می باشند.)
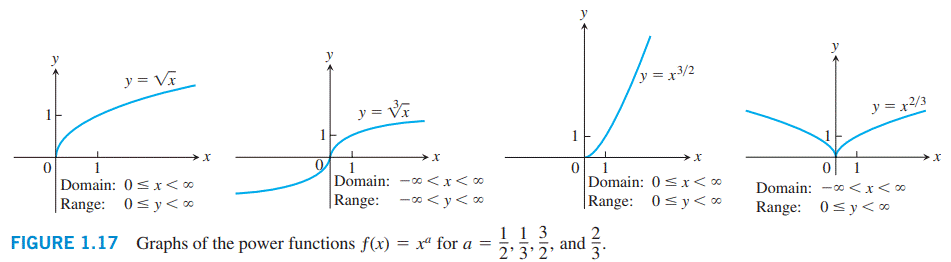
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: