خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
معادلۀ توابع درجه دوم (Graphs of Quadratic Functions)

در این آموزش با معادلۀ توابع درجه دوم و همینطور نمودار آن که سهمی (شلجمی) نام دارد آشنا می شوید. همچنین یک سری ویژگی های خاص و نکات کلیدی در ارتباط با آن وجود دارد که آن ها را نیز در می یابید.

نمودار یک تابع درجه دوم (quadratic function) یک سهمی (parabola) می باشد، نام دیگر سهمی، شلجمی می باشد. سهمی یا شلجمی اطلاعات ارزشمندی را دربارۀ تابع ارائه می دهد. در اینجا قصد داریم بخش های مختلف و ویژگی های یک سهمی را توضیح دهیم.
نکات کلیدی:
اصطلاحات کلیدی:
شکل کلی یک تابع درجه دوم اینگونه است: \(f(x) = ax^2 + bx + c\)
که در آن \(a\)، \(b\)، و \(c\) مقادیر ثابت (constants) می باشند، و \(a \ne 0\)
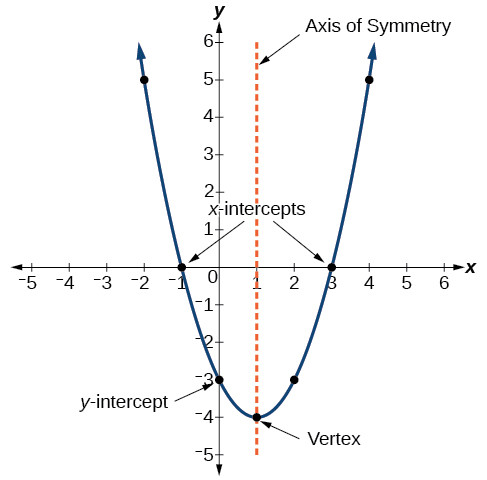
نمودار یک تابع درجه دوم، یک منحنی درجه دوم است که سهمی نامیده می شود. این شکل در تصویر زیر نشان داده شده است:
در نمودار توابع درجه دوم، علامت ضریب \(a\) بر روی اینکه نمودار آن تابع رو به پایین یا رو به بالا باز شود تاثیر گذار است. اگر \(a \lt 0\)، آن نمودار رو به پایین باز می شود (تبدیل به یک آدم منفی و غمگین می شود)، و اگر \(a \gt 0\)، نمودار آن تابع روی به بالا باز می شود (تبدیل به یک آدم مثبت و شاد می شود). تصاویر زیر این موضوع را نشان می دهند.
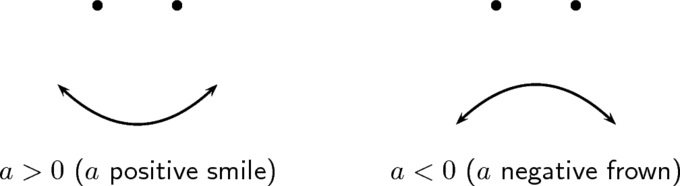

معادلۀ توابع درجه دوم (Graphs of Quadratic Functions)
نمودار یک تابع درجه دوم (quadratic function) یک سهمی (parabola) می باشد، نام دیگر سهمی، شلجمی می باشد. سهمی یا شلجمی اطلاعات ارزشمندی را دربارۀ تابع ارائه می دهد. در اینجا قصد داریم بخش های مختلف و ویژگی های یک سهمی را توضیح دهیم.
نکات کلیدی:
-
نمودار یک تابع درجه دوم، یک منحنی \(\text{U}\) شکل می باشد که به آن سهمی (شلجمی) گفته می شود.
-
علامت ضریب \(a\) در یک تابع درجه دوم، بر روی اینکه نمودار رو به پایین یا رو به بالا باز شود، تاثیر گذار است. اگر \(a \lt 0\) باشد، نمودار رو به پایین باز می شود و اگر \(a \gt 0\) باشد، نمودار آن رو به بالا باز می شود.
-
نقطۀ نهایی (extreme point) یک سهمی، رأس (vertex) نامیده می شود، نقطۀ نهایی ممکن است بالاترین نقطۀ نمودار یا پایینترین نقطۀ آن باشد، و خطی عمودی که از رأس می گذرد، محور تقارن (axis of symmetry) نامیده می شود.
-
طول از مبدأها (x-intercepts)، نقاطی هستند که در آن نقاط سهمی محور \(x\) را قطع می کند. اگر نموداری دارای طول از مبدأهایی باشد، آن نقاط نشان دهندۀ صفرها (zeros)، یا ریشه ها (roots) در آن تابع درجه دوم می باشند.
اصطلاحات کلیدی:
-
رأس (vertex): نقطه ای که در آن مسیر سهمی تغییر می کند، این نقطه با کوچکترین یا بزرگترین مقدار در آن تابع درجه دوم، متناظر است.
-
محور تقارن (axis of symmetry): یک خط عمودی که از رأس یک سهمی عبور می کند و سهمی در آن متقارن (symmetric) است.
-
صفرها (zeros): در یک تابع، مقادیری از \(x\) که در آنها \(y=0\) باشد، صفرها یا ریشه ها نامیده می شوند.
شکل کلی یک تابع درجه دوم اینگونه است: \(f(x) = ax^2 + bx + c\)
که در آن \(a\)، \(b\)، و \(c\) مقادیر ثابت (constants) می باشند، و \(a \ne 0\)
نمودار یک تابع درجه دوم، یک منحنی درجه دوم است که سهمی نامیده می شود. این شکل در تصویر زیر نشان داده شده است:
در نمودار توابع درجه دوم، علامت ضریب \(a\) بر روی اینکه نمودار آن تابع رو به پایین یا رو به بالا باز شود تاثیر گذار است. اگر \(a \lt 0\)، آن نمودار رو به پایین باز می شود (تبدیل به یک آدم منفی و غمگین می شود)، و اگر \(a \gt 0\)، نمودار آن تابع روی به بالا باز می شود (تبدیل به یک آدم مثبت و شاد می شود). تصاویر زیر این موضوع را نشان می دهند.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: