نویسنده : امیر انصاری

مفاهیم کلیدی

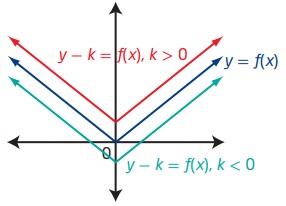
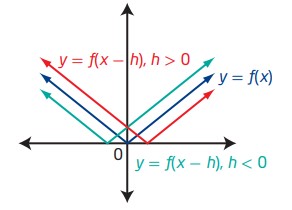
• انتقال ها (Translations) تبدیلاتی (transformations) هستند که تمامی نقاط نمودار یک تابع را به سمت بالا، پایین، چپ، و راست منتقل می کنند، بدون اینکه شکل یا جهت آن نمودار را تغییر دهند.
  
• جدول زیر انتقال های تابع \(y=f(x)\) را به صورت خلاصه وار نشان می دهد.
  
  برای بزرگنمایی تصویر روی آن کلیک کنید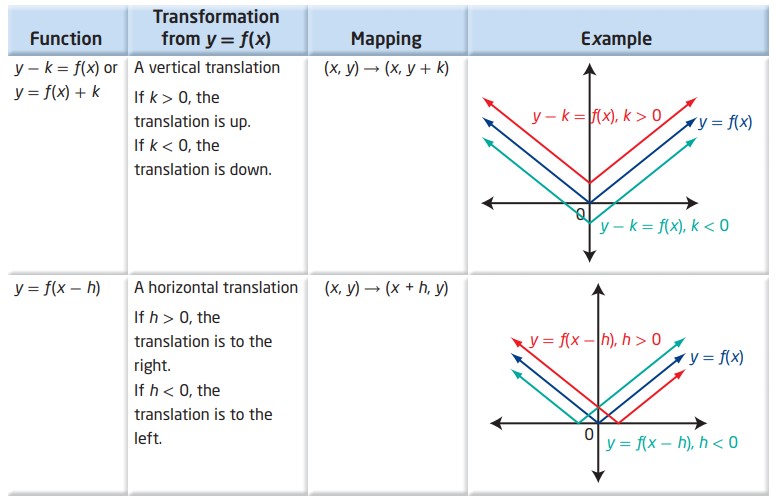
  ترجمۀ جدول

  تابع	تبدیل از \(y=f(x)\)	نگاشت	مثال
  \(y-k = f(x)\) یا \(y=f(x)+k\)	یک انتقال عمودی اگر \(k \gt 0\) انتقال رو به بالا است. اگر \(k \lt 0\) انتقال رو به پایین است.	\((x,y) \to (x, y+k)\)
  \(y = f(x-h)\)	یک انتقال افقی اگر \(h \gt 0\) انتقال به سمت راست است. اگر \(h \lt 0\) انتقال به سمت چپ است.	\((x,y) \to (x+h,y)\)

  
  
• ترسیم نمودار \(y-k = f(x-h)\) یا \(y=f(x-h)+k\) می تواند با منتقل کردن نقاط کلیدی بر روی نمودار تابع اصلی \(y=f(x)\) انجام شود.