نویسنده : امیر انصاری

پرسش

1. معادلۀ تابع \(y=g(x)\) را مشخص سازید.
   
2. دامنه و بُرد تابع تصویر (image function) چه می باشند؟
   
3. چگونه می توانید با استفاده از توصیف انتقال تابع \(y=x^2\)، دامنه و برد تابع تصویر را مشخص سازید؟
   

پاسخ

1. برای تعیین معادلۀ این تابع لازم است که مقادیر \(h\) و \(k\) را شناسایی کنیم. انتقال افقی \(4\) واحد به سمت چپ می باشد، پس \(h=-4\)، انتقال عمودی \(5\) واحد به سمت بالا می باشد، پس \(k=5\).
   $$
   h=-4, k =5 \\
   y-k=f(x-h) \\
   y-5=f(x-(-4)) \\
   y-5 = f(x+4) \\
   \text{ } \\
   y = x^2 \\
   y - 5 = (x+4)^2 \\
   \text{or} \\
   y=(x+4)^2 + 5
   $$
   
2. از آنجا که تابع تصویر، یک چندجمله ای می باشد، دامنۀ آن \((-\infty,\infty)\) است.
   این تابع یک چندجمله ای درجه دوم است که رأس آن در \((h,k)\) قرار دارد و جهت آن نیز رو به بالا است، پس بُرد آن \([5,\infty)\) می باشد.
   برای درک بهتر دامنه و برد این تابع می توانید نمودار آن را نیز بررسی کنید.
   
   برای بزرگنمایی تصویر روی آن کلیک کنید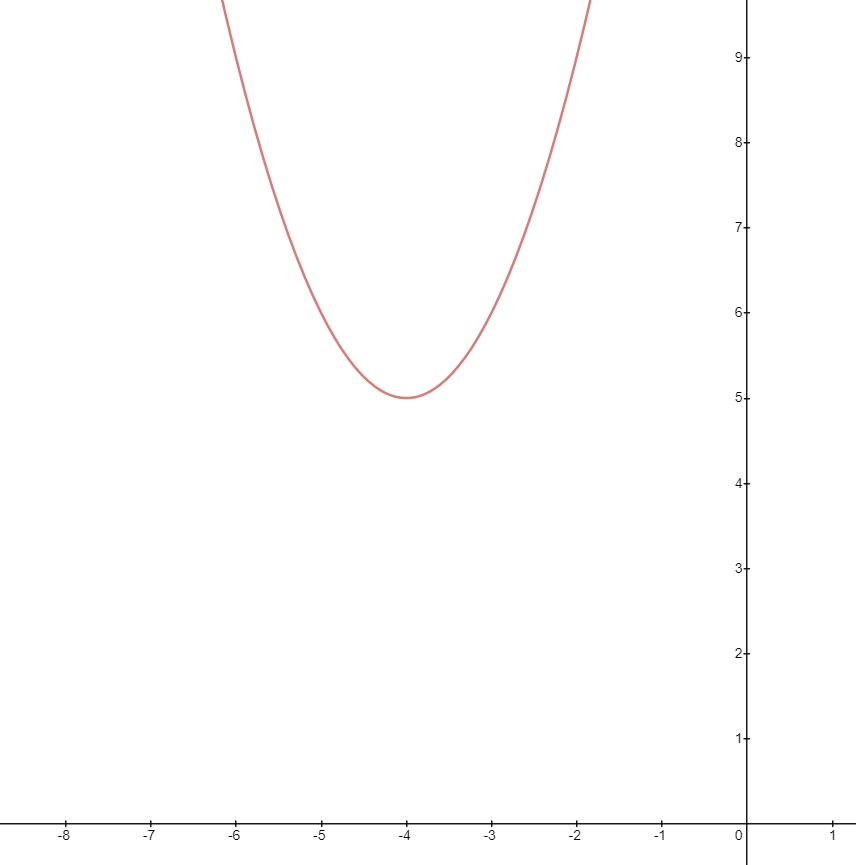
   
3. برای تعیین دامنه و بُرد تابع تصویر، انتقال های افقی و عمودی را به دامنه و برد تابع اصلی اضافه کنید. از آنجا که دامنۀ تابع اصلی شامل تمامی اعداد حقیقی می باشد، یعنی \((-\infty,\infty)\)، با افزودن چیزی به آن تغییری در آن حاصل نمی شود. برد تابع اصلی \([0,\infty)\) است که با افزودن انتقال عمودی به میزان \(5\) واحد به سمت بالا، برد تابع تصویر به \([5,\infty)\) تغییر می کند.