خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
انتقال های افقی و عمودی در توابع: تمرین 12

در این آموزش به انتقال های افقی و عمودی (Horizontal and Vertical Translations) در توابع می پردازیم.

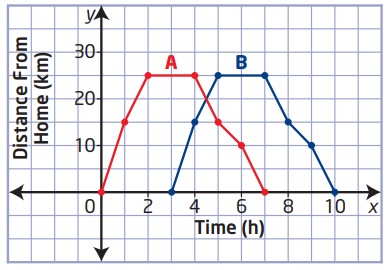
جِنی یک دوچرخه سوار مشتاق است. او بعد از اینکه تا دریاچه دوچرخه سواری کرد و به خانه برگشت، نمودار مسافتی را که رفته بود در مقابل زمان ترسیم کرد (نمودار \(\text{A}\)).

این آموزش بخشی از یک مجموعه آموزش می باشد که آموزش اول این مجموعه و فهرست آموزش های آن را می توانید در اینجا مشاهده کنید.
پرسش
جِنی یک دوچرخه سوار مشتاق است. او بعد از اینکه تا دریاچه دوچرخه سواری کرد و به خانه برگشت، نمودار مسافتی را که رفته بود در مقابل زمان ترسیم کرد (نمودار \(\text{A}\)).
-
اگر او در ساعت \(12\) ظهر خانه اش را ترک کرده باشد، به طور خلاصه یک سناریوی محتمل را برای سفر او توضیح دهید.
-
اگر نمودار این تابع به شکلی که در نمودار \(B\) مشاهده می کنید، منتقل شود، تفاوت هایی را که در سفر جِنی رُخ می دهد توصیف کنید.
-
اگر معادلۀ نمودار \(A\) را به شکل \(y=f(x)\) باشد، معادلۀ نمودار \(B\) را بنویسید.

پاسخ
-
همانطور که در نمودار \(A\) مشاهده می کنیم، برای جِنی دو ساعت طول کشیده تا به دریاچه که با خانۀ او \(25\) کیلومتر فاصله دارد برسد. به مدت \(2\) ساعت در دریاچه استراحت کرده و بعد \(3\) ساعت هم طول کشیده تا به خانه باز گردد.
بیشتر از پاسخ: اگر بخواهیم دقیقتر توصیف کنیم، رفت و برگشت او کلاً \(7\) ساعت زمان برده است، در ساعت اول \(15\) کیلومتر به سمت دریاچه دوچرخه سواری کرده است، در ساعت دوم \(10\) کیلومتر دیگر به سمت دریاچه دوچرخه سواری کرده است. ساعت سوم و چهارم یعنی به مدت دو ساعت در دریاچه خوش گذرانده و استراحت کرده است. ساعت پنجم \(10\) کیلومتر به سمت منزل دوچرخه سواری کرده است. ساعت ششم \(5\) کیلومتر دیگر به سمت خانه دوچرخه سواری کرده است. ساعت هفتم \(10\) کیلومتر دیگر نیز به سمت منزل دوچرخه سواری کرده است. موقع برگشتن مسیر دو ساعته را در سه ساعت طی کرده، ظاهراً یا خسته تر بوده که یواش تر آمده است و یا اینکه تعمداً آهسته آمده تا از مناظر بیشتر لذت ببرد، شاید هم هیچکدام از این حالات نیست و موقع رفتن خیلی ذوق داشته که گازش را گرفته و سریعتر رفته!
-
این انتقال مشابه توصیف نمودار اصلی (یعنی \(A\)) است، اینگونه می توان مسأله را تعبیر کرد که اگر او در سه ساعت بعد خانه را ترک می کرد اتفاقاتی که برای \(A\) توصیف کردیم برای او (در زمانی دیرتر) رخ می داد.
-
برای بدست آوردن معادلۀ نمودار \(B\)، با توجه به اینکه می دانیم نمودار آن، تبدیلی از نمودار \(A\) می باشد، اقدام به یافتن یک نقطۀ اصلی بر روی نمودار \(A\) و نقطۀ تصویر آن بر روی نمودار \(B\) می کنیم و سپس نگاشت \((x,y)\) آن را از روی آن بدست می آوریم.
$$
A(0,0) \to A'(3,0) \\
(x,y) \to (x+3,y)) \\
h=3, k=0 \\
y-k=f(x-h) \\
y = f(x-3)
$$
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: