اثبات اینکه زاویۀ محاطی در یک نیم دایره همیشه 90 درجه می باشد

زاویۀ محاطی در یک نیم دایره (angle inscribed in a semicircle) همیشه برابر با $90^{\circ}$ می باشد. در اینجا به اثبات این موضوع می پردازیم.

چیزی که می خواهیم ثابت کنیم اینست که زاویه ای که در بالای تصویر مشخص شده است، برابر با $90^{\circ}$ می باشد.
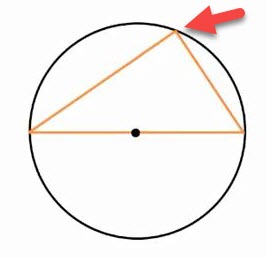
از مرکز دایره خطی را به رأس زاویه مورد نظر متصل می کنیم، این خط در واقع شعاعی از دایره می باشد.
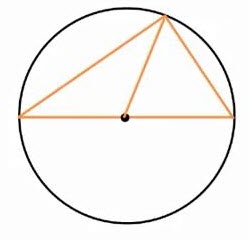
اکنون دو مثلث داریم که ابتدا به سراغ مثلث سمت چپ می رویم. از آنجا که دو ضلع این مثلث هر دو شعاعی از دایره هستند، در نتیجه یک مثلث متساوی الساقین داریم که دو زاویۀ روبروی آن با یکدیگر برابر می باشند. این دو زاویه را $x$ می نامیم.
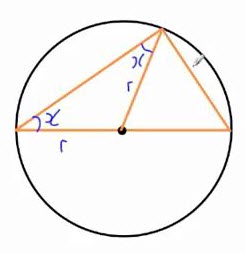
هم اکنون به سراغ مثلث سمت راست می رویم. این مثلث هم متساوی الساقین است و دو زاویۀ روبروی آن با یکدیگر برابرند. این دو زاویه را $y$ می نامیم.
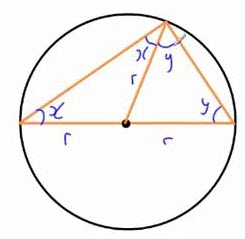
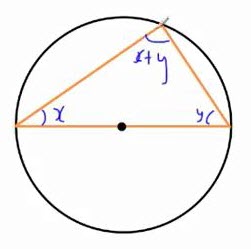
حالا آن خطی را که از مرکز به رأس زاویۀ بالا وصل کرده بودیم پاک می کنیم و نتایج را خلاصه وار می نویسیم. همانطور که در تصویر می بینید، مثلثی داریم که سه زاویۀ آن عبارت از $x$، $y$، و $x+y$ می باشند.
می دانیم که مجموع زوایای داخلی یک مثلث برابر با $180^{\circ}$ درجه می باشد، از همین موضوع برای اثبات استفاده می کنیم:
$$
x+y+(x+y)=180^{\circ}\\
2x+2y=180^{\circ}\\
\frac{2x}{2} + \frac{2y}{2} = \frac{180^{\circ}}{2}\\
x+y=90^{\circ}
$$
بنابراین اثبات می شود، صرفنظر از اینکه دو زاویۀ $x$ و $y$ چه مقادیری داشته باشند، همواره مجموع آنها برابر با $90^{\circ}$ خواهد بود.