نویسنده : امیر انصاری

1. \(AB=24 \text{ cm}\)، \(AC=34 \text{ cm}\)، و \(\angle{A} = 67^{\circ}\) . طول \(BC\) را تعیین کنید.
   
2. \(AB=15 \text{ m}\)، \(BC=8 \text{ m}\)، و \(\angle{B} = 24^{\circ}\) . طول \(AC\) را تعیین کنید.
   
3. \(AC=10 \text{ cm}\)، \(BC=9 \text{ cm}\)، و \(\angle{C} = 48^{\circ}\) . طول \(AB\) را تعیین کنید.
   
4. \(AB=9 \text{ m}\)، \(AC=12 \text{ m}\)، و \(BC=15 \text{ m}\) . اندازۀ \(\angle{B}\) را تعیین کنید.
   
5. \(AB=18.4 \text{ m}\)، \(BC=9.6 \text{ m}\)، و \(AC=10.8 \text{ m}\). اندازۀ \(\angle{A}\) را تعیین کنید.
   
6. \(AB=4.6 \text{ m}\)، \(BC=3.2 \text{ m}\)، و \(AC=2.5 \text{ m}\). اندازۀ \(\angle{C}\) را تعیین کنید.
   

پاسخ

1. 
   $$
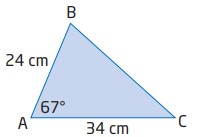   a^2 = b^2+c^2-2bc \cos A\\
   a^2 = 34^2 + 24^2 - 2(34)(24) \cos 67^{\circ}\\
   a = \sqrt{34^2 + 24^2 - 2(34)(24) \cos 67^{\circ}}\\
   a = 33.080...\\
   a \approx 33.1 \text{ cm}
   $$
   
2. 
   $$
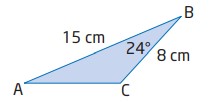   b^2 = a^2 + c^2 - 2ac \cos B\\
   b = \sqrt{a^2 + c^2 - 2ac \cos B}\\
   b = \sqrt{8^2 + 15^2 - 2(8)(15) \cos 24^{\circ}}\\
   b = 8.351...\\
   b \approx 8.4 \text{ m}
   $$
   
3. 
   $$
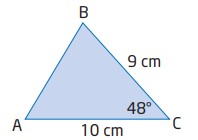   c=\sqrt{a^2+b^2-2ab \cos C}\\
   c=\sqrt{9^2+10^2-2(9)(10) \cos 48^{\circ}}\\
   c=7.781...\\
   c \approx 7.8 \text{ cm}
   $$
   
4. 
   $$
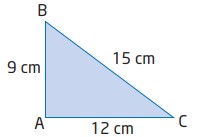   \cos B = \frac{a^2+c^2-b^2}{2ac}\\
   \angle{B} = \cos^{-1} \biggl( \frac{a^2+c^2-b^2}{2ac} \biggr)\\
   \angle{B} = \cos^{-1} \biggl( \frac{15^2+9^2-12^2}{2(15)(9)} \biggr)\\
   \angle{B} = 53.130...\\
   \angle{B} \approx 53^{\circ}
   $$
   
5. 
   $$
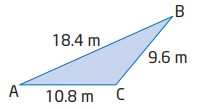   \angle{A} = \cos^{-1} \biggl( \frac{b^2+c^2-a^2}{2bc} \biggr)\\
   \angle{A} = \cos^{-1} \biggl( \frac{10.8^2+18.4^2-9.6^2}{2(10.8)(18.4)} \biggr)\\
   \angle{A} = 24.013...\\
   \angle{A} \approx 24^{\circ}
   $$
   
6. 
   $$
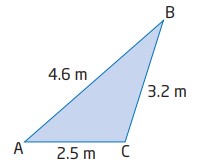   \angle{C} = \cos^{-1} \biggl( \frac{a^2+b^2-c^2}{2ab} \biggr)\\
   \angle{C} = \cos^{-1} \biggl( \frac{3.2^2+2.5^2-4.6^2}{2(3.2)(2.5)} \biggr)\\
   \angle{C} = 106.970...\\
   \angle{C} \approx 107^{\circ}
   $$