خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
حل کردن معادلات درجه دوم دارای سه جمله

معادلات درجه دوم نه تنها پایه ای برای جبر هستند، بلکه همچنین برای فیزیک، کسب و کارها، ستاره شناسی، و بسیاری کاربردهای دیگر حائز اهمیت می باشند. با حل کردن یک معادله درجه دوم (Quadratic equation)، شما به پاسخ پرسشهایی همچون این پرسشها می رسید: "چه زمانی آن سنگ به زمین برخورد می کند؟" یا "چه زمانی سود بیشتر از 100 درصد می شود؟" یا "چه زمانی در طول سال، زمین در نزدیکترین فاصله با خورشید قرار می گیرد؟"

در دو بخش قبلی، در معادله درجه دوم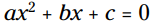 یا b و یا c برابر با 0 بودند. اکنون من اجازه نمی دهم که کسی چیزی را نادیده بگیرد. در این بخش، هر کدام از حروف a، b، و c عددی هستند که 0 نیست.
یا b و یا c برابر با 0 بودند. اکنون من اجازه نمی دهم که کسی چیزی را نادیده بگیرد. در این بخش، هر کدام از حروف a، b، و c عددی هستند که 0 نیست.
برای حل کردن یک معادله درجه دوم، منتقل کردن همه چیز به یک سمت علامت برابری و قرار دادن 0 در سمت دیگر آن، کارآمدترین روش می باشد. اگر ممکن باشد از معادله فاکتورگیری کنید، و بعد از آن از ویژگی ضرب در صفر (MPZ) بعد استفاده کنید. اگر در این وضعیت سه جمله در معادله وجود نداشته باشد، به بخش های قبلی مراجعه کنید.
در مثال زیر، لیست مراحل حل کردن یک معادله درجه دوم سه جمله ای (trinomial) را با استفاده از فاکتورگیری می بینید.
مثال: معادله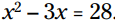 را برای x حل کنید. برای حل کردن آن از مراحل زیر پیروی کنید:
را برای x حل کنید. برای حل کردن آن از مراحل زیر پیروی کنید:
فاکتورگیری برای حل کردن معادلات درجه دوم کاملاً ساده به نظر می رسد. اما فاکتورگیری از معادلات سه جمله ای (trinomial equations) می تواند کمی سخت باشد. اگر یک معادله درجه دوم با سه جمله قابل فاکتورگیری باشد، سپس حاصلضرب دو دوجمله ای (binomials) می شود آن سه جمله ای. اگر یک معادله درجه دوم که دارای سه جمله می باشد، قابل فاکتورگیری نباشد، از فرمول معادلات درجه دوم (Quadratic Formula) که در ادامۀ همین فصل آموزش خواهیم داد، برای حل آن معادله استفاده می شود.
یادتان باشد: حاصلضرب دو دوجمله ای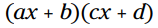 برابر با سه جمله ای
برابر با سه جمله ای 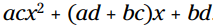 می باشد. این یک روش فانتزی برای نمایش آنچیزی که در نتیجه عملیات FOIL در زمان ضرب دو دوجمله ای در یکدیگر بدست می آورید، می باشد.
می باشد. این یک روش فانتزی برای نمایش آنچیزی که در نتیجه عملیات FOIL در زمان ضرب دو دوجمله ای در یکدیگر بدست می آورید، می باشد.
اکنون، از unFOIL استفاده می کنیم. اگر نیاز به یادآوری و مرور در مورد موضوعات FOIL و unFOIL دارید، فصل 9 را بررسی کنید.
مثالهای زیر همگی به شما نشان می دهند چگونه استفاده از فاکتورگیری و ویژگی ضرب در صفر به شما امکان می دهند تا پاسخهایی را برای یک معادله درجه دوم با تمامی سه جمله آن، بیابید.
مثال: در این معادله x را بیابید: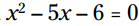
مثال: این معادله را برای x حل کنید: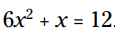
مثال: این معادله را برای y حل کنید: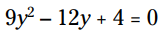
مثال: این معادله را برای z حل کنید: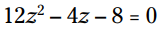
یادتان باشد: هنگامی که پاسخهایتان را درست آزمایی می کنید، همیشه از معادله اصلی استفاده کنید (نسخه ای که هنوز هیچ تغییری روی آن نداده اید).

در دو بخش قبلی، در معادله درجه دوم
برای حل کردن یک معادله درجه دوم، منتقل کردن همه چیز به یک سمت علامت برابری و قرار دادن 0 در سمت دیگر آن، کارآمدترین روش می باشد. اگر ممکن باشد از معادله فاکتورگیری کنید، و بعد از آن از ویژگی ضرب در صفر (MPZ) بعد استفاده کنید. اگر در این وضعیت سه جمله در معادله وجود نداشته باشد، به بخش های قبلی مراجعه کنید.
در مثال زیر، لیست مراحل حل کردن یک معادله درجه دوم سه جمله ای (trinomial) را با استفاده از فاکتورگیری می بینید.
مثال: معادله
-
همه جملات را به یک سمت منتقل کنید. در سمت راست 0 را تنها بگذارید.
در این مورد، شما می توانید 28 را از هر دو سمت معادله تفریق کنید:
یادتان باشد: شکل استاندارد معادله درجه دوممی باشد.
-
تمامی روشهایی را که طی آن می توانید دو عدد را در یکدیگر ضرب کنید تا به a برسید، تعیین کنید.
در معادله، داریم
، که فقط می تواند حاصلضرب 1 در خودش باشد.
-
تمامی روشهایی را که طی آن می توانید دو عدد را در یکدیگر ضرب کنید تا به c برسید، تعیین کنید (فعلاً علامت c را نادیده بگیرید).
عدد 28 می تواند حاصلضرب این اعداد باشد:
1 × 28, 2 × 14, 4 × 7
-
فاکتور بگیرید.
اگر c مثبت باشد، یک عملیات را از لیست مرحله 2 و یک عملیات را از لیست مرحله 3 انتخاب کنید به نحوی که مجموع حاصلضرب متقاطع آنها برابر با b باشد.
اگر c منفی باشد، یک عملیات را از لیست مرحله 2 و یک عملیات را از لیست مرحله 3 انتخاب کنید به نحوی که اختلاف بین حاصلضرب متقاطع آنها برابر با b باشد.
در این مسأله، c منفی می باشد، و اختلاف بین 4 و 7 برابر با 3 می باشد.
با فاکتورگیری شما خواهید داشت.
-
از ویژگی ضرب در صفر (MPZ) استفاده کنید.
یاو یا
. اکنون سعی کنید در هر کدام از این حالت ها با منزوی کردن x در یک سمت معادله مسأله را برای x حل کنید.
-
به شما نتیجه
را می دهد.
-
به شما نتیجه
را می دهد.
یا
می باشند.
-
-
پاسخ خودتان را درست آزمایی کنید.
اگر x برابر با 7 باشد، سپس خواهیم داشت:.
اگر x برابر با 4- باشد، سپس خواهیم داشت:
هر دو پاسخ درست آزمایی شدند.
فاکتورگیری برای حل کردن معادلات درجه دوم کاملاً ساده به نظر می رسد. اما فاکتورگیری از معادلات سه جمله ای (trinomial equations) می تواند کمی سخت باشد. اگر یک معادله درجه دوم با سه جمله قابل فاکتورگیری باشد، سپس حاصلضرب دو دوجمله ای (binomials) می شود آن سه جمله ای. اگر یک معادله درجه دوم که دارای سه جمله می باشد، قابل فاکتورگیری نباشد، از فرمول معادلات درجه دوم (Quadratic Formula) که در ادامۀ همین فصل آموزش خواهیم داد، برای حل آن معادله استفاده می شود.
یادتان باشد: حاصلضرب دو دوجمله ای
اکنون، از unFOIL استفاده می کنیم. اگر نیاز به یادآوری و مرور در مورد موضوعات FOIL و unFOIL دارید، فصل 9 را بررسی کنید.
مثالهای زیر همگی به شما نشان می دهند چگونه استفاده از فاکتورگیری و ویژگی ضرب در صفر به شما امکان می دهند تا پاسخهایی را برای یک معادله درجه دوم با تمامی سه جمله آن، بیابید.
مثال: در این معادله x را بیابید:
-
این معادله در شکل استاندارد معادلات درجه دوم می باشد، بنابراین شما می توانید ادامه بدهید.
-
تمامی روشهایی که می توانید دو عدد را در یکدیگر ضرب کنید تا به a برسید را تعیین کنید.
، که می تواند فقط حاصلضرب 1 در خودش باشد. اگر دو دوجمله ای داشته باشیم، فاکتورهای سمت چپ این دوجمله ای ها x خواهند بود زیرا ضریب اولین جمله 1 می باشد.
-
تمامی روشهایی را که می توانید دو عدد را در یکدیگر ضرب کنید تا به c برسید تعیین کنید.
، بنابراین، اگر از علامت c صرفنظر کنیم خواهیم داشت:
1 × 6, 2 × 3
-
فاکتور بگیرید.
برای تصمیم گیری در این مورد که کدام ترکیبها باید مورد استفاده قرار بگیرند، به علامت آخرین جمله در سه جمله ای یعنی 6 نگاه کنید، که منفی می باشد. این به شما می گوید که باید از تفاضل بین قدر مطلق دو عدد موجود در لیست استفاده کنید تا جمله وسط در سه جمله ای یعنی 5- را بدست آورید (در این مرحله علامت اعداد را در نظر نگیرید). در این مورد، یکی از ترکیبها بدرستی کار می کند، زیرا تفاضل بین آنها برابر با 5 می باشد. اگر شما از 1+ و 6- استفاده کنید، شما می توانید در فرآیند ضرب متقابل در FOIL فوراً مقدار 5- را بدست آورید. بنابراین.
-
از ویژگی ضرب در صفر استفاده کنید.
با استفاده از ویژگی ضرب در صفر،یا
. این به شما می گوید که
یا
.
-
پاسخها را درست آزمایی کنید.
اگر، سپس
اگر، سپس
هر دو پاسخ به درستی کار می کنند!
مثال: این معادله را برای x حل کنید:
-
معادله را به شکل استاندارد معادله های درجه دوم بنویسید.
اولین کاری که باید انجام بدهید اینست که 12- را به هر سمت از معادله اضافه کنید تا معادله به شکل استاندارد آن تبدیل شود، تا در نتیجه آماده فاکتورگیری و حل کردن شود:
فاکتورگیری این مورد اندکی پیچیده تر می باشد، زیرا عدد 6 که در ابتدا قرار دارد چند جفت انتخاب از فاکتورها دارد، و 12 که در انتها قرار دارد نیز چندین انتخاب دارد. مهارت شما اینست که ترکیب درستی از انتخابها را گزینش کنید.
-
تمامی ترکیبهایی که می توانند در یکدیگر ضرب شوند تا نتیجه a شود را پیدا کنید.
شما می توانید با حاصل ضربهای زیر به 6 برسید:
1 × 6, 2 × 3
-
تمامی ترکیبهایی که می توانند در یکدیگر ضرب شوند تا نتیجه c شود را پیدا کنید.
شما می توانید با حاصل ضربهای زیر به 12 برسید:
1 × 12, 2 × 6, 3 × 4
-
فاکتورگیری کنید.
شما باید فاکتورهایی را برای استفاده انتخاب کنید که تفاضل بین ضرب متقابل آنها (بیرونی و درونی) برابر با 1 ، یعنی ضریب جمله میانی گردد. چگونه این موضوع را می دانید؟ زیرا 12 منفی می باشد، و از آنجا که جمله میانی ضریبی ندارد، مقداری که در جمله میانی ضرب شده است 1 در نظر گرفته می شود.
با یک مرور سریع متوجه می شوید که استفاده از 2 و 3 در 6 و از آن سمت استفاده از 3 و 4 در 12، می توانید ترکیب مورد نظرتان را بیابید:و
. تفاضل بین 8 و 9 برابر با 1 می باشد. در مورد علامتها فعلاً نگران نباشید و در مراحل بعدی حائز اهمیت می گردند.
دوجمله ای ها را پر کنید و فاکتورها را به خط کنید تا 2 در 4 ضرب شود و 3 در 3 ضرب گردد، و شما یک 6 در ابتدا و یک 12 در انتها داشته باشید. اوه!
این معادله درجه دوم یک علامت + در جمله میانی دارد، بنابراین من نیاز دارم که عدد بزرگتر حاصلضرب بیرونی و درونی مثبت باشد. من با مثبت کردن علامت 9x به این هدف می رسم، که با مثبت بودن 3 و منفی بودن 4 به آن می رسیم.
-
از ویژگی ضرب در صفر برای حل کردن معادله استفاده کیند.
این سه جمله ای فاکتورگیری شد. ویژگی ضرب در صفر به شما می گوید که یاو یا
. اگر
سپس
یا
. اگر
سپس
یا
.
-
پاسختان را درست آزمایی کنید.
وقتیکه، سپس:
وقتیکه
، سپس:
مثال: این معادله را برای y حل کنید:
-
این معادله هم اکنون در شکل استاندارد آن می باشد.
-
تمامی اعدادی را که حاصلضرب آنها a می شود بیابید.
فاکتورهای 9 عبارتند از:
1 × 9, 3 × 3
-
تمامی اعدادی را که حاصلضرب آنها c می شود بیابید.
فاکتورهای 4 عبارتند از:
1 × 4, 2 × 2
-
فاکتورگیری کنید.
ترکیب 3 در 3 همراه با ترکیب 2 در 2 آنچیزی است که درست کار می کند، زیرا حاصلضرب متقابل هر دوی آنها 6 می شود و شما در اینجا نیاز به دو حاصلضرب دارید که مجموعشان برابر با 12 گردد. بنابراین:
توجه داشته باشید که من علامتهای منفی را قرار دادم، زیرا 12 نیاز به این دارد که یک مجموع منفی باشد.
-
از ویژگی ضرب در صفر (MPZ) برای حل مسأله استفاده کنید.
هر دو فاکتور در اینجا یکسان می باشند. این موضوع به این معنا می باشد که استفاده از ویژگی ضرب در صفر یک پاسخ یکسان را دو مرتبه به شما می دهد. هنگامیکه، این معادله را برای y حل کنید. ابتدا 2 را به هر دو سمت معادله بیفزایید، و سپس آن را بر 3 تقسیم کنید. پاسخ
می باشد. این یک ریشۀ مضاعف (double root) می باشد، که، از نظر فنی یک پاسخ دارد، اما دو مرتبه اتفاق می افتد.
نکات فنی: یک ریشۀ مضاعف (double root) در معادلات درجه دوم سه جمله ای که از دوجمله ای های مربع کامل آمده اند، اتفاق می افتد. اگر در زمینه دوجمله ای های مربع کامل (Perfect-square binomials) نیاز به یک یادآوری دارید، در فصل 7 می توانید مباحث مربوطه را بیابید. این مربع های کامل دوجمله ای چیزی فراتر از حاصلضرب یک دوجمله ای در خودش نمی باشند. به همین دلیل است که وقتی آنها را فاکتورگیری می کنیم، تنها یک پاسخ وجود دارد - آن پاسخ برای هر یک از این دوجمله ای ها یکسان می باشد.
مثال: این معادله را برای z حل کنید:
-
این معادله درجه دوم هم اکنون در شکل استاندارد می باشد.
شما می توانید با جستجو برای ترکیبهایی از فاکتورهای 12 و 8 کار را آغاز کنید، اما ممکن است متوجه شده باشید که هر سه جمله بر 4 بخش پذیر می باشند. برای اینکه کارها راحتتر شود، ابتدا بزرگترین فاکتور مشترک (GCF) را بیرون بکشید، و سپس با اعداد کوچکتر داخل پرانتز کار کنید.
-
اعدادی را پیدا کنید که حاصلضربشان 3 می شود.
-
اعدادی را پیدا کنید که حاصلضربشان 2 می شود.
-
فاکتورگیری کنید.
این واقعاً فوق العاده است، مخصوصاً اینکه 3 و 2 هر دو عدد اول می باشند و تنها به یک روش قابل فاکتورگیری هستند. تنها کار مشکل شما اینست که فاکتورها را به نحوی به خط کنید که تفاضل بین حاصلضرب متقابل آنها برابر با 1 باشد.
از آنجا که جمله میانی منفی می باشد، شما نیاز دارید که حاصلضرب بزرگتر را منفی کنید، بنابراین علامت منفی را به 1 بدهید.
-
از ویژگی ضرب در صفر (MPZ) برای حل کردن مقدار z استفاده کنید.
این بار، هنگامی که از ویژگی ضرب در صفر استفاده می کنید، سه فاکتور دارید که باید آنها را لحاظ کنید.
اولین معادله غیر ممکن می باشد. 4 هرگز برابر با 0 نمی باشد. اما آن دو معادله دیگر پاسخها را به شما می دهند. اگر
، سپس
-
پاسخها را درست آزمایی کنید.
یادتان باشد: هنگامی که پاسخهایتان را درست آزمایی می کنید، همیشه از معادله اصلی استفاده کنید (نسخه ای که هنوز هیچ تغییری روی آن نداده اید).
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: