خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
فرمول حل معادله درجه دوم (Quadratic Formula)
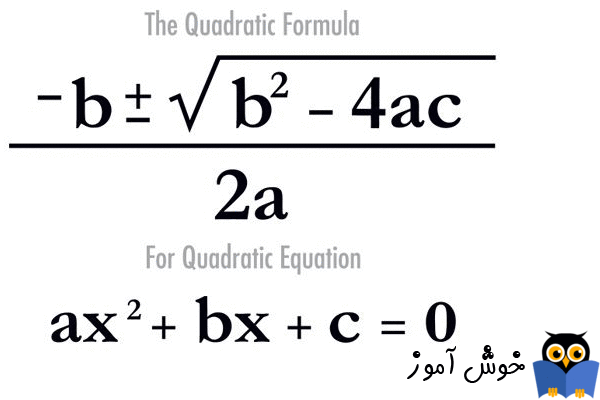
فرمول حل معادله درجه دوم (Quadratic Formula) مخصوص معادلات درجه دوم می باشد. یک معادله درجه دوم، می تواند تا دو پاسخ داشته باشد، اما ممکن است فقط یک پاسخ و یا حتی هیچ پاسخی در کل وجود نداشته باشد.

یادتان باشد: در یک معادله درجه دوم با شکل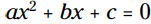 مقادیر a، b، و c می توانند هر عدد حقیقی (real number) باشند. a نمی تواند برابر با 0 باشد، اما b و c می توانند برابر با 0 باشند.
مقادیر a، b، و c می توانند هر عدد حقیقی (real number) باشند. a نمی تواند برابر با 0 باشد، اما b و c می توانند برابر با 0 باشند.
فرمول حل معادله درجه دوم (Quadratic Formula) به شما امکان می دهد تا در مواقعی که معادله ها زیاد زیبا نباشند، پاسخهایی را پیدا کنید. اعداد زمانی زیبا نیستند که کسرهای بدشکلی باشند، اعداد اعشاری نامناسب و بدون انتها باشند، و یا رادیکال های زمخت باشند.
قوانین جبر: فرمول حل معادله درجه دوم (Quadratic Formula) به شما می گوید اگر یک معادله در شکل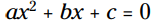 باشد، سپس پاسخهای آن، یعنی مقادیر x می تواند از طریق فرمول زیر بدست آید.
باشد، سپس پاسخهای آن، یعنی مقادیر x می تواند از طریق فرمول زیر بدست آید.
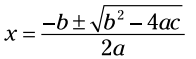
شما یک علامت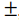 در فرمول می بینید. این نماد یک خلاصه نویسی برای گفتن این مطلب است که این معادله می تواند به دو معادله جداگانه شکسته شود، که یکی از آنها از نماد بعلاوه و دیگری از نماد منها استفاده می کند. این دو معادله جداگانه را در زیر می بینید:
در فرمول می بینید. این نماد یک خلاصه نویسی برای گفتن این مطلب است که این معادله می تواند به دو معادله جداگانه شکسته شود، که یکی از آنها از نماد بعلاوه و دیگری از نماد منها استفاده می کند. این دو معادله جداگانه را در زیر می بینید:

آیا می توانید تفاوت بین این دو معادله را ببینید؟ تنها تفاوت تغییر علامت بعلاوۀ قبل از رادیکال به علامت منها می باشد.
شما می توانید این فرمول را روی هر معادله درجه دوم بکار ببرید تا پاسخهایش را بدست آورید - خواه آن معادله فاکتورگیری شده باشد یا نه. اجازه بدهید چند مثال از چگونگی کارکرد این فرمول را به شما نشان بدهم.
مثال: این معادله را با فرمول حل معادله درجه دوم، حل کنید: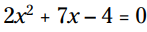
با اشاره به، شکل استاندارد یک معادله درجه دوم که در آن ضریب x2 برابر با a می باشد، ضریب x برابر با b می باشد، و ثابت برابر با c می باشد. در این مورد، a = 2 و b = 7 و c = -4 است. با وارد کردن این اعداد در فرمول، خواهید داشت:

اکنون، ساده سازی کنید، و به ترتیب عملیات دقت کنید، خواهید داشت:
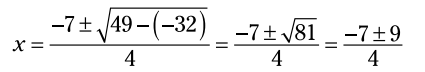
با بکار بردن + در مقابل عدد 9 و سپس بکار بردن - در مقابل عدد 9، دو پاسخ را بدست می آورید.
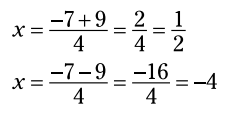
هرگاه پاسخهای بدست آمده از فرمول حل معادله درجه دوم، اعداد صحیح (integers) یا کسر (fractions) باشند، به این معنا می باشد که سه جمله ای (trinomial) مربوطه می تواند فاکتورگیری شود. با این حال، این به این معنا نمی باشد که شما نمی توانید فرمول درجه دوم را روی مسأله های قابل فاکتورگیری استفاده کنید. گاهی اوقات ساده تر اینست که فرمول را در صورتیکه معادله دارای اعداد طولانی و بدشکل باشد، استفاده کنید. با این وجود، به طور کلی روش سریعتر اینست که هر جا که ممکن باشد، با استفاده از عملیات unFOIL و سپس ویژگی ضرب در صفر (MPZ) معادله درجه دوم را حل کنید:
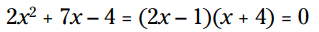
سپس با استفاده از ویژگی ضرب در صفر (MPZ)، شما خواهید داشت:

خوب، اگر معادله قابل فاکتورگیری نباشد، نتایج به چه شکلی خواهند بود؟ مثال بعدی به شما نشان می دهد.
مثال: با استفاده از فرمول معادلات درجه دوم این معادله را برای x حل کنید: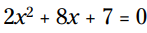
در این مسأله، شما در هنگام استفاده از فرمول از این مقادیر استفاده می کنید:
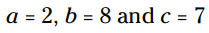
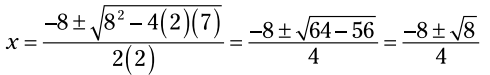
رادیکال می تواند ساده سازی شود، زیرا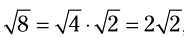 ، بنابراین:
، بنابراین:
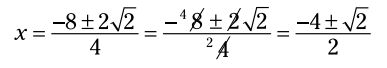
در اینجا معادل اعشاری این پاسخها را می بینید:
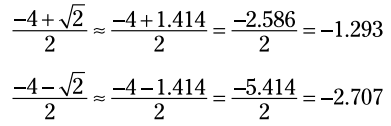
هنگام درست آزمایی این پاسخها، برآوردها چه کاری انجام می دهند؟ اگر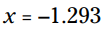 ، سپس:
، سپس:
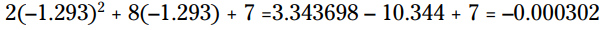
نتیجه 0 نشد! چه اتفاقی افتاد؟ آیا پاسخ اشتباه است؟ نه، پاسخ درست است. گرد کردن منجر به این خطا شده است که پاسخ به صورت دقیق ظاهر نشود. این مشکل زمانی پیش می آید که شما به جای استفاده از شکل رادیکالی عدد از مقدار گرد شده آن استفاده کنید. در اینجا یک برآورد برای پاسخ استفاده شده است زیرا جذر یک عدد که مربع کامل نباشد یک عدد گنگ می باشد، و مقدار اعشاری هرگز خاتمه نمی یابد. گرد کردن یک عدد اعشاری تا سه مرتبه اعشاری (decimal places) به نظر می رسد که کفایت کند.

یادتان باشد: در یک معادله درجه دوم با شکل
فرمول حل معادله درجه دوم (Quadratic Formula) به شما امکان می دهد تا در مواقعی که معادله ها زیاد زیبا نباشند، پاسخهایی را پیدا کنید. اعداد زمانی زیبا نیستند که کسرهای بدشکلی باشند، اعداد اعشاری نامناسب و بدون انتها باشند، و یا رادیکال های زمخت باشند.
قوانین جبر: فرمول حل معادله درجه دوم (Quadratic Formula) به شما می گوید اگر یک معادله در شکل
شما یک علامت
آیا می توانید تفاوت بین این دو معادله را ببینید؟ تنها تفاوت تغییر علامت بعلاوۀ قبل از رادیکال به علامت منها می باشد.
شما می توانید این فرمول را روی هر معادله درجه دوم بکار ببرید تا پاسخهایش را بدست آورید - خواه آن معادله فاکتورگیری شده باشد یا نه. اجازه بدهید چند مثال از چگونگی کارکرد این فرمول را به شما نشان بدهم.
مثال: این معادله را با فرمول حل معادله درجه دوم، حل کنید:
با اشاره به، شکل استاندارد یک معادله درجه دوم که در آن ضریب x2 برابر با a می باشد، ضریب x برابر با b می باشد، و ثابت برابر با c می باشد. در این مورد، a = 2 و b = 7 و c = -4 است. با وارد کردن این اعداد در فرمول، خواهید داشت:
اکنون، ساده سازی کنید، و به ترتیب عملیات دقت کنید، خواهید داشت:
با بکار بردن + در مقابل عدد 9 و سپس بکار بردن - در مقابل عدد 9، دو پاسخ را بدست می آورید.
هرگاه پاسخهای بدست آمده از فرمول حل معادله درجه دوم، اعداد صحیح (integers) یا کسر (fractions) باشند، به این معنا می باشد که سه جمله ای (trinomial) مربوطه می تواند فاکتورگیری شود. با این حال، این به این معنا نمی باشد که شما نمی توانید فرمول درجه دوم را روی مسأله های قابل فاکتورگیری استفاده کنید. گاهی اوقات ساده تر اینست که فرمول را در صورتیکه معادله دارای اعداد طولانی و بدشکل باشد، استفاده کنید. با این وجود، به طور کلی روش سریعتر اینست که هر جا که ممکن باشد، با استفاده از عملیات unFOIL و سپس ویژگی ضرب در صفر (MPZ) معادله درجه دوم را حل کنید:
سپس با استفاده از ویژگی ضرب در صفر (MPZ)، شما خواهید داشت:
خوب، اگر معادله قابل فاکتورگیری نباشد، نتایج به چه شکلی خواهند بود؟ مثال بعدی به شما نشان می دهد.
هشدار: در اینجا دو چیز هست که در هنگام استفاده از فرمول حل کردن معادلات درجه دوم باید مراقبشان باشید:
-
فراموش نکنید که b- به معنای استفاده از مخالف b می باشد.
اگر ضریب b در شکل استاندارد معادله یک عدد مثبت باشد، قبل از اینکه آن را در فرمول وارد کنید، آن را به یک عدد منفی تبدیل کنید. اگر b منفی باشد، سپس آن را در فرمول به یک عدد مثبت تبدیل کنید.
-
هنگام ساده سازی عدد زیر رادیکال دقت کنید.
ترتیب عملیات (order of operations) به شما می گوید که ابتدا باید مقدار b را مربع کنید، و سپس سه فاکتور دیگر را در یکدیگر ضرب کنید، و بعد از آن آنها را از مربع b تفریق کنید. اگر شما دقت نکنید برخی از اشتباهات در مورد علامتها، ممکن است روی بدهند.
مثال: با استفاده از فرمول معادلات درجه دوم این معادله را برای x حل کنید:
در این مسأله، شما در هنگام استفاده از فرمول از این مقادیر استفاده می کنید:
رادیکال می تواند ساده سازی شود، زیرا
هشدار: هنگام ساده سازی این عبارت مراقب باشید: 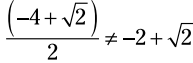 . هر دو جمله موجود در صورت کسر باید بر 2 تقسیم گردند.
. هر دو جمله موجود در صورت کسر باید بر 2 تقسیم گردند.
در اینجا معادل اعشاری این پاسخها را می بینید:
هنگام درست آزمایی این پاسخها، برآوردها چه کاری انجام می دهند؟ اگر
نتیجه 0 نشد! چه اتفاقی افتاد؟ آیا پاسخ اشتباه است؟ نه، پاسخ درست است. گرد کردن منجر به این خطا شده است که پاسخ به صورت دقیق ظاهر نشود. این مشکل زمانی پیش می آید که شما به جای استفاده از شکل رادیکالی عدد از مقدار گرد شده آن استفاده کنید. در اینجا یک برآورد برای پاسخ استفاده شده است زیرا جذر یک عدد که مربع کامل نباشد یک عدد گنگ می باشد، و مقدار اعشاری هرگز خاتمه نمی یابد. گرد کردن یک عدد اعشاری تا سه مرتبه اعشاری (decimal places) به نظر می رسد که کفایت کند.
یادتان باشد: شما نباید انتظار داشته باشید این درست آزمایی دقیقاً برابر با 0 گردد. به طور کلی، اگر شما عددی را که از نتیجه درست آزمایی تان به دست می آورید، به همان تعداد مرتبه اعشاری که رادیکال را گرد نموده بودید، گرد کنید، سپس باید آن 0 را که منتظرش بودید بدست آورید.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (1 دیدگاه)
دیدگاه خود را ثبت کنید: