خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
کاربردهای معادلات درجه دوم
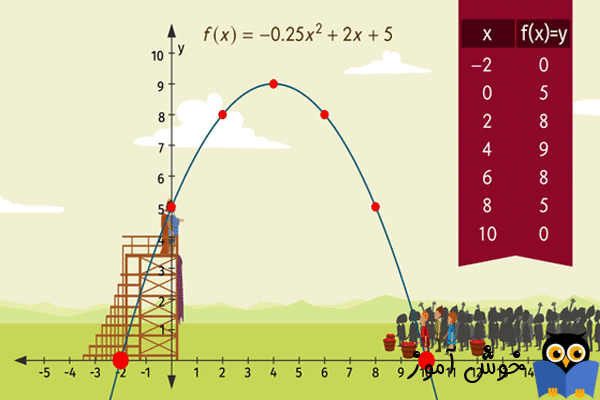
معادلات درجه دوم (Quadratic equations) در بسیاری از کاربردهای ریاضی، علوم، و کسب و کارها یافت می شوند. به همین دلیل هم هست که آنها را اینقدر مورد مطالعه قرار می دهند. گراف های (graphs) معادلات درجه دو همیشه به شکل U می باشند، با یک نقطۀ انتهایی (extreme point) که در بالاترین، پایینترین، دورترین در سمت چپ، یا دورترین در سمت راست می باشد. این نقطۀ انتهایی (extreme point) معمولاً پاسخ به سوال در مورد وضعیتی که توسط معادله درجه دوم مدل شده است، می باشد. در سایر کاربردها، شما نقاطی را می خواهید که منحنی U شکل از یک محور عبور کرده است. آن نقاط (points) با پیدا کردن پاسخهایی برای معادله درجه دوم در حالتی که برابر 0 قرار داده شده است، یافت می گردند. در این بخش، به شما چند مثال از چگونگی استفاده از معادلات درجه دوم در کاربردهای واقعی را نشان می دهم.

در فیزیک، یک معادله که به شما می گوید یک شیء بعد از مقدار مشخصی از زمان در چه ارتفاعی قرار دارد می تواند به شکل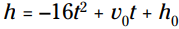 نوشته شود. در این معادله، مقدار
نوشته شود. در این معادله، مقدار 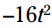 بخشی است که نیروی گرانش بر روی جسم را محاسبه می کند. عددی که با
بخشی است که نیروی گرانش بر روی جسم را محاسبه می کند. عددی که با 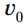 نمایش داده می شود شتاب اولیه می باشد - که سرعت خیلی ابتدایی می باشد.
نمایش داده می شود شتاب اولیه می باشد - که سرعت خیلی ابتدایی می باشد. 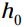 ارتفاع اولیه می باشد - ارتفاع (در واحد فوت) ساختمان، صخره، یا چارپایه که از آنجا شیء مربوطه پرتاب، شلیک، یا رها می شود. متغیر t نماینده زمان می باشد - چند ثانیه یا دقیقه گذشته است.
ارتفاع اولیه می باشد - ارتفاع (در واحد فوت) ساختمان، صخره، یا چارپایه که از آنجا شیء مربوطه پرتاب، شلیک، یا رها می شود. متغیر t نماینده زمان می باشد - چند ثانیه یا دقیقه گذشته است.
مثال: یک سنگ از بالای یک ساختمان 40 فوتی به سمت بالا پرتاب می شود.سرعت اولیه آن سنگ 128 فوت در ثانیه می باشد. چه زمانی سنگ به ارتفاع 296 فوتی در هوا می رسد؟
ارتفاع (h) را با 296 ، و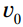 را با 128، و
را با 128، و 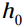 را با 40 جایگزین کنید. این معادله اکنون به این شکل نشان داده می شود:
را با 40 جایگزین کنید. این معادله اکنون به این شکل نشان داده می شود: 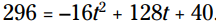 . شما می توانید طی مراحل زیر آن را حل کنید:
. شما می توانید طی مراحل زیر آن را حل کنید:
مثال بعدی وارد جنبه کسب و کار این معادلات می شود. سود بدست آمده از تولید و فروش محصولات با تفریق هزینه ها از درآمدها محاسبه می گردد. معادلاتی می توانند به عنوان مدل برای میزان سود بر مبنای تعداد اقلام تولید شده و فروخته شده باشند. مثال بعدی به شما نشان می دهد یک مدل چگونه کار می کند.
مثال: سود حاصل از تولید و فروش محصولات یک شرکت تولید کننده دمپایی با استفاده از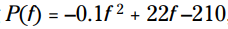 تعیین می شود، در این فرمول f نماینده تعداد جفت دمپایی ها می باشد. چه میزانی دمپایی باید تولید شده و به فروش برسد تا به یک سود مثبت برسند؟
تعیین می شود، در این فرمول f نماینده تعداد جفت دمپایی ها می باشد. چه میزانی دمپایی باید تولید شده و به فروش برسد تا به یک سود مثبت برسند؟
گراف تابع سود، یک گراف منحنی U شکل (parabola) - به این گراف شلجمی نیز می گویند - می باشد، که سمت باز آن رو به پایین است. (برای کسب اطلاعات بیشتر در مورد این گراف ها به فصل 19 مراجعه کنید.) آنچیزی را که شما نیاز دارید تا پیدا کنید، اینست که چه زمانی سود از منفی به مثبت می رود و دوباره به منفی باز می گردد. (سود زمانی کاهش می یابد که میزان اضافه کاری خیلی بالا باشد یا اینکه بسیاری از اقلام مورد نیاز به صورت برون سپاری تولید گردند.) هنگامی که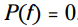 ، تابع از مثبت به منفی و از منفی به مثبت تغییر می کند. بنابراین پاسخ با حل کردن این معادله درجه دوم بدست می آید:
، تابع از مثبت به منفی و از منفی به مثبت تغییر می کند. بنابراین پاسخ با حل کردن این معادله درجه دوم بدست می آید: 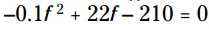 .
.
اولین کاری که باید انجام بدهید اینست که 0.1- را از هر جمله فاکتور بگیرید. اگر ضریب ابتدایی منفی باشد عملیات فاکتورگیری با unFOIL مشکل می شود، همچنین اگر مقداری کسری یا اعشاری در ضریب ها باشد، این عملیات حتی سختتر هم می گردد. با فاکتورگیری از 0.1- شما خواهید داشت:
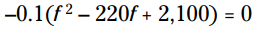
برای فاکتورگیری سه جمله ای درجه دوم، باید دو فاکتور از 2100 پیدا کنید که مجموع آنها 220 گردد. این دو فاکتور 210 و 10 می باشند. با فاکتورگیری این عبارت درجه دوم خواهید داشت:
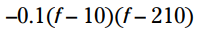
با استفاده از ویژگی ضرب در صفر (MPZ) شما در مواقعی که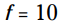 یا
یا 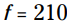 به سود 0 می رسید. و من به شما نشان می دهم که برای اعداد بین 10 و 210 سود مثبت می باشد (و در غیر اینصورت منفی می باشد). در اینجا برخی از مقادیر این تابع را می بینید:
به سود 0 می رسید. و من به شما نشان می دهم که برای اعداد بین 10 و 210 سود مثبت می باشد (و در غیر اینصورت منفی می باشد). در اینجا برخی از مقادیر این تابع را می بینید:
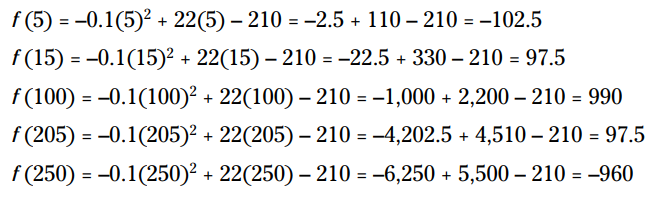

در فیزیک، یک معادله که به شما می گوید یک شیء بعد از مقدار مشخصی از زمان در چه ارتفاعی قرار دارد می تواند به شکل
مثال: یک سنگ از بالای یک ساختمان 40 فوتی به سمت بالا پرتاب می شود.سرعت اولیه آن سنگ 128 فوت در ثانیه می باشد. چه زمانی سنگ به ارتفاع 296 فوتی در هوا می رسد؟
ارتفاع (h) را با 296 ، و
-
معادله را در شکل استاندارد بنویسید.
مقدار 296- را به هر دو سمت معادله اضافه کنید.
-
بزرگترین فاکتور مشترک (GCF) را فاکتور بگیرید.
در این مورد GCF برابر با 16- می باشد.
-
سه جمله ای درجه دوم داخل پرانتز را فاکتور بگیرید.
-
از ویژگی ضرب در صفر (MPZ) برای حل کردن مسأله استفاده کنید.
بعد از 4 ثانیه، سنگ مربوطه در ارتفاع 296 فوتی در هوا خواهد بود.
یادداشت مترجم: چیزی که با نام اختصاری GCF در قسمتهای مختلف این کتاب نشان داده شده است در واقع علامت اختصاری "بزرگترین فاکتور مشترک" می باشد. به آن "بزرگترین عامل مشترک" و همینطور "بزرگترین مقسوم علیه مشترک" نیز گفته می شود. اگر جایی "ب.م.م" هم دیدید، بدانید منظور همان GCF است. بنده به خاطر اینکه ادبیات جهانی ریاضی در ذهن خواننده شکل بگیرد ترجیحم همواره بر اینست که از اسامی استاندارد و شناخته شده جهانی به جای واژگان محلی استفاده کنم.
مثال بعدی وارد جنبه کسب و کار این معادلات می شود. سود بدست آمده از تولید و فروش محصولات با تفریق هزینه ها از درآمدها محاسبه می گردد. معادلاتی می توانند به عنوان مدل برای میزان سود بر مبنای تعداد اقلام تولید شده و فروخته شده باشند. مثال بعدی به شما نشان می دهد یک مدل چگونه کار می کند.
مثال: سود حاصل از تولید و فروش محصولات یک شرکت تولید کننده دمپایی با استفاده از
گراف تابع سود، یک گراف منحنی U شکل (parabola) - به این گراف شلجمی نیز می گویند - می باشد، که سمت باز آن رو به پایین است. (برای کسب اطلاعات بیشتر در مورد این گراف ها به فصل 19 مراجعه کنید.) آنچیزی را که شما نیاز دارید تا پیدا کنید، اینست که چه زمانی سود از منفی به مثبت می رود و دوباره به منفی باز می گردد. (سود زمانی کاهش می یابد که میزان اضافه کاری خیلی بالا باشد یا اینکه بسیاری از اقلام مورد نیاز به صورت برون سپاری تولید گردند.) هنگامی که
اولین کاری که باید انجام بدهید اینست که 0.1- را از هر جمله فاکتور بگیرید. اگر ضریب ابتدایی منفی باشد عملیات فاکتورگیری با unFOIL مشکل می شود، همچنین اگر مقداری کسری یا اعشاری در ضریب ها باشد، این عملیات حتی سختتر هم می گردد. با فاکتورگیری از 0.1- شما خواهید داشت:
برای فاکتورگیری سه جمله ای درجه دوم، باید دو فاکتور از 2100 پیدا کنید که مجموع آنها 220 گردد. این دو فاکتور 210 و 10 می باشند. با فاکتورگیری این عبارت درجه دوم خواهید داشت:
با استفاده از ویژگی ضرب در صفر (MPZ) شما در مواقعی که
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: