خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
تمرین 77، ترکیب توابع؛ جابجایی و تغییر مقیاس نمودارها

فرض کنید که \(f\) یک تابع زوج و \(g\) یک تابع فرد باشد و هر دو تابع \(f\) و \(g\) بر روی خط اعداد حقیقی \((-\infty,\infty)\) تعریف شده باشند. در این صورت کدام یک از موارد زیر زوج و کدام یک فرد می باشند؟

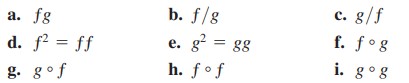
با توجه به اینکه در صورت مسئله گفته شده \(f\) یک تابع زوح و \(g\) تابعی فرد می باشد، روابط زیر را به عنوان داده های مسئله در اختیار داریم:
$$
f(-x) = f(x)\\
g(-x) = -g(x)
$$
از همین داده ها برای کشف مجهولات استفاده خواهیم کرد.

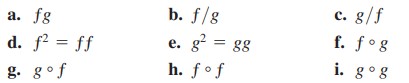
پاسخ
با توجه به اینکه در صورت مسئله گفته شده \(f\) یک تابع زوح و \(g\) تابعی فرد می باشد، روابط زیر را به عنوان داده های مسئله در اختیار داریم:
$$
f(-x) = f(x)\\
g(-x) = -g(x)
$$
از همین داده ها برای کشف مجهولات استفاده خواهیم کرد.
-
$$
(fg)(-x) = f(-x) \cdot g(-x) = f(x) \cdot (-g(x)) = (-fg)(x)\\
\Rightarrow (fg)(x) = (-fg)(x)
$$
در نتیجه \(fg\) فرد است.
-
$$
(\frac{f}{g})(-x) = \frac{f(-x)}{g(-x)} = \frac{f(x)}{-g(x)} = -(\frac{f}{g})(x)\\
\Rightarrow (\frac{f}{g})(-x) =-(\frac{f}{g})(x)
$$
در نتیجه \(\frac{f}{g}\) فرد است.
-
$$
(\frac{g}{f})(-x) = \frac{g(-x)}{f(-x)} = \frac{-g(x)}{f(x)} = -(\frac{g}{f})(x)\\
\Rightarrow (\frac{g}{f})(-x) =-(\frac{g}{f})(x)
$$
در نتیجه \(\frac{g}{f}\) فرد است.
-
$$
f^2(-x) = f(-x)f(-x) = f(x)f(x) = f^2(x)\\
\Rightarrow f^2(-x) = f^2(x)
$$
در نتیجه \(f^2\) زوج است.
-
$$
g^2(-x) = g(-x)g(-x) = (-g(x)) (-g(x)) = g^2(x)\\
\Rightarrow g^2(-x) = g^2(x)
$$
در نتیجه \(g^2\) زوج است.
-
$$
(f \circ g)(-x) = f(g(-x)) = f(-g(x)) = f(g(x)) = (f \circ g)(x)\\
\Rightarrow (f \circ g)(-x) = (f \circ g)(x)
$$
در نتیجه \(f \circ g\) زوج است.
-
$$
(g \circ f)(-x) = g(f(-x)) = g(f(x)) = (g \circ f)(x)\\
\Rightarrow (g \circ f)(-x) = (g \circ f)(x)
$$
در نتیجه \(g \circ f\) زوج می باشد.
-
$$
(f \circ f)(-x) = f(f(-x)) = f(f(x)) = (f \circ f)(x)\\
\Rightarrow (f \circ f)(-x) = (f \circ f)(x)
$$
در نتیجه \(f \circ f\) زوج می باشد.
-
$$
(g \circ g)(-x) = g(g(-x)) = g(-g(x)) = -g(g(x)) = -(g \circ g)(x)\\
\Rightarrow (g \circ g)(-x) = -(g \circ g)(x)
$$
در نتیجه \(g \circ g\) فرد است.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: