خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
تعاریف اولیۀ هندسه
در این بخش به مفاهیم پایه ای و تعاریف اولیۀ هندسه می پردازیم. این فصل باید خیلی آسان باشد، اما آن را نادیده نگیرید ـــ مگر اینکه همین الان یک نابغۀ هندسه باشید ـــ زیرا بسیاری از ایده هایی که در اینجا دریافت می کنید برای درک بقیۀ این کتاب حیاتی هستند.

مطالعۀ هندسه با تعریف پنج شیء سادۀ هندسی آغاز می گردد: نقطه (point)، خط (line)، پاره خط (segment)، نیم خط (ray)، و زاویه (angle). و من دو تعریف دیگر نیز به آن اضافه می کنم: صفحه (plane) و فضای سه بعدی (\(\text{3-D space}\)). در مجموع، این جملات شما را از بدون بُعد به سه بُعد می برند.
در اینجا تعاریف پاره خط، نیم خط، زاویه، صفحه، و فضای سه بعدی را می بینید، همینطور مفاهیم بدون تعریف نقطه و خط را نیز خواهید شناخت (دو مفهوم نقطه و خط از لحاظ فنی بدون تعریف و یا غیرقابل تعریف می باشند).
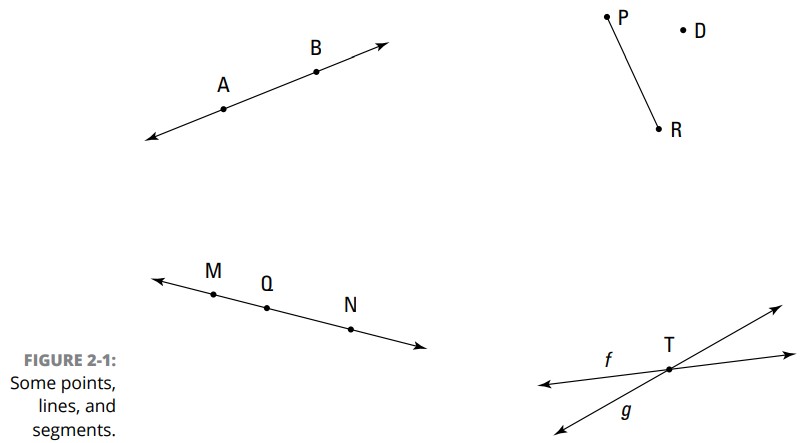
یک نقطه همانند یک لکه خیلی کوچک است، با این تفاوت که در حقیقت هیچ اندازه ای ندارد؛ یا می توانید اینطور بگویید که نقطه بی نهایت کوچک است. اساساً ابعاد یک نقطه صفر می باشد، بدون هیچ ارتفاع، طول، یا عرض. اما شما آن را مانند یک لکه ترسیم می کنید. شما نقطه ها را با حروف بزرگ نشان می دهید، مانند نقطه های \(A\)، \(D\)، و \(T\) در شکل 1-2 .
خط شبیه یک سیم نازک و راست است (اگرچه در حقیقت بی نهایت نازک است ـــ یا بهتر است بگوییم، به هیچ وجه عرضی ندارد). خطها دارای طول می باشند، بنابراین آنها دارای یک بعد (one-dimensional) هستند. یادتان باشد که یک خط در هر دوسمت آن تا ابد پیش می رود، به همین دلیل هم هست که از یک فلش دوسرِ کوچک برای نشان دادن خط \(\overleftrightarrow{AB}\) استفاده می کنید. (این نماد به صورت خط \(AB\) خوانده می شود).
شکل 1-2 را دوباره بررسی کنید. خطها معمولاً با استفاده از هر دو نقطه ای بر روی آنها نامگذاری می شوند، ترتیب قرار گیری این حروف در نامگذاری خط حائز اهمیت نیست. بنابراین خط \(\overleftrightarrow{MQ}\) با خط \(\overleftrightarrow{QM}\) یکسان می باشند، خط \(\overleftrightarrow{MN}\) همان خط \(\overleftrightarrow{NM}\) است، و \(\overleftrightarrow{QN}\) همان \(\overleftrightarrow{NQ}\) می باشد. گاهی اوقات، خطها را با یک حرف کوچک و تنها و با حروف کج نامگذاری می کنند، مانند خطهای \(f\) و \(g\) .
یک پاره خط، بخشی از یک خط است که دارای دو نقطۀ پایانی می باشد. شکل 1-2 را دوباره ببینید. اگر یک پاره خط از \(P\) به \(R\) برود، شما آن را پاره خط \(PR\) می نامید و به شکل \(\overline{PR}\) می نویسید. شما همچنین می توانید ترتیب حروف را تعویض کنید و آن را \(\overline{RP}\) بنامید. همچنین پاره خطها می توانند درون خطها ظاهر شوند، مانند \(\overline{MN}\) .
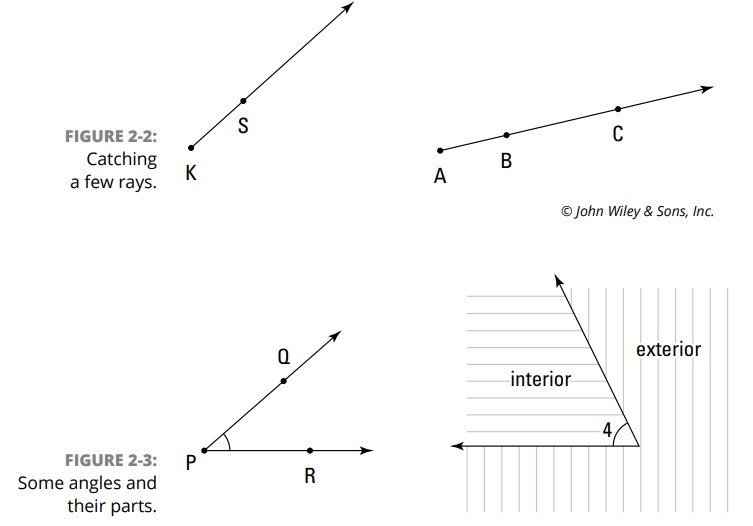
نیم خط بخشی از یک خط می باشد (به نوعی نصف یک خط می باشد) که دارای یک نقطۀ پایانی می باشد و در جهت دیگر تا ابد ادامه می یابد. اگر این نقطۀ پایانی \(K\) باشد و از میان نقطۀ \(S\) عبور کند و تا ابد ادامه یابد، این نیم خط را، نیم خطِ \(KS\) می نامید و آن را به شکل \(\overrightarrow{KS}\) می نویسید. شکل 2-2 را ببینید.
اولین حرف همواره نقطۀ پایانیِ نیم خط را نشان می دهد. به عنوان مثال، \(\overrightarrow{AB}\) می تواند \(\overrightarrow{AC}\) نیز نامیده شود، زیرا در هر دو صورت، شما از نقطۀ \(A\) آغاز می کنید و تا ابد ادامه می دهید و در این میان از نقاط \(B\) و \(C\) نیز عبور می کنید. با این وجود، \(\overrightarrow{BC}\) یک نیم خط دیگر است.
دو نیم خط با نقطۀ پایانی یکسان یک زاویه را شکل می دهند. هر نیم خط ضلعی از آن زاویه می باشد، و نقطۀ پایانی مشترک، رأس (vertex) این زاویه است، شما می توانید یک زاویه را صرفاً با رأس آن یا با سه نقطه نامگذاری کنید (ابتدا، یک نقطه بر روی یکی از نیم خطها، سپس رأس، و سپس یک نقطه بر روی آن یکی نیم خطِ تشکیل دهندۀ زاویه).
شکل 3-2 را بررسی کنید. نیم خطهای \(\overrightarrow{PQ}\) و \(\overrightarrow{PR}\) اضلاع یک زاویه هستند، و نقطۀ \(P\) رأس آن زاویه می باشد. شما می توانید این زاویه را \(\angle{P}\) ، \(\angle{RPQ}\) ، یا \(\angle{QPR}\) بنامید. همچنین می توانید زاویه ها را با اعداد نیز نامگذاری کنید، مانند زاویه ای که در سمت راست تصویر می بینید که آن را \(\angle{4}\) نامیده ایم. این عدد صرفاً روش دیگری برای نامگذاری زاویه می باشد و هیچ ارتباطی به اندازۀ آن زاویه ندارد.
همچنین زاویۀ موجود در سمت راست تصویر بخش درونی (interior) و بخش بیرونی (exterior) در یک زاویه را نشان می دهد.
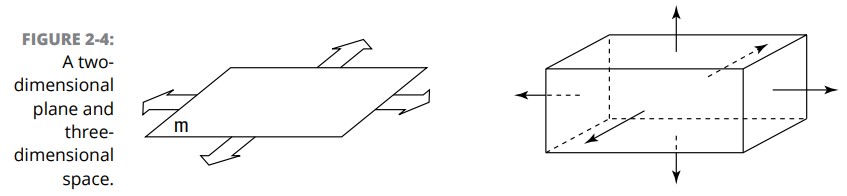
یک صفحه مانند یک ورق کاغذ کاملاً مسطح می باشد با این استثناء که ابداً هیچ ضخامتی ندارد و در تمامی جهتها تا ابد ادامه می یابد. شما می توانید بگویید که صفحه بی نهایت باریک است و بی نهایت طول و بی نهایت عرض دارد. از آنجا که یک صفحه فقط دارای طول و عرض است و ارتفاع ندارد، دو بعدی (two-dimensional) می باشد. صفحه ها با یک حرف کوچک مورب نامگذاری می شوند، گاهی اوقات هم صفحات را با نام یک شکل (به عنوان مثال یک مستطیل) که در آن صفحه قرار گرفته است، نامگذاری می کنند. شکل 4-2 صفحۀ \(m\) را که در چهار جهت تا ابد ادامه می یابد را به شما نشان می دهد.
فضای سه بعدی همه جا هست ـــ تمامی فضا در تمامی جهتها. ابتدا، یک نقشۀ بی نهایت بزرگ را تصور کنید که تا ابد به سمت شمال، جنوب، شرق، و غرب ادامه می یابد. این یک صفحۀ دو بعدی است. سپس برای اینکه از این نقشه یک فضای سه بعدی بدست آوریم، با بالا و پایین رفتن تا ابد، بُعد سومی را به آن بیفزایید. برای ترسیم یک فضای سه بعدی هیچ روش خوبی وجود ندارد (شکل 4-2 بهترین تلاش من را به شما نشان می دهد). برخلاف یک جعبه (مکعب)، یک فضای سه بعدی دارای شکل یا حاشیه نیست.
از آنجا که یک فضای سه بعدی تمامی فضای جهان را می گیرد، به نوعی متضاد نقطه می باشد، که به هیچ وجه هیچ فضایی را نمی گیرد. اما از سوی دیگر، از آن جهت که هم فضای سه بعدی و هم نقطه، تعریفشان مشکل می باشد، با هم شباهت دارند، زیرا هر دوی اینها به صورت کامل بدون ویژگی هایی هستند.

تعاریف پایه هندسه
مطالعۀ هندسه با تعریف پنج شیء سادۀ هندسی آغاز می گردد: نقطه (point)، خط (line)، پاره خط (segment)، نیم خط (ray)، و زاویه (angle). و من دو تعریف دیگر نیز به آن اضافه می کنم: صفحه (plane) و فضای سه بعدی (\(\text{3-D space}\)). در مجموع، این جملات شما را از بدون بُعد به سه بُعد می برند.
در اینجا تعاریف پاره خط، نیم خط، زاویه، صفحه، و فضای سه بعدی را می بینید، همینطور مفاهیم بدون تعریف نقطه و خط را نیز خواهید شناخت (دو مفهوم نقطه و خط از لحاظ فنی بدون تعریف و یا غیرقابل تعریف می باشند).
نقطه (Point)
یک نقطه همانند یک لکه خیلی کوچک است، با این تفاوت که در حقیقت هیچ اندازه ای ندارد؛ یا می توانید اینطور بگویید که نقطه بی نهایت کوچک است. اساساً ابعاد یک نقطه صفر می باشد، بدون هیچ ارتفاع، طول، یا عرض. اما شما آن را مانند یک لکه ترسیم می کنید. شما نقطه ها را با حروف بزرگ نشان می دهید، مانند نقطه های \(A\)، \(D\)، و \(T\) در شکل 1-2 .
خط (Line)
خط شبیه یک سیم نازک و راست است (اگرچه در حقیقت بی نهایت نازک است ـــ یا بهتر است بگوییم، به هیچ وجه عرضی ندارد). خطها دارای طول می باشند، بنابراین آنها دارای یک بعد (one-dimensional) هستند. یادتان باشد که یک خط در هر دوسمت آن تا ابد پیش می رود، به همین دلیل هم هست که از یک فلش دوسرِ کوچک برای نشان دادن خط \(\overleftrightarrow{AB}\) استفاده می کنید. (این نماد به صورت خط \(AB\) خوانده می شود).
شکل 1-2 را دوباره بررسی کنید. خطها معمولاً با استفاده از هر دو نقطه ای بر روی آنها نامگذاری می شوند، ترتیب قرار گیری این حروف در نامگذاری خط حائز اهمیت نیست. بنابراین خط \(\overleftrightarrow{MQ}\) با خط \(\overleftrightarrow{QM}\) یکسان می باشند، خط \(\overleftrightarrow{MN}\) همان خط \(\overleftrightarrow{NM}\) است، و \(\overleftrightarrow{QN}\) همان \(\overleftrightarrow{NQ}\) می باشد. گاهی اوقات، خطها را با یک حرف کوچک و تنها و با حروف کج نامگذاری می کنند، مانند خطهای \(f\) و \(g\) .
پاره خط (Line segment)
یک پاره خط، بخشی از یک خط است که دارای دو نقطۀ پایانی می باشد. شکل 1-2 را دوباره ببینید. اگر یک پاره خط از \(P\) به \(R\) برود، شما آن را پاره خط \(PR\) می نامید و به شکل \(\overline{PR}\) می نویسید. شما همچنین می توانید ترتیب حروف را تعویض کنید و آن را \(\overline{RP}\) بنامید. همچنین پاره خطها می توانند درون خطها ظاهر شوند، مانند \(\overline{MN}\) .
نکته: یک جفت حروف بدون یک خط در بالای آنها به معنای طول یک پاره خط می باشد، به عنوان مثال، \(PR\) به معنای طول \(\overline{PR}\) می باشد.

نیم خط (Ray)
نیم خط بخشی از یک خط می باشد (به نوعی نصف یک خط می باشد) که دارای یک نقطۀ پایانی می باشد و در جهت دیگر تا ابد ادامه می یابد. اگر این نقطۀ پایانی \(K\) باشد و از میان نقطۀ \(S\) عبور کند و تا ابد ادامه یابد، این نیم خط را، نیم خطِ \(KS\) می نامید و آن را به شکل \(\overrightarrow{KS}\) می نویسید. شکل 2-2 را ببینید.
اولین حرف همواره نقطۀ پایانیِ نیم خط را نشان می دهد. به عنوان مثال، \(\overrightarrow{AB}\) می تواند \(\overrightarrow{AC}\) نیز نامیده شود، زیرا در هر دو صورت، شما از نقطۀ \(A\) آغاز می کنید و تا ابد ادامه می دهید و در این میان از نقاط \(B\) و \(C\) نیز عبور می کنید. با این وجود، \(\overrightarrow{BC}\) یک نیم خط دیگر است.
زاویه (Angle)
دو نیم خط با نقطۀ پایانی یکسان یک زاویه را شکل می دهند. هر نیم خط ضلعی از آن زاویه می باشد، و نقطۀ پایانی مشترک، رأس (vertex) این زاویه است، شما می توانید یک زاویه را صرفاً با رأس آن یا با سه نقطه نامگذاری کنید (ابتدا، یک نقطه بر روی یکی از نیم خطها، سپس رأس، و سپس یک نقطه بر روی آن یکی نیم خطِ تشکیل دهندۀ زاویه).
شکل 3-2 را بررسی کنید. نیم خطهای \(\overrightarrow{PQ}\) و \(\overrightarrow{PR}\) اضلاع یک زاویه هستند، و نقطۀ \(P\) رأس آن زاویه می باشد. شما می توانید این زاویه را \(\angle{P}\) ، \(\angle{RPQ}\) ، یا \(\angle{QPR}\) بنامید. همچنین می توانید زاویه ها را با اعداد نیز نامگذاری کنید، مانند زاویه ای که در سمت راست تصویر می بینید که آن را \(\angle{4}\) نامیده ایم. این عدد صرفاً روش دیگری برای نامگذاری زاویه می باشد و هیچ ارتباطی به اندازۀ آن زاویه ندارد.
همچنین زاویۀ موجود در سمت راست تصویر بخش درونی (interior) و بخش بیرونی (exterior) در یک زاویه را نشان می دهد.

صفحه (Plane)
یک صفحه مانند یک ورق کاغذ کاملاً مسطح می باشد با این استثناء که ابداً هیچ ضخامتی ندارد و در تمامی جهتها تا ابد ادامه می یابد. شما می توانید بگویید که صفحه بی نهایت باریک است و بی نهایت طول و بی نهایت عرض دارد. از آنجا که یک صفحه فقط دارای طول و عرض است و ارتفاع ندارد، دو بعدی (two-dimensional) می باشد. صفحه ها با یک حرف کوچک مورب نامگذاری می شوند، گاهی اوقات هم صفحات را با نام یک شکل (به عنوان مثال یک مستطیل) که در آن صفحه قرار گرفته است، نامگذاری می کنند. شکل 4-2 صفحۀ \(m\) را که در چهار جهت تا ابد ادامه می یابد را به شما نشان می دهد.
فضای سه بعدی (\(\text{3-D space}\))
فضای سه بعدی همه جا هست ـــ تمامی فضا در تمامی جهتها. ابتدا، یک نقشۀ بی نهایت بزرگ را تصور کنید که تا ابد به سمت شمال، جنوب، شرق، و غرب ادامه می یابد. این یک صفحۀ دو بعدی است. سپس برای اینکه از این نقشه یک فضای سه بعدی بدست آوریم، با بالا و پایین رفتن تا ابد، بُعد سومی را به آن بیفزایید. برای ترسیم یک فضای سه بعدی هیچ روش خوبی وجود ندارد (شکل 4-2 بهترین تلاش من را به شما نشان می دهد). برخلاف یک جعبه (مکعب)، یک فضای سه بعدی دارای شکل یا حاشیه نیست.
از آنجا که یک فضای سه بعدی تمامی فضای جهان را می گیرد، به نوعی متضاد نقطه می باشد، که به هیچ وجه هیچ فضایی را نمی گیرد. اما از سوی دیگر، از آن جهت که هم فضای سه بعدی و هم نقطه، تعریفشان مشکل می باشد، با هم شباهت دارند، زیرا هر دوی اینها به صورت کامل بدون ویژگی هایی هستند.

یادتان باشد: در اینجا چیزی اندکی عجیب و غریب در مورد روشی که اشیاء در نمودارهای هندسی نشان داده می شوند، داریم: حتی با وجود اینکه، خطها، پاره خطها، نیم خطها، و به همین ترتیب، در یک نمودار ظاهر نمی شوند، آنها هنوز هم به نوعی وجود دارند ـــ مشروط بر اینکه شما بدانید آنها را کجا ترسیم کنید. به عنوان مثال، شکل 1-2 شامل یک پاره خط، \(\overline{PD}\)، است، که از \(P\) تا \(D\) می رود و دارای نقاط پایانی در \(P\) و \(D\) می باشد ـــ حتی اگر شما نتوانید آنها را ببینید. (می دانم که این ممکن است اندکی عجیب به نظر برسد، اما این ایده یکی از قوانین این بازی است. نگران نباشید.)
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: