خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
خطهای متعامد بر صفحات
تمامی هندسۀ ارائه شده در فصلهای قبل از این شامل شکلهای دو بعدی بودند. در این فصل، شما برای اولین بار شکل های هندسی و اثبات های سه بعدی را بررسی می کنید، شانس این را پیدا می کنید که خطها و صفحات، و چگونگی تعامل آنها با یکدیگر را در یک فضای سه بعدی بررسی کنید. اما برخلاف مکعب ها، کره ها، و استوانه های سه بعدی، که شما در زندگی روزمره می بینید، چیزهای سه بعدی ارائه شده در این فصل، به چیزهای مسطح دو بعدی که در فصل های قبل مشاهده کردید، ساده سازی شده اند، که در یک فضای سه بعدی روی پا ایستاده اند.

یک صفحه (plane) صرفاً یک چیز مسطح است، مانند یک تکه کاغذ، با این استثناء که بی نهایت باریک می باشد و در تمامی جهات تا ابد ادامه می یابد (فصل 2 چیزهای بیشتری در مورد صفحات به شما می گوید). در این بخش، شما درخواهید یافت اینکه یک خط بر یک صفحه عمود باشد، به چه معناست و چگونه از این تعامد در یک اثبات دو ستونی استفاده کنید.
در اثبات های دو ستونی، شما از قضیه و تعریف پیشین به دلایل مختلفی استفاده می کنید:
اطمینان حاصل کنید که شما درک کرده اید که یک خط باید بر روی دو خط متفاوت در یک صفحه عمود باشد، تا شما بتوانید نتیجه گیری کنید آن خط بر آن صفحه عمود می باشد. (این دو خط در آن صفحه همواره در فوت (foot) خطی که بر صفحه عمود می باشد، همدیگر را قطع می کنند.) تعامد بر یک خط در یک صفحه کافی نمی باشد. در اینجا دلیل آن را داریم: فرض کنید شما یک حرف بزرگ \(L\) دارید که از جنس پلاستیک ساخته شده است، و شما آن را روی یک میز به صورت سرپا نگه داشته اید. هنگامی که آن حرف \(L\) به سمت بالا اشاره می کند، بخش عمودی حرف \(L\) بر روی آن میز عمود می باشد. حالا اندکی \(L\) را یک وری کنید (پایۀ آن را روی میز نگهدارید)، بنابراین بالای \(L\) هم اکنون در یک زاویۀ غیر \(90^{\circ}\) قرار دارد. قطعاً بالای این \(L\) هنوز بر روی انتهای آن عمود می باشد (که یک خط است که در این صفحه قرار دارد)، اما بالای این \(L\) دیگر بر آن میز عمود نمی باشد. از اینرو، یک خط که از یک صفحه بیرون زده است می تواند یک زاویۀ قائمه را با یک خط در آن صفحه ایجاد کند و با این وجود بر خود آن صفحه عمود نباشد.
آیا برای چند مسأله آماده اید؟ بفرمایید این هم مسالۀ اول:
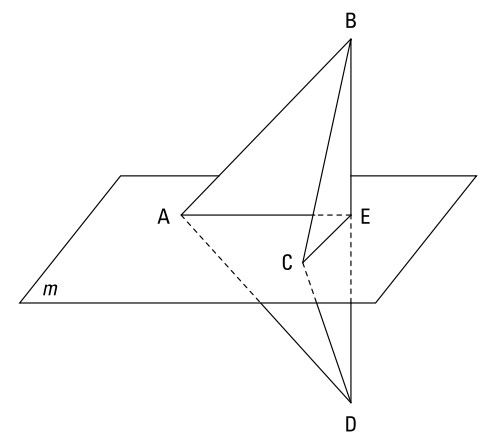
داده ها:
\(\overline{BD} \bot m\)
\(\angle{EBC} \cong \angle{EDC}\)
اثبات کنید:
\(\overline{AB} \cong \overline{AD}\)

توجه داشته باشید: برای اینکه اثبات کنید \(\triangle{BEC} \cong \triangle{DEC}\) (در گزارۀ 7)، دو روش خوب دیگر هم وجود دارد. هر دوی این روش ها از خاصیت بازتابی بر روی \(\overline{EC}\) استفاده می کنند، و یکی از این روشها با AAS و دیگری با HLR مسأله را تمام می کنند. هر سۀ این روشها تعداد مراحل یکسانی دارند. من از روش نمایش داده شده به این دلیل استفاده کرده ام که بر روی اهمیت قضیۀ اگر زوایا، سپس اضلاع، تاکید کنم (دلیل 6).
در اثبات بعدی هم از تعریف و هم از قضیۀ تعامد خط-صفحه، استفاده شده است (برای کمک گرفتن در مورد اینکه چگونه تصمیم بگیرید از کدام یکی از اینها در کجاها استفاده کنید، توضیحات ارائه شده در لیست بالا را دوباره بخوانید).
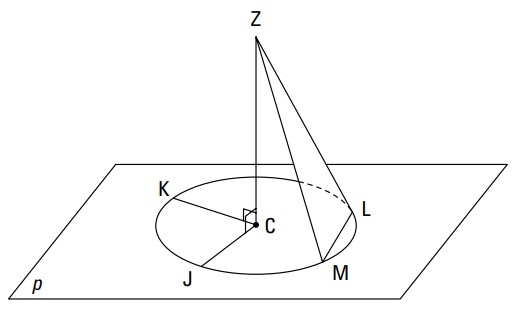
داده ها:
دایرۀ \(C\)
\(\angle{JCZ}\) یک زاویۀ قائمه می باشد
\(\angle{KCZ}\) یک زاویۀ قائمه می باشد
اثبات کنید:
\(\angle{ZLM} \cong \angle{ZML}\)
در اینجا اثبات رسمی را می بینید:


خطهای متعامد بر صفحات
یک صفحه (plane) صرفاً یک چیز مسطح است، مانند یک تکه کاغذ، با این استثناء که بی نهایت باریک می باشد و در تمامی جهات تا ابد ادامه می یابد (فصل 2 چیزهای بیشتری در مورد صفحات به شما می گوید). در این بخش، شما درخواهید یافت اینکه یک خط بر یک صفحه عمود باشد، به چه معناست و چگونه از این تعامد در یک اثبات دو ستونی استفاده کنید.
تعریف تعامد خط-صفحه (Line-Plane perpendicularity definition): گفتن اینکه یک خط بر یک صفحه عمود می باشد، بدین معناست که آن خط بر هر خطی در آن صفحه که از فوت (foot) آن می گذرد، عمود می باشد. (یک فوت (foot) نقطه ای است که یک خط یک صفحه را قطع می کند.)
قضیۀ تعامد خط-صفحه (Line-Plane perpendicularity theorem): اگر یک خط بر دو خط متفاوت دیگر که در یک صفحه قرار گرفته اند و از فوت (foot) آن خط عبور می کنند، عمود باشد، آن گاه، آن خط بر آن صفحه عمود می باشد.
در اثبات های دو ستونی، شما از قضیه و تعریف پیشین به دلایل مختلفی استفاده می کنید:
-
استفاده از این تعریف: هنگامی که شما می دانید که یک خط بر یک صفحه عمود می باشد و می خواهید نشان دهید که این خط بر روی یک خط که در آن صفحه قرار گرفته است، عمود می باشد (به طور خلاصه، اگر \(\bot\) بر یک صفحه، سپس \(\bot\) بر خط).
-
استفاده از این قضیه: هنگامی که شما می دانید که یک خط بر دو خط در یک صفحه عمود می باشد و می خواهید نشان دهید که آن خط بر خود آن صفحه عمود می باشد (به طور خلاصه، اگر \(\bot\) بر روی دو خط، سپس \(\bot\) صفحه). توجه داشته باشید که این تقریباً معکوس فرآیند مورد اول در این لیست می باشد.
اطمینان حاصل کنید که شما درک کرده اید که یک خط باید بر روی دو خط متفاوت در یک صفحه عمود باشد، تا شما بتوانید نتیجه گیری کنید آن خط بر آن صفحه عمود می باشد. (این دو خط در آن صفحه همواره در فوت (foot) خطی که بر صفحه عمود می باشد، همدیگر را قطع می کنند.) تعامد بر یک خط در یک صفحه کافی نمی باشد. در اینجا دلیل آن را داریم: فرض کنید شما یک حرف بزرگ \(L\) دارید که از جنس پلاستیک ساخته شده است، و شما آن را روی یک میز به صورت سرپا نگه داشته اید. هنگامی که آن حرف \(L\) به سمت بالا اشاره می کند، بخش عمودی حرف \(L\) بر روی آن میز عمود می باشد. حالا اندکی \(L\) را یک وری کنید (پایۀ آن را روی میز نگهدارید)، بنابراین بالای \(L\) هم اکنون در یک زاویۀ غیر \(90^{\circ}\) قرار دارد. قطعاً بالای این \(L\) هنوز بر روی انتهای آن عمود می باشد (که یک خط است که در این صفحه قرار دارد)، اما بالای این \(L\) دیگر بر آن میز عمود نمی باشد. از اینرو، یک خط که از یک صفحه بیرون زده است می تواند یک زاویۀ قائمه را با یک خط در آن صفحه ایجاد کند و با این وجود بر خود آن صفحه عمود نباشد.
آیا برای چند مسأله آماده اید؟ بفرمایید این هم مسالۀ اول:

داده ها:
\(\overline{BD} \bot m\)
\(\angle{EBC} \cong \angle{EDC}\)
اثبات کنید:
\(\overline{AB} \cong \overline{AD}\)

ترجمۀ شکل:
-
\(\overline{BD} \bot m\)
داده.
-
\(\overline{BD} \bot \overline{EC}\)
اگر یک خط بر یک صفحه عمود باشد، سپس بر هر خطی در آن صفحه که از فوت (foot) آن عبور کند، عمود می باشد (تعریف تعامد خط بر روی صفحه).
-
\(\angle{BEC}\) یک زاویۀ قائمه می باشد
\(\angle{DEC}\) یک زاویۀ قائمه می باشد
تعریف خطهای متعامد.
-
\(\angle{BEC} \cong \angle{DEC}\)
تمامی زوایای قائمه با یکدیگر همنهشتند.
-
\(\angle{EBC} \cong \angle{EDC}\)
داده.
-
\(\overline{BC} \cong \overline{DC}\)
اگر زوایا، سپس اضلاع.
-
\(\triangle{BEC} \cong \triangle{DEC}\)
اصل AAS (خطهای 4،5،6).
-
\(\overline{BE} \cong \overline{DE}\)
CPCTC
-
\(\overline{AE} \cong \overline{AE}\)
خاصیت بازتابی.
-
\(\overline{BD} \bot \overline{AE}\)
اگر یک خط بر یک صفحه عمود باشد، سپس بر روی هر خطی در آن صفحه که از فوت آن می گذرد، عمود می باشد.
-
\(\angle{BEA}\) یک زاویۀ قائمه می باشد
\(\angle{DEA}\) یک زاویۀ قائمه می باشد
تعریف خطهای متعامد.
-
\(\angle{BEA} \cong \angle{DEA}\)
تمامی زوایای قائمه با هم همنهشتند.
-
\(\triangle{ABE} \cong \triangle{ADE}\)
اصل SAS (خطهای 8،12،9).
-
\(\overline{AB} \cong \overline{AD}\)
CPCTC
توجه داشته باشید: برای اینکه اثبات کنید \(\triangle{BEC} \cong \triangle{DEC}\) (در گزارۀ 7)، دو روش خوب دیگر هم وجود دارد. هر دوی این روش ها از خاصیت بازتابی بر روی \(\overline{EC}\) استفاده می کنند، و یکی از این روشها با AAS و دیگری با HLR مسأله را تمام می کنند. هر سۀ این روشها تعداد مراحل یکسانی دارند. من از روش نمایش داده شده به این دلیل استفاده کرده ام که بر روی اهمیت قضیۀ اگر زوایا، سپس اضلاع، تاکید کنم (دلیل 6).
در اثبات بعدی هم از تعریف و هم از قضیۀ تعامد خط-صفحه، استفاده شده است (برای کمک گرفتن در مورد اینکه چگونه تصمیم بگیرید از کدام یکی از اینها در کجاها استفاده کنید، توضیحات ارائه شده در لیست بالا را دوباره بخوانید).

داده ها:
دایرۀ \(C\)
\(\angle{JCZ}\) یک زاویۀ قائمه می باشد
\(\angle{KCZ}\) یک زاویۀ قائمه می باشد
اثبات کنید:
\(\angle{ZLM} \cong \angle{ZML}\)
در اینجا اثبات رسمی را می بینید:

ترجمۀ شکل:
-
دایرۀ \(C\)
\(\angle{JCZ}\) یک زاویۀ قائمه می باشد
\(\angle{KCZ}\) یک زاویۀ قائمه می باشد
داده.
-
\(\overline{ZC} \bot \overline{JC}\)
\(\overline{ZC} \bot \overline{KC}\)
تعریف خطهای متعامد.
-
\(\overline{ZC} \bot p\)
اگر یک خط بر دو خط که در یک صفحه قرار دارند و از فوت (foot) آن عبور می کنند، عمود باشد، سپس بر آن صفحه عمود می باشد.
-
ترسیم \(\overline{CL}\)
ترسیم \(\overline{CM}\)
دو خط یک پاره خط را تعیین می کنند.
-
\(\overline{CL} \cong \overline{CM}\)
همۀ شعاع های یک دایره همنهشت می باشند.
-
\(\overline{ZC} \bot \overline{CL}\)
\(\overline{ZC} \bot \overline{CM}\)
اگر یک خط بر یک صفحه عمود باشد، سپس بر روی هر خطی از آن صفحه که از فوت آن عبور کند، عمود می باشد.
-
\(\angle{ZCL}\) یک زاویۀ قائمه می باشد
\(\angle{ZCM}\) یک زاویۀ قائمه می باشد
تعریف خطهای متعامد.
-
\(\angle{ZCL} \cong \angle{ZCM}\)
تمامی زوایای قائمه با یکدیگر همنهشت می باشند.
-
\(\overline{ZC} \cong \overline{ZC}\)
خاصیت بازتابی.
-
\(\triangle{ZCL} \cong \triangle{ZCM}\)
اصل SAS (خطهای 5،8،9).
-
\(\overline{ZL} \cong \overline{ZM}\)
CPCTC
-
\(\angle{ZLM} \cong \angle{ZML}\)
اگر اضلاع، سپس زوایا.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: