قبل از هر چیز به تعریف کره می پردازیم. کُره مجموعۀ تمام نقاط در یک فضای سه بعدی می باشد که از یک نقطۀ ثابت، فاصلۀ یکسانی داشته باشند، که به آن مرکز کره گفته می شود. (به زبان ساده، کره یک توپ است.) شعاع یک کره از مرکز آن تا سطح آن می باشد.






یک توپ با مسالۀ کرۀ زیر دارید: حجم و مساحت رویۀ یک توپ بسکتبال درون یک باکس (box)، این باکس مکعب مربع (cube) می باشد، در صورتی که مسات رویۀ این باکس \(486\) اینچ مربع (square inches) باشد، چقدر می باشد؟

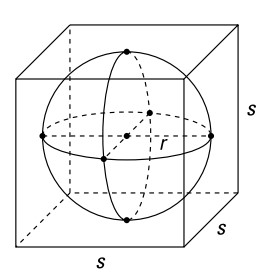
یک مکعب مربع (cube) (یا هر شکل باکس معمولی دیگر) یک نوع خاص از منشور (prism) می باشد، اما شما به فرمول فانتزی منشور نیاز ندارید، زیرا مساحت رویۀ یک مکعب مربع به سادگی از شش مربع همنشهت تشکیل شده است. اگر یکی از یال های این مکعب مربع را \(s\) بنامید، بنابراین مساحت هر کناره برابر با \(s^2\) خواهد بود. مکعب مربع دارای شش وجه می باشد، پس مساحت رویۀ آن برابر با \(6s^2\) خواهد بود. این را با مساحت رویۀ داده شده یعنی \(486\) اینچ مربع (square inches) یکی قرار دهید و آن را برای یافتن \(s\) حل کنید:
$$
6s^2=486 \\
s^2=81 \\
s =9 \text{ inches}
$$
بنابراین، یال این مکعب مربع برابر با \(9\) می باشد، و از آنجا که این توپ بسکتبال با این باکس عرض یکسانی دارد، قطر توپ نیز برابر با \(9\) اینچ خواهد بود؛ شعاع آن نصف آن یعنی \(4.5\) اینچ می شود. اکنون می توانید با جایگذازی \(4.5\) در فرمول های کره، این مسأله را به پایان برسانید:
$$
\text{Vol}_{\text{Sphere}}={4\over3}\pi r^3 \\
={4\over3}\pi 4.5^3 \\
=121.5\pi\\
\approx 381.7 \text{ cubic inches}
$$
حالا در اینجا پاسخ مساحت رویه را داریم:
$$
\text{SA}_{\text{Sphere}}=4 \pi r^2 \\
=4 \pi 4.5^2 \\
=81 \pi \\
\approx 254.5 \text{ square inches}
$$
در صورتی که کنجکاو باشید، این کُره در اندازۀ واقعی یک توپ بسکتبال رسمی در لیگ NBA می باشد. برای به پایان رساندن این فصل، در اینجا یک سوال بی ربط به موضوع برای شما داریم (قبل از مشاهدۀ پاسخ سعی کنید حدس خودتان را بزنید). اکنون که می دانید قطر یک توپ بسکتبال برابر با \(9\) اینچ می باشد، فکر می کنید قطر حلقۀ بسکتبال چقدر باشد؟ پاسخ سورپرایز کننده اینست که قطر حلقۀ بسکتبال کاملاً دوبرابر قطر توپ بسکتبال یعنی \(18\) اینچ می باشد!