خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
ده مفهوم کلیدی در ریاضی که نباید نادیده بگیرید
خود ریاضی یک مفهوم بزرگ است، و از مفاهیم کوچک بسیاری پرشده است که هیچ کس، هر چقدر هم در طولانی مدت ریاضی خوانده باشد، احتمالاً نمی تواند همه آنها را درک کند.

اما درون این همه، برخی مفاهیم خیلی پخش شده اند که از دیدگاه فروتنانه من، آنها تالار مشاهیر ریاضی را ساخته اند. هر کدام از این ایده ها نه تنها ریاضی، بلکه شیوه تفکر مردم نسبت به جهان را تغییر داده اند. دانستن آنها می تواند دنیای شما را تغییر بدهد، یا حداقل دید وسیعتری در مورد ریاضی به شما می دهد.
خوب، در اینجا لیست ده تا از مفاهیم مهم ریاضی از دید بنده را می بینید.
یک مجموعه (set) یک کلکسیون از اشیاء می باشد. این اشیاء که عناصر (elements) مجموعه نامیده می شوند، می توانند محسوس (کفش، گربۀ وحشی، مردم، شکلات های ژله ای، و ...) و یا نامشهود (شخصیت های داستانی، ایده ها، اعداد و مواردی ازاین قبیل) باشند.
مجموعه ها یک روش ساده و انعطاف پذیر برای سازماندهی جهان هستند که شما می توانید تمامی ریاضی را از منظر آنها تعریف کنید. اینکه ریاضی دانان چگونه این کار را انجام می دهند خیلی پیچیده است، اما یک درک اولیه از مجموعه ها سخت نمی باشد و بخشی از بیشتر آموزش های آکادمیک ریاضی است. برای کسب اطلاعات بیشتر در مورد نظریه مجموعه ها (set theory) فصل 20 را ببینید، و برای مشاهده برخی از مجموعه های اعداد حائز اهمیت، فصل 25 را ببینید.
یک عدد اول (prime number) هر عدد شمارشی (counting number) می باشد که دقیقاً دو مقسوم علیه دارد، 1 و خود آن عدد. در اینجا لیست ده عدد اول را می بینید:
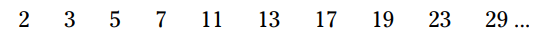
اعداد اول تا ابد ادامه پیدا می کنند، یعنی این لیست بی نهایت می باشد.
فراتر از آن، اعداد اول از جنبه دیگری نیز حائز اهمیت هستند، و آن اینکه آنها عناصری هستند که سازنده تمامی اعداد دیگر می باشند. هر عدد شمارشی (counting number) که بزرگتر از 1 باشد، مهم هم نیست که چقدر عدد بزرگی باشد، می تواند به شکل یک حاصلضرب انحصاری از اعداد اول نوشته شود.
انحصاری بودن فاکتورهای اول هر عدد (prime factors) آنقدر حائز اهمیت بوده است که برایش نامی بگذارند: قضیه اساسی حساب (the Fundamental Theorem of Arithmetic). برای کسب اطلاعات بیشتر در مورد اعداد اول، فصل 1 و 7 را ببینید.
صفر ممکن است شبیه یک "هیچ چی" بزرگ باشد، اما در واقع یکی از بزرگترین اختراعات تمامی دورانها می باشد. مثل همۀ اختراعات دیگر، صفر وجود نداشت، تا اینکه کسی به آن اندیشید. یونانیان و رومی ها، که اطلاعات زیادی در مورد ریاضی و منطق داشتند، چیزی در مورد صفر نمی دانستند. سیستم اعدادی که آنها استفاده می کردند، راهی برای بیان صفر نداشت، برای مثال، اگر شما سه درخت زیتون داشته باشید و یک همسایۀ عصبانی هر سه آنها را قطع کند، چند درخت باقی می ماند.
مفهوم صفر به عنوان یک عدد، به صورت مستقل در چندین مکان مختلف به وجود آمد. در آمریکای جنوبی، سیستم اعدادی که توسط مایاها (Mayans) مورد استفاده قرار می گرفت شامل نمادی برای صفر بود. و سیستم هندو-عربی که امروزه در سراسر جهان استفاده می شود از روی سیستم پیشین عربی توسعه یافته است که در آن از صفر به عنوان نگهدارندۀ جا (placeholder) استفاده می شده است. (برای کسب اطلاعات بیشتر در مورد استفاده از صفر به عنوان نگهدارنده جا، فصل 2 را ببینید.)
در واقع، صفر هیچ چیز نیست، بلکه به سادگی فقط روشی برای نمایش دادن هیچ چیز (nothing) به شکل ریاضی می باشد. و خودش واقعاً چیزی می باشد.
عدد پی که آن را با نماد π نشان می دهند، یک حرف الفبای یونانی می باشد که نشان دهنده نسبت بین محیط دایره و قطر آن می باشد. (برای مشاهده جزئیات بیشتر در مورد دایره، فصل 16 را ببینید). در اینجا مقدار تقریبی π را می بینید:
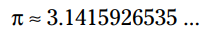
اگرچه π صرفاً یک عدد می باشد - یا به لحاظ جبری یک ثابت می باشد - به چندین دلیل، مهم می باشد:
تقریباً هر شخصی می پندارد علامت برابری (=) برای همیشه آنجا بوده است. این علامت آنقدر در ریاضی رایج است که عملاً به آن بی توجهی می شود. اما واقعیت اینست که علامت برابری که تقریباً همه جا دیده می شود این ایده را تقویت می کند که مفهوم برابری (equality) - این مفهوم یعنی یک چیز از لحاظ ریاضی مشابه چیز دیگری می باشد - یکی از مهمترین مفاهیم ریاضی است که تاکنون ایجاد شده است.
یک بیانیه ریاضی (mathematical statement) با یک علامت برابری یک معادله (equation) می باشد. علامت برابری دو عبارت ریاضی (mathematical expressions) را که مقدار یکسانی دارند، به یکدیگر مرتبط می کند. قدرت ریاضی در این ارتباط نهفته است. به همین دلیل هم هست که تقریباً هر چیزی در ریاضی درگیر با معادلات می باشد. عبارت ها به خودی خود، در سودمند بودن محدود می باشند. علامت برابری یک روش قدرتمند برای مرتبط کردن عبارتها فراهم می کند، که به دانشمندان اجازه می دهد ایده ها را با روش های جدیدی به یکدیگر مرتبط کنند.
برای مثال، برای هزاران سال، انرژی (energy) و ماده (matter) به عنوان دو چیز جداگانه و غیر مرتبط شناخته می شدند. فرمول معروف انیشتین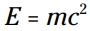 عبارتی را که نماینده انرژی است با عبارت دیگری که نمایانگر ماده است، مرتبط کرد. نتیجۀ آن یک دیدگاه رادیکال تغییر یافته نسبت به جهان می باشد.
عبارتی را که نماینده انرژی است با عبارت دیگری که نمایانگر ماده است، مرتبط کرد. نتیجۀ آن یک دیدگاه رادیکال تغییر یافته نسبت به جهان می باشد.
برای جزئیات بیشتر در مورد اینکه مفاهیم برابری و تعادل چه نقشی را در جبر ایفا می کنند، فصل 22 را مرور کنید.
گراف دکارتی - همچنین سیستم مختصات دکارتی (Cartesian coordinate system) نیز نامیده می شود - یک نام فانتزی برای یک گراف خوب و قدیمی می باشد که در فصل 17 معرفی کردم. این گراف توسط فیلسوف و ریاضیدان فرانسوی رنه دکارت (René Descartes) اختراع شد.
چه چیزی در مورد گراف دکارتی خیلی خاص است؟ قبل از اینکه این گراف اختراع شود، برای قرنها جبر و هندسه به عنوان دو ناحیه جداگانه و غیرمرتبط در ریاضی مورد مطالعه قرار می گرفتند. جبر به طور انحصاری مطالعه معادلات می باشد (بخش 5 کتاب را ببینید)، و هندسه منحصراً مطالعه شکلها در سطح یا در فضا می باشد (فصل 16 را ببینید).
اختراع گراف توسط دکارت، جبر و هندسه را گرد هم آورد. نتیجه هندسه تحلیلی (analytic geometry) شد، یک ریاضیات جدید که نه تنها دو علم باستانی جبر و هندسه را ادغام کرده است، در عین حال وضوح بیشتری برای هر دوی آنها به وجود آورده است. در حال حاضر، شما می توانید راه حل هایی برای معادلات ترسیم کنید که در آنها متغیرهای x و y به شکل نقطه، خط، دایره و سایر شکلهای هندسی بر روی گراف وجود دارند.
یک تابع (function) یک دستگاه ریاضی می باشد که یک عدد را به عنوان ورودی (input) دریافت می کند و دقیقاً یک عدد دیگر را به عنوان خروجی (output) برمی گرداند. تابع، به نوعی شبیه یک دستگاه مخلوط کن می باشد چرا که آنچیزی را که از آن بیرون می کشید بستگی به چیزی دارد که در آن قرار می دهید: اگر در آن بستنی قرار بدهید، یک میلک شیک از آن دریافت می کنید. اگر در آن میوه قرار بدهید، یک اسموتی میوه دریافت می کنید. هنگامی که تلفن همراهتان را در آن قرار می دهید، یک تلفن به شدت آسیب دیده دریافت خواهید کرد.
فرض کنید من یک تابع با نام PlusOne اختراع کرده ام که عدد 1 را به هر عددی اضافه می کند. بنابراین اگر عدد 2 را در آن قرار بدهید، عدد خروجی 3 خواهد بود:
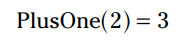
به طرز مشابهی، اگر ورودی این تابع عدد 100 باشد، خروجی آن عدد 101 خواهد بود:
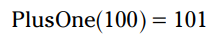
همانطور که می بینید، هرگاه که عدد زوجی را در این تابع قرار دهید، خروجی تابع PlusOne یک عدد فرد خواهد بود. و این اتفاق در مورد هر عدد زوجی خواهد افتاد. بنابراین، این تابع بین مجموعه اعداد زوج و مجموعه اعداد فرد تناظر برقرار می کند.
این فرآیند ممکن است ساده به نظر آید، و البته در هنگام کار با مجموعه ها، همین سادگی توابع به آنها قدرت می دهد. توابع به ریاضیدانان - و گروههای دیگری همچون برنامه نویسان کامپیوترها، آمارگیران، زیست شناسان، اقتصاد دانان، و روانشناسان - امکان می دهد تا یک دنیای پیچیده را با یک روش ریاضی درک کنند.
هرچه در جبر پیش بروید، خواهید دید توابع نقش های خیلی زیادی را ایفا خواهند کرد. فعلاً فقط یادتان باشد که یک تابع یک ورودی را می گیرد و یک خروجی به شما می دهد. برای درک عمیقتر موضوع توابع، کتاب Algebra For Dummies را بخوانید.
کلمه بی نهایت (infinity) نشان دهنده قدرتی عظیم است. نماد بی نهایت (∞) می باشد. بی نهایت چقدر بزرگ است؟ این یک پرسش رایج است: اگر تمامی شن ها در تمامی ساحل های جهان را بشمارید، و این کار را برای تک تک سیارات کهکشان انجام بدهید، وقتی که شمارش شما تمام شد، از آنچیزی که الآن هستید به بی نهایت نزدیکتر نخواهید شد. بله قربان، تا این حد بزرگ است!!!
در واقع، بی نهایت خودش یک عدد نیست. بی نهایت، فراتر از هر نوع دسته بندی اندازه ها یا اعداد می باشد، بی نهایت مفهوم پایان ناپذیری دارد. و با این حال، ریاضیدانان تا حد زیادی بی نهایت را اهلی کرده اند.
خط اعداد (number line) مدت بسیاری است که همین اطراف بوده است، و یکی از اولین ابزارهای بصری است که معلم ها برای آموزش اعداد به بچه ها مورد استفاده قرار می دهند. هر نقطه بر روی خط اعداد نماینده یک عدد می باشد. خوب، اوکی، این خیلی بدیهی به نظر می رسد، اما عجیب است که بگویم، این مفهوم برای هزاران سال به خوبی درک نشده بود.
فیلسوف یونانی زنون (Zeno) این مسأله را مطرح کرده که پارادوکس زنون (Zeno’s Paradox) نامیده می شود: برای راه رفتن از این سمت اتاق به آن سمت اتاق، شما ابتدا باید نصف این مسیر را طی کنید، یعنی 1/2 مسیر. سپس شما باید نصفی از باقیمانده مسیر را طی کنید، یعنی 1/4 مسیر. بعد از آن شما باید نصفه باقیمانده مسیر را طی کنید، یعنی 1/8 مسیر. این الگو تا ابد ادامه پیدا می کند:
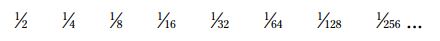
با این حساب، شما هرگز به سمت دیگر اتاق نخواهید رسید.
بدیهی است که در دنیای واقعی، شما هر وقت بخواهید می توانید به سادگی از این سمت اتاق به آن سمتش بروید. اما از نقطه نظر ریاضی، پارادوکس زنون و سایر پارادوکس های مشابه آن، برای حدود 2000 سال بدون پاسخ باقی ماندند.
مشکل اساسی این بود: تمامی کسرهایی که در دنباله قبلی لیست شده اند در خط اعداد بین 0 و 1 می باشند. و تعداد بی نهایت از این کسرها وجود دارد. اما چطور می شود در یک فضای محدود، تعداد بی نهایت عدد وجود داشته باشد؟
اعداد موهومی (imaginary numbers) یک مجموعه از اعداد هستند که در خط اعداد حقیقی یافت نمی شوند. اگر این ایده به نظر باور کردنی نمی رسد - پس این اعداد کجا هستند؟ - نگران نباشید: برای هزاران سال ریاضیدانان این اعداد را باور نداشتند. اما کاربردهای دنیای واقعی در الکترونیک، فیزیک ذرات، و ناحیه های بسیار دیگری از علوم، این شکاکان را به باورمندان تبدیل کرد.
برای اطلاعات بیشتر در مورد اعداد موهومی فصل 25 را ببینید.

اما درون این همه، برخی مفاهیم خیلی پخش شده اند که از دیدگاه فروتنانه من، آنها تالار مشاهیر ریاضی را ساخته اند. هر کدام از این ایده ها نه تنها ریاضی، بلکه شیوه تفکر مردم نسبت به جهان را تغییر داده اند. دانستن آنها می تواند دنیای شما را تغییر بدهد، یا حداقل دید وسیعتری در مورد ریاضی به شما می دهد.
خوب، در اینجا لیست ده تا از مفاهیم مهم ریاضی از دید بنده را می بینید.
مجموعه ها (Sets)
یک مجموعه (set) یک کلکسیون از اشیاء می باشد. این اشیاء که عناصر (elements) مجموعه نامیده می شوند، می توانند محسوس (کفش، گربۀ وحشی، مردم، شکلات های ژله ای، و ...) و یا نامشهود (شخصیت های داستانی، ایده ها، اعداد و مواردی ازاین قبیل) باشند.
مجموعه ها یک روش ساده و انعطاف پذیر برای سازماندهی جهان هستند که شما می توانید تمامی ریاضی را از منظر آنها تعریف کنید. اینکه ریاضی دانان چگونه این کار را انجام می دهند خیلی پیچیده است، اما یک درک اولیه از مجموعه ها سخت نمی باشد و بخشی از بیشتر آموزش های آکادمیک ریاضی است. برای کسب اطلاعات بیشتر در مورد نظریه مجموعه ها (set theory) فصل 20 را ببینید، و برای مشاهده برخی از مجموعه های اعداد حائز اهمیت، فصل 25 را ببینید.
اعداد اول (Prime Numbers)
یک عدد اول (prime number) هر عدد شمارشی (counting number) می باشد که دقیقاً دو مقسوم علیه دارد، 1 و خود آن عدد. در اینجا لیست ده عدد اول را می بینید:
اعداد اول تا ابد ادامه پیدا می کنند، یعنی این لیست بی نهایت می باشد.
فراتر از آن، اعداد اول از جنبه دیگری نیز حائز اهمیت هستند، و آن اینکه آنها عناصری هستند که سازنده تمامی اعداد دیگر می باشند. هر عدد شمارشی (counting number) که بزرگتر از 1 باشد، مهم هم نیست که چقدر عدد بزرگی باشد، می تواند به شکل یک حاصلضرب انحصاری از اعداد اول نوشته شود.
انحصاری بودن فاکتورهای اول هر عدد (prime factors) آنقدر حائز اهمیت بوده است که برایش نامی بگذارند: قضیه اساسی حساب (the Fundamental Theorem of Arithmetic). برای کسب اطلاعات بیشتر در مورد اعداد اول، فصل 1 و 7 را ببینید.
صفر (Zero)
صفر ممکن است شبیه یک "هیچ چی" بزرگ باشد، اما در واقع یکی از بزرگترین اختراعات تمامی دورانها می باشد. مثل همۀ اختراعات دیگر، صفر وجود نداشت، تا اینکه کسی به آن اندیشید. یونانیان و رومی ها، که اطلاعات زیادی در مورد ریاضی و منطق داشتند، چیزی در مورد صفر نمی دانستند. سیستم اعدادی که آنها استفاده می کردند، راهی برای بیان صفر نداشت، برای مثال، اگر شما سه درخت زیتون داشته باشید و یک همسایۀ عصبانی هر سه آنها را قطع کند، چند درخت باقی می ماند.
مفهوم صفر به عنوان یک عدد، به صورت مستقل در چندین مکان مختلف به وجود آمد. در آمریکای جنوبی، سیستم اعدادی که توسط مایاها (Mayans) مورد استفاده قرار می گرفت شامل نمادی برای صفر بود. و سیستم هندو-عربی که امروزه در سراسر جهان استفاده می شود از روی سیستم پیشین عربی توسعه یافته است که در آن از صفر به عنوان نگهدارندۀ جا (placeholder) استفاده می شده است. (برای کسب اطلاعات بیشتر در مورد استفاده از صفر به عنوان نگهدارنده جا، فصل 2 را ببینید.)
در واقع، صفر هیچ چیز نیست، بلکه به سادگی فقط روشی برای نمایش دادن هیچ چیز (nothing) به شکل ریاضی می باشد. و خودش واقعاً چیزی می باشد.
عدد پی (π)
عدد پی که آن را با نماد π نشان می دهند، یک حرف الفبای یونانی می باشد که نشان دهنده نسبت بین محیط دایره و قطر آن می باشد. (برای مشاهده جزئیات بیشتر در مورد دایره، فصل 16 را ببینید). در اینجا مقدار تقریبی π را می بینید:
اگرچه π صرفاً یک عدد می باشد - یا به لحاظ جبری یک ثابت می باشد - به چندین دلیل، مهم می باشد:
-
علم هندسه (Geometry)، بدون آن به این شکل فعلی نمی بود. دایره ها یک از پایه ای ترین شکلها در هندسه می باشند، شما برای اندازه گیری مساحت و محیط یک دایره به عدد π نیاز دارید. بنابراین اگر بیگانگان با بشقاب پرنده هایشان در مزرعه ذرت شما فرود بیایند و بخواهید دایره های حاصل از محل فرود را اندازه گیری کنید، و یا اگر فقط بخواهید مساحت میز آشپزخانه گردتان را بدانید، عدد پی (π) یک ابزار سودمند در دستان شما خواهد بود.
-
پی یک عدد گنگ (irrational number) می باشد، به این معنا که هیچ کسری وجود ندارد که دقیقاً برابر با آن باشد. فراتر از آن، π یک عدد متعالی (transcendental number) می باشد، به این معنا که هرگز در یک معادله چند جمله ای (polynomial equation) مقدار x برابر با آن نخواهد بود. بنابراین، با اینکه π برای یک عملیات ساده (اندازه گیری دایره) به وجود آمده است، شامل یک پیچیدگی عمیق است که اعدادی همچون 0 یا 1 یا 1- یا 1/2 و حتی 2√ فاقد آن می باشند. (برای کسب اطلاعات بیشتر در مورد اعداد گنگ و اعداد متعالی، فصل 25 را ببینید.)
-
پی در همه جای ریاضی هست. عدد پی به طور مداوم در جاهایی که انتظارش را ندارید ظاهر می گردد. یک مثال مثلثاث (trigonometry) می باشد (مطالعۀ مثلث ها). بدیهی است که مثلث ها دایره نمی باشند، اما مثلثاث از دایره ها برای اندازه گیری زاویه ها استفاده می کند، و شما نمی توانید بدون اصابت کردن با π یک قطب نما را نوسان بدهید.
علامتهای برابری (Equal Signs) و معادلات (Equations)
تقریباً هر شخصی می پندارد علامت برابری (=) برای همیشه آنجا بوده است. این علامت آنقدر در ریاضی رایج است که عملاً به آن بی توجهی می شود. اما واقعیت اینست که علامت برابری که تقریباً همه جا دیده می شود این ایده را تقویت می کند که مفهوم برابری (equality) - این مفهوم یعنی یک چیز از لحاظ ریاضی مشابه چیز دیگری می باشد - یکی از مهمترین مفاهیم ریاضی است که تاکنون ایجاد شده است.
یک بیانیه ریاضی (mathematical statement) با یک علامت برابری یک معادله (equation) می باشد. علامت برابری دو عبارت ریاضی (mathematical expressions) را که مقدار یکسانی دارند، به یکدیگر مرتبط می کند. قدرت ریاضی در این ارتباط نهفته است. به همین دلیل هم هست که تقریباً هر چیزی در ریاضی درگیر با معادلات می باشد. عبارت ها به خودی خود، در سودمند بودن محدود می باشند. علامت برابری یک روش قدرتمند برای مرتبط کردن عبارتها فراهم می کند، که به دانشمندان اجازه می دهد ایده ها را با روش های جدیدی به یکدیگر مرتبط کنند.
برای مثال، برای هزاران سال، انرژی (energy) و ماده (matter) به عنوان دو چیز جداگانه و غیر مرتبط شناخته می شدند. فرمول معروف انیشتین
برای جزئیات بیشتر در مورد اینکه مفاهیم برابری و تعادل چه نقشی را در جبر ایفا می کنند، فصل 22 را مرور کنید.
گراف دکارتی (Cartesian Graph)
گراف دکارتی - همچنین سیستم مختصات دکارتی (Cartesian coordinate system) نیز نامیده می شود - یک نام فانتزی برای یک گراف خوب و قدیمی می باشد که در فصل 17 معرفی کردم. این گراف توسط فیلسوف و ریاضیدان فرانسوی رنه دکارت (René Descartes) اختراع شد.
چه چیزی در مورد گراف دکارتی خیلی خاص است؟ قبل از اینکه این گراف اختراع شود، برای قرنها جبر و هندسه به عنوان دو ناحیه جداگانه و غیرمرتبط در ریاضی مورد مطالعه قرار می گرفتند. جبر به طور انحصاری مطالعه معادلات می باشد (بخش 5 کتاب را ببینید)، و هندسه منحصراً مطالعه شکلها در سطح یا در فضا می باشد (فصل 16 را ببینید).
اختراع گراف توسط دکارت، جبر و هندسه را گرد هم آورد. نتیجه هندسه تحلیلی (analytic geometry) شد، یک ریاضیات جدید که نه تنها دو علم باستانی جبر و هندسه را ادغام کرده است، در عین حال وضوح بیشتری برای هر دوی آنها به وجود آورده است. در حال حاضر، شما می توانید راه حل هایی برای معادلات ترسیم کنید که در آنها متغیرهای x و y به شکل نقطه، خط، دایره و سایر شکلهای هندسی بر روی گراف وجود دارند.
توابع (Functions)
یک تابع (function) یک دستگاه ریاضی می باشد که یک عدد را به عنوان ورودی (input) دریافت می کند و دقیقاً یک عدد دیگر را به عنوان خروجی (output) برمی گرداند. تابع، به نوعی شبیه یک دستگاه مخلوط کن می باشد چرا که آنچیزی را که از آن بیرون می کشید بستگی به چیزی دارد که در آن قرار می دهید: اگر در آن بستنی قرار بدهید، یک میلک شیک از آن دریافت می کنید. اگر در آن میوه قرار بدهید، یک اسموتی میوه دریافت می کنید. هنگامی که تلفن همراهتان را در آن قرار می دهید، یک تلفن به شدت آسیب دیده دریافت خواهید کرد.
فرض کنید من یک تابع با نام PlusOne اختراع کرده ام که عدد 1 را به هر عددی اضافه می کند. بنابراین اگر عدد 2 را در آن قرار بدهید، عدد خروجی 3 خواهد بود:
به طرز مشابهی، اگر ورودی این تابع عدد 100 باشد، خروجی آن عدد 101 خواهد بود:
همانطور که می بینید، هرگاه که عدد زوجی را در این تابع قرار دهید، خروجی تابع PlusOne یک عدد فرد خواهد بود. و این اتفاق در مورد هر عدد زوجی خواهد افتاد. بنابراین، این تابع بین مجموعه اعداد زوج و مجموعه اعداد فرد تناظر برقرار می کند.
این فرآیند ممکن است ساده به نظر آید، و البته در هنگام کار با مجموعه ها، همین سادگی توابع به آنها قدرت می دهد. توابع به ریاضیدانان - و گروههای دیگری همچون برنامه نویسان کامپیوترها، آمارگیران، زیست شناسان، اقتصاد دانان، و روانشناسان - امکان می دهد تا یک دنیای پیچیده را با یک روش ریاضی درک کنند.
هرچه در جبر پیش بروید، خواهید دید توابع نقش های خیلی زیادی را ایفا خواهند کرد. فعلاً فقط یادتان باشد که یک تابع یک ورودی را می گیرد و یک خروجی به شما می دهد. برای درک عمیقتر موضوع توابع، کتاب Algebra For Dummies را بخوانید.
یادداشت مترجم: خبر خوب برای شما عزیزان اینکه، ترجمه کتاب پیش رو تا چند روز آینده خاتمه می یابد و به همین زودی ترجمه کتاب "جبر برای احمق ها" (Algebra For Dummies) را آغاز می کنم و طبق روال سابق به صورت رایگان از طریق سایت خوش آموز در اختیار شما عزیزان قرار خواهد گرفت.
بی نهایت (Infinite)
کلمه بی نهایت (infinity) نشان دهنده قدرتی عظیم است. نماد بی نهایت (∞) می باشد. بی نهایت چقدر بزرگ است؟ این یک پرسش رایج است: اگر تمامی شن ها در تمامی ساحل های جهان را بشمارید، و این کار را برای تک تک سیارات کهکشان انجام بدهید، وقتی که شمارش شما تمام شد، از آنچیزی که الآن هستید به بی نهایت نزدیکتر نخواهید شد. بله قربان، تا این حد بزرگ است!!!
در واقع، بی نهایت خودش یک عدد نیست. بی نهایت، فراتر از هر نوع دسته بندی اندازه ها یا اعداد می باشد، بی نهایت مفهوم پایان ناپذیری دارد. و با این حال، ریاضیدانان تا حد زیادی بی نهایت را اهلی کرده اند.
خط اعداد حقیقی (Real Number Line)
خط اعداد (number line) مدت بسیاری است که همین اطراف بوده است، و یکی از اولین ابزارهای بصری است که معلم ها برای آموزش اعداد به بچه ها مورد استفاده قرار می دهند. هر نقطه بر روی خط اعداد نماینده یک عدد می باشد. خوب، اوکی، این خیلی بدیهی به نظر می رسد، اما عجیب است که بگویم، این مفهوم برای هزاران سال به خوبی درک نشده بود.
فیلسوف یونانی زنون (Zeno) این مسأله را مطرح کرده که پارادوکس زنون (Zeno’s Paradox) نامیده می شود: برای راه رفتن از این سمت اتاق به آن سمت اتاق، شما ابتدا باید نصف این مسیر را طی کنید، یعنی 1/2 مسیر. سپس شما باید نصفی از باقیمانده مسیر را طی کنید، یعنی 1/4 مسیر. بعد از آن شما باید نصفه باقیمانده مسیر را طی کنید، یعنی 1/8 مسیر. این الگو تا ابد ادامه پیدا می کند:
با این حساب، شما هرگز به سمت دیگر اتاق نخواهید رسید.
بدیهی است که در دنیای واقعی، شما هر وقت بخواهید می توانید به سادگی از این سمت اتاق به آن سمتش بروید. اما از نقطه نظر ریاضی، پارادوکس زنون و سایر پارادوکس های مشابه آن، برای حدود 2000 سال بدون پاسخ باقی ماندند.
مشکل اساسی این بود: تمامی کسرهایی که در دنباله قبلی لیست شده اند در خط اعداد بین 0 و 1 می باشند. و تعداد بی نهایت از این کسرها وجود دارد. اما چطور می شود در یک فضای محدود، تعداد بی نهایت عدد وجود داشته باشد؟
نکات فنی: ریاضیدانان قرن نوزدهم - آگوستین کوشی (Augustin Cauchy)، ریچارد ددکیند (Richard Dedekind)، کارل وایرشتراس (Karl Weierstrass)، و مهمتر از همه جورج کانتور (Georg Cantor) - این پارادوکس را حل کرده اند. نتیجه آن "تجزیه و تحلیل واقعی" (real analysis) شده است، ریاضیات پیشرفته ای که به خط اعداد حقیقی (Real Number Line) می پردازد.
عدد موهومی i
اعداد موهومی (imaginary numbers) یک مجموعه از اعداد هستند که در خط اعداد حقیقی یافت نمی شوند. اگر این ایده به نظر باور کردنی نمی رسد - پس این اعداد کجا هستند؟ - نگران نباشید: برای هزاران سال ریاضیدانان این اعداد را باور نداشتند. اما کاربردهای دنیای واقعی در الکترونیک، فیزیک ذرات، و ناحیه های بسیار دیگری از علوم، این شکاکان را به باورمندان تبدیل کرد.
برای اطلاعات بیشتر در مورد اعداد موهومی فصل 25 را ببینید.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: