خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
ضرب و تقسیم توان ها، توان منفی، توانِ توان
شما می توانید عبارتهای توان دار بسیاری را بدون اینکه مجبور باشید شکل آنها را به اعداد بزرگ یا کوچکی که نمایانگر آنها هستند، تغییر بدهید، در یکدیگر ضرب کنید. تنها الزام در اینجا اینست که پایه های (bases) عبارتهای توان دار با یکدیگر برابر باشند. پاسخ نیز یک عبارت زیبا و شسته و رفته توان دار خواهد بود.

شما می توانید عبارتهای زیر را ضرب کنید:
برای ضرب توان های دارای پایه یکسان، توان ها را با یکدیگر جمع کنید:
مثال: در اینجا چند مثال از پیدا کردن حاصلضرب اعداد با جمع زدن توان های آنها را می بینید:

اغلب، با عبارتهای جبری (algebraic expressions) برخورد می کنید که یک رشته کامل از فاکتورها می باشند، شما می خواهید تا حد ممکن آن عبارت را ساده کنید. هنگامی که در یک عبارت دارای توان، بیش از یک پایه باشد، شما پایه های یکسان را با یکدیگر ترکیب می کنید، مقادیر را پیدا می کنید، و سپس همه آنها را با یکدیگر می نویسید.
مثال: در اینجا چگونگی ساده کردن عبارتهایی را که در ادامه آمده اند، می بینید:
شما می توانید عبارتهای توان دار را، در صورتیکه دارای پایه های یکسان باشند، تقسیم کنید و پاسخ تقسیم را نیز به صورت یک عبارت توان دار بنویسید. تقسیم معکوس عملیات ضرب می باشد، بنابراین این معنادار است که، از آنجایی که در ضرب اعداد دارای پایه یکسان، توان ها را با هم جمع می زدید، در تقسیم اعداد دارای پایه های یکسان، توان ها را از یکدیگر تفریق کنید. به حد کافی ساده است!
مثال: در اینجا چند مثال از ساده کردن عبارات با تقسیم، می بینید:
نیاز هست بیشتر بگویم؟ خوب، بله، خیلی چیزهای بیشتر برای گفتن است - مخصوصاً در مورد هیچی (nothing). من لازم می بینم در مورد توان هیچی - بهتر است بگویم 0 - چیزهایی را به عرضتان برسانم.
اگر x3 برابر است با x.x.x، پس x0 چه معنایی می دهد؟ خوب، به معنای 0 مرتبه x نمی باشد، پس پاسخ 0 نیست. x نماینده عددی ناشناس و حقیقی است، اعداد حقیقی را می توان به توان 0 رساند - به شرطی که پایه آنها 0 نباشد. برای درک چگونگی کارکرد آن، از قانون زیر برای تقسیم های عبارتهای توان دار که شامل 0 می باشند استفاده کنید.
وضعیتی را در نظر بگیرید که با استفاده از قوانین تقسیم عبارتهای توان دار، مشغول تقسیم 24 بر 24 هستید. قانون به شما می گوید اگر پایه ها یکسان باشند، توان ها را به ترتیب از هم تفریق کنید. با انجام این کار متوجه می شوید که پاسخ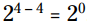 می شود. اما
می شود. اما 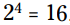 ، بنابراین
، بنابراین 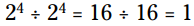 . این یعنی
. این یعنی 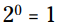 . این قانون همیشه - به جز پایه 0 - برقرار است.
. این قانون همیشه - به جز پایه 0 - برقرار است.
مثال: در اینجا چند مثال از ساده سازی عبارات داریم، در آنها از این قانون که اگر یک عدد حقیقی به توان 0 برسد، نتیجه 1 خواهد شد، استفاده کنید:
توان های منفی مخلوقات کوچک خوبی هستند. آنها معنای خیلی خاصی دارند و باید با دقت به آنها رسیدگی شود، اما آنها خیلی راحت هستند.
شما می توانید از یک توان منفی (negative exponent) برای نوشتن یک کسر استفاده کنید، بدون اینکه کسری را بنویسید! استفاده از توان های منفی روشی برای ترکیب عبارتهای دارای پایه یکسان می باشد، خواه اینکه فاکتورهای متفاوت در صورت یا در مخرج کسر باشند. همچنین روشی برای تبدیل مسأله های تقسیم به مسأله های ضرب می باشد.
توان های منفی روشی برای نوشتن توان کسرها یا اعداد اعشاری، بدون استفاده از کسر یا عدد اعشاری، می باشند. برای مثال، به جای نوشتن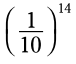 شما می توانید بنویسید:
شما می توانید بنویسید: 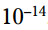 .
.
مثال: در اینجا چند مثال از تبدیل اعداد دارای توان منفی به کسرهای دارای توان مثبت می بینید:
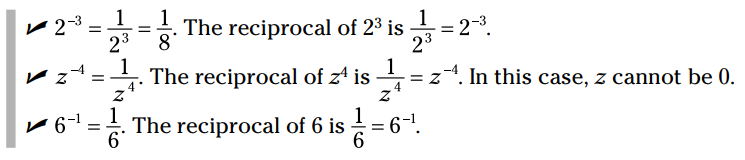
اما اگر با یک توان منفی در مخرج کسر کار را آغاز کنید، چه می شود؟ در آن صورت چه اتفاقی خواهد افتاد؟ به کسر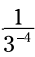 نگاه کنید. اگر شما مخرج را به شکل یک کسر بنویسید، خواهید داشت
نگاه کنید. اگر شما مخرج را به شکل یک کسر بنویسید، خواهید داشت 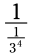 . سپس، کسر مرکب (complex fraction) - کسری که داخل آن کسر دیگری باشد - را به یک مسأله تقسیم تبدیل می کنیم:
. سپس، کسر مرکب (complex fraction) - کسری که داخل آن کسر دیگری باشد - را به یک مسأله تقسیم تبدیل می کنیم: 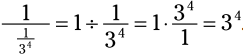 . (اگر در این زمینه نیاز به یاد آوری دارید، فصل 3 را مرور کنید.) بنابراین، برای ساده سازی یک کسر که در مخرجش عددی منفی می باشد، می توانید آن را معکوس کنید:
. (اگر در این زمینه نیاز به یاد آوری دارید، فصل 3 را مرور کنید.) بنابراین، برای ساده سازی یک کسر که در مخرجش عددی منفی می باشد، می توانید آن را معکوس کنید: 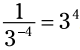 .
.
مثال: در اینجا چند مثال از ساده سازی کسرها با روش خلاص شدن از شر توان های منفی می بینید:
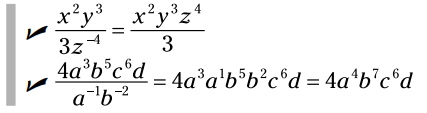
از آنجایی که توان ها نمادهایی برای ضرب های تکراری می باشند، یک روش برای نوشتن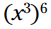 این می باشد:
این می باشد: 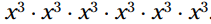 . با استفاده از قوانین ضرب اعداد توان دار که شما فقط توان ها را با یکدیگر جمع می زدید، خواهید داشت:
. با استفاده از قوانین ضرب اعداد توان دار که شما فقط توان ها را با یکدیگر جمع می زدید، خواهید داشت: 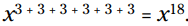 . آیا اگر قانون محاسبه توانِ توان تنها ضرب توان ها در یکدیگر می بود، عالی نمی شد؟ پس خوش به حال شما!
. آیا اگر قانون محاسبه توانِ توان تنها ضرب توان ها در یکدیگر می بود، عالی نمی شد؟ پس خوش به حال شما!
مثال: در اینجا چند مثال از ساده سازی عبارات با استفاده از قانون به توان رساندن توان داریم:

شما می توانید عبارتهای زیر را ضرب کنید:
24 · 26 a5 · a8اما شما نمی توانید عبارت زیر را ضرب نمایید:
36 · 47زیرا پایه ها یکسان نیستند.
برای ضرب توان های دارای پایه یکسان، توان ها را با یکدیگر جمع کنید:
xa · xb = xa + b
مثال: در اینجا چند مثال از پیدا کردن حاصلضرب اعداد با جمع زدن توان های آنها را می بینید:
اغلب، با عبارتهای جبری (algebraic expressions) برخورد می کنید که یک رشته کامل از فاکتورها می باشند، شما می خواهید تا حد ممکن آن عبارت را ساده کنید. هنگامی که در یک عبارت دارای توان، بیش از یک پایه باشد، شما پایه های یکسان را با یکدیگر ترکیب می کنید، مقادیر را پیدا می کنید، و سپس همه آنها را با یکدیگر می نویسید.
مثال: در اینجا چگونگی ساده کردن عبارتهایی را که در ادامه آمده اند، می بینید:
-
در اینجا دو فاکتوری که دارای پایه 3 می باشند با یکدیگر ترکیب می شوند، همچنین دو فاکتور دارای پایه 2 نیز با یکدیگر ترکیب می شوند.
-
عدد 4 یک ضریب (coefficient) می باشد، که قبل از بقیه فاکتورها نوشته شده است.
یادتان باشد: اگر توانی نشان داده نشده باشد، مانند y، فرض شما این باشد که توان 1 است. در مثال قبلی، شما دیدید که فاکتور y به شکل y1 نوشته شد، بنابراین توان آن که 1 می باشد هم اکنون قابل جمع زدن با سایر توان ها می باشد.
نکات فنی: شما می توانید در هنگام ضرب اعداد دارای پایه های یکسان توان های آنها را با هم جمع بزنید. اما در مورد ضرب اعداد دارای توان های یکسان چطور؟ قانون اینست که:
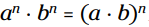 بنابراین اگر شما داشته باشید:
بنابراین اگر شما داشته باشید: 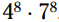 ، می توانید آن را به شکل زیر ساده کنید:
، می توانید آن را به شکل زیر ساده کنید:
 شما ترجیح خواهید داد که عبارت ساده شده را به شکل توانی از عدد 28 نشان بدهید، زیرا عدد واقعی بسیار بزرگ می باشد!
شما ترجیح خواهید داد که عبارت ساده شده را به شکل توانی از عدد 28 نشان بدهید، زیرا عدد واقعی بسیار بزرگ می باشد!
تقسیم توان ها
شما می توانید عبارتهای توان دار را، در صورتیکه دارای پایه های یکسان باشند، تقسیم کنید و پاسخ تقسیم را نیز به صورت یک عبارت توان دار بنویسید. تقسیم معکوس عملیات ضرب می باشد، بنابراین این معنادار است که، از آنجایی که در ضرب اعداد دارای پایه یکسان، توان ها را با هم جمع می زدید، در تقسیم اعداد دارای پایه های یکسان، توان ها را از یکدیگر تفریق کنید. به حد کافی ساده است!
قوانین جبر: برای تقسیم توان های دارای پایه یکسان، توان ها را تفریق کنید:
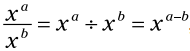 در عبارت بالا x می تواند هر عدد حقیقی به جز 0 باشد. (یادتان باشد، شما نمی توانید بر 0 تقسیم کنید.)
در عبارت بالا x می تواند هر عدد حقیقی به جز 0 باشد. (یادتان باشد، شما نمی توانید بر 0 تقسیم کنید.)
مثال: در اینجا چند مثال از ساده کردن عبارات با تقسیم، می بینید:
-
این مقادیر توانی مسأله زیر را نشان می دهند:
1,024 ÷ 16 = 64
بسیار ساده تر است که پاسخ را به شکل یک عدد توان دار بنویسیم.
-
متغیرها نماینده اعداد هستند، بنابراین، نوشتن این عبارت به صورت بدون توانی به شکل زیر خواهد بود:
با خط زدن فاکتورهای مشترک آنچه باقی می ماند
می باشد.
نیاز هست بیشتر بگویم؟ خوب، بله، خیلی چیزهای بیشتر برای گفتن است - مخصوصاً در مورد هیچی (nothing). من لازم می بینم در مورد توان هیچی - بهتر است بگویم 0 - چیزهایی را به عرضتان برسانم.
توان صفر
اگر x3 برابر است با x.x.x، پس x0 چه معنایی می دهد؟ خوب، به معنای 0 مرتبه x نمی باشد، پس پاسخ 0 نیست. x نماینده عددی ناشناس و حقیقی است، اعداد حقیقی را می توان به توان 0 رساند - به شرطی که پایه آنها 0 نباشد. برای درک چگونگی کارکرد آن، از قانون زیر برای تقسیم های عبارتهای توان دار که شامل 0 می باشند استفاده کنید.
قوانین جبر: هر عددی به توان 0 برابر است با 1، به شرطیکه پایه توان خودش 0 نباشد. به عبارت دیگر:
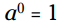 مشروط بر اینکه
مشروط بر اینکه 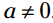 .
.
وضعیتی را در نظر بگیرید که با استفاده از قوانین تقسیم عبارتهای توان دار، مشغول تقسیم 24 بر 24 هستید. قانون به شما می گوید اگر پایه ها یکسان باشند، توان ها را به ترتیب از هم تفریق کنید. با انجام این کار متوجه می شوید که پاسخ
مثال: در اینجا چند مثال از ساده سازی عبارات داریم، در آنها از این قانون که اگر یک عدد حقیقی به توان 0 برسد، نتیجه 1 خواهد شد، استفاده کنید:
-
-
در اینجا x و z در نهایت به توان 0 می رسند، بنابراین آن فاکتورها تبدیل به 1 می شوند. نه x و نه z هیچکدام برابر با 0 نیستند.
-
کار با توان های منفی
توان های منفی مخلوقات کوچک خوبی هستند. آنها معنای خیلی خاصی دارند و باید با دقت به آنها رسیدگی شود، اما آنها خیلی راحت هستند.
شما می توانید از یک توان منفی (negative exponent) برای نوشتن یک کسر استفاده کنید، بدون اینکه کسری را بنویسید! استفاده از توان های منفی روشی برای ترکیب عبارتهای دارای پایه یکسان می باشد، خواه اینکه فاکتورهای متفاوت در صورت یا در مخرج کسر باشند. همچنین روشی برای تبدیل مسأله های تقسیم به مسأله های ضرب می باشد.
توان های منفی روشی برای نوشتن توان کسرها یا اعداد اعشاری، بدون استفاده از کسر یا عدد اعشاری، می باشند. برای مثال، به جای نوشتن
یادتان باشد: متقابل یک عدد (reciprocal)، معکوس ضربی آن عدد می باشد. حاصلضرب یک عدد و متقابل آن برابر با 1 می باشد.
قوانین جبر: متقابل 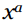 برابر با
برابر با 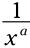 می باشد، که می تواند به صورت
می باشد، که می تواند به صورت 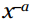 نوشته شود. متغیر x می تواند هر عدد حقیقی به جز 0 باشد، و متغیر a نیز می تواند هر عدد حقیقی باشد. همچنین برای خلاص شدن از شر توان منفی می توانید آن را به این شکل بنویسید:
نوشته شود. متغیر x می تواند هر عدد حقیقی به جز 0 باشد، و متغیر a نیز می تواند هر عدد حقیقی باشد. همچنین برای خلاص شدن از شر توان منفی می توانید آن را به این شکل بنویسید: 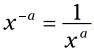 .
.
مثال: در اینجا چند مثال از تبدیل اعداد دارای توان منفی به کسرهای دارای توان مثبت می بینید:
اما اگر با یک توان منفی در مخرج کسر کار را آغاز کنید، چه می شود؟ در آن صورت چه اتفاقی خواهد افتاد؟ به کسر
مثال: در اینجا چند مثال از ساده سازی کسرها با روش خلاص شدن از شر توان های منفی می بینید:
توانِ توان
از آنجایی که توان ها نمادهایی برای ضرب های تکراری می باشند، یک روش برای نوشتن
قوانین جبر: برای به توان رساندن یک توان، از این فرمول استفاده کنید:
(xn)m = xnmبه عبارت دیگر، هنگامی که یک عبارت کامل xn به توان m ام برسد، توان جدید x با ضرب n در m مشخص می شود.
مثال: در اینجا چند مثال از ساده سازی عبارات با استفاده از قانون به توان رساندن توان داریم:
-
: ابتدا توان ها را در یکدیگر ضرب کنید، سپس حاصلضرب بدست آمده را به شکلی بازنویسی کنید که توان منفی تبدیل به توان مثبت گردد.
-
-
-
: هر فاکتور در داخل پرانتز به توان بیرون پرانتز می رسد.
-
توجه کنید که ترتیب عملیات در اینجا مشاهده می شود. ابتدا عبارات داخل پرانتز را به توانهایشان می رسانید. سپس دو عبارت را در یکدیگر ضرب می کنید. این مثال ضرب توان ها (به توان رساندن یک توان)، و جمع زدن توان ها (ضرب توان های دارای پایه یکسان) را به شما نشان می دهد. قوانین ترتیب عملیات شامل همه عبارات می شوند حتی اگر شما توان های منفی داشته باشید.
-
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (3 دیدگاه)
دیدگاه خود را ثبت کنید: