خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
مقدمات عملیات کسرها

برای جمع، تفریق، یا مقایسه کسرها، شما نیاز به کسرهایی دارید که به تعداد تکه های مساوی تقسیم شده باشند. به عبارت دیگر، مخرج های (denominators) آنها باید برابر باشند.

مخرج های مشترک (common denominators) - اعداد یکسان در مخرج کسرها - برای عملیات جمع، تفریق، و مقایسه کسرها ضروری می باشند. کسرهای برابر با 1 که با دقت انتخاب شده اند برای ایجاد مخرج های مشترک مورد استفاده قرار می گیرند، زیرا ضرب کسرها در عدد 1 مقدار آنها را تغییر نمی دهد.
برای پیدا کردن یک مخرج مشترک (common denominator) برای دو کسر و نوشتن کسرهای برابر، این مراحل را دنبال کنید:
در اینجا چگونگی پیدا کردن یک مخرج مشترک برای دو کسر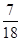 و
و 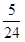 را می بینید.
را می بینید.
در اینجا چگونگی پیدا کردن کوچکترین مخرج مشترک برای دو کسر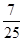 و
و 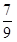 را می بینید:
را می بینید:
همانطور که در ادامه این فصل خواهید دید، ضرب و تقسیم کسرهای ناسره مشکلتر از ضرب و تقسیم کسرهای سره نمی باشد. اگرچه، باز هم همانطور که در ادامه فصل خواهید دید، در صورتی که نتیجه نهایی را به صورت یک عدد مختلط (mixed number) بنویسید، درک آن ساده تر می باشد. همچنین، اگر با یک عدد مختلط آغاز کنید و نیاز داشته باشید که کسرناسره معادل آن را ببینید چه کار باید کنید؟ پاسخ این سوال را در همینجا به شما می دهم.
برای تبدیل یک کسرناسره به یک عددمختلط، صورت کسر را بر مخرج آن تقسیم کنید. قسمت کامل تقسیم در جلوی کسر - به عنوان بخش کامل عدد مختلط - نوشته می شود، و باقیمانده تقسیم در صورت کسر نوشته می شود، مخرج اولیه نیز بدون هیچ تغییری در مخرج پاسخ نوشته می شود.
در اینجا چند مثال از تبدیل کسرهای ناسره به اعداد مختلط را می بینید:
برای تبدیل یک عدد مختلط به یک کسر ناسره، عدد کامل موجود در عدد مختلط را در مخرج کسر ضرب کنید، سپس حاصلضرب را با صورت کسر جمع کنید. نتیجه نهایی را در صورت کسر ناسره قرار دهید، و مخرج کسر بدون تغییر باقی بگذارید.
در اینجا چند مثال از تبدیل اعداد مختلط به کسرهای ناسره را می بینید:


پیدا کردن مخرج های مشترک (common denominators)
مخرج های مشترک (common denominators) - اعداد یکسان در مخرج کسرها - برای عملیات جمع، تفریق، و مقایسه کسرها ضروری می باشند. کسرهای برابر با 1 که با دقت انتخاب شده اند برای ایجاد مخرج های مشترک مورد استفاده قرار می گیرند، زیرا ضرب کسرها در عدد 1 مقدار آنها را تغییر نمی دهد.
برای پیدا کردن یک مخرج مشترک (common denominator) برای دو کسر و نوشتن کسرهای برابر، این مراحل را دنبال کنید:
-
کوچکترین مضرب مشترک (least common multiple) دو کسر را پیدا کنید - کوچکترین عددی که هر دو مخرج بر آن بخش پذیر باشند.
ابتدا، نگاه کنید تا متوجه شوید آیا می توانید صرفاً با یک مشاهده ساده یک مضرب مشترک را به دست آورید، شما ممکن است چند مضرب از هر دو عدد را بدانید. اگر بتوانید صرفاً با مشاهده یک مضرب مشترک بدست آوردید، مستقیماً به مرحله 4 بروید.
-
اگر مضرب مشترک به سادگی مشخص نشود، سپس جستجوی خود را با انتخاب مضرب های بزرگتر آغاز کنید.
-
بررسی کنید تا بدانید آیا مخرج بزرگتر بر مخرج کوچکتر بخش پذیر می باشد.
اگر اینطور نباشد، مضرب های متوالی مخرج بزرگتر را بررسی کنید تا زمانی که مضربی را پیدا کنید که مخرج کوچکتر نیز بر آن بخش پذیر باشد.
-
هنگامی که یک مخرج مشترک پیدا کردید، هر دو کسر را دوباره با مخرج مشترک باز نویسی کنید.
در اینجا چگونگی پیدا کردن یک مخرج مشترک برای دو کسر
-
بررسی کنید تا بدانید آیا می توانید تنها با مشاهده یک مضرب مشترک بین 18 و 24 بیابید.
اعداد 18 و 24 تاحدی بزرگ هستند، بنابراین ممکن است صرفاً با دیدن نتوانید فوراً مضرب مشترکی برای آنها بیابید.
-
تعیین کنید کدام کسر مخرج بزرگتری دارد.
در این مورد، عدد 24 مخرج بزرگتر بین این دو کسر می باشد.
-
بررسی کنید که آیا مخرج بزرگتر بر مخرج کوچکتر بخش پذیر می باشد. اگر اینطور نباشد، مضرب های مخرج بزرگتر را بررسی کنید تا زمانی که موردی را بین آنها بیابید که بر مخرج کوچکتر نیز بخش پذیر باشد.
عدد 24 بر عدد 18 بخش پذیر نمی باشد. دو ضربدر 24 می شود 48، اما 48 نیز بر 18 بخش پذیر نمی باشد. سه ضربدر 24 می شود 72. عدد 72 بر 18 بخش پذیر می باشد. پس مخرج مشترک 72 می باشد.
-
دو کسر را به صورت کسرهای معادلشان با مخرج مشترک یافت شده، باز نویسی کنید. نتیجه تقسیم 72 بر 24 عدد 3 می شود، بنابراین، کسر
را در کسر
ضرب کنید:
نتیجه تقسیم 72 بر 18 عدد 4 می شود، بنابراین کسر
در
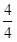 ضرب کنید:
ضرب کنید:
در اینجا چگونگی پیدا کردن کوچکترین مخرج مشترک برای دو کسر
-
بررسی کنید که آیا می توانید صرفاً با مشاهده یک مضرب مشترک بین 25 و 9 مشخص کنید.
به نظر این روش کار نمی کند.
-
مشخص کنید کدام کسر مخرج بزرگتری دارد.
در این مورد 25 مخرج بزرگتر است.
-
بررسی کنید که آیا مخرج بزرگتر بر مخرج کوچکتر بخش پذیر می باشد. اگر اینطور نباشد، مضرب های مخرج بزرگتر را بررسی کنید تا زمانی که مضربی را پیدا کنید که بر مخرج کوچکتر نیز بخش پذیر باشد.
عدد 25 بر 9 بخش پذیر نمی باشد. دو برابر 25 می شود 50، اما 50 نیز بر 9 بخش پذیر نمی باشد. سه برابر 25 می شود 75. عدد 75 نیز بر 9 بخش پذیر نمی باشد. در واقع، شما تا نه برابر 25 که 225 می شود، نمی توانید مضرب مشترکی بیابید.
-
دو کسر را با مخرج مشترک به صورت کسرهای معادلشان باز نویسی کنید.
در اینجا چگونگی این کار را می بنید:
نکته: در این مورد، کوچکترین مخرج مشترک حاصلضرب دو مخرج بود. در صورتی که دو مخرج هیچ فاکتور (factor) مشترکی نداشته باشند این اتفاق می افتد. گاهی اوقات شما می توانید صرفاً با ضرب کردن دو مخرج در یکدیگر به سرعت یک مخرج مشترک بدست آورید. این روش همیشه بهترین و کوچکترین مخرج مشترک را به شما نمی دهد، اما همیشه کارآمد است.
کار کردن با کسرهای ناسره (improper fractions)
همانطور که در ادامه این فصل خواهید دید، ضرب و تقسیم کسرهای ناسره مشکلتر از ضرب و تقسیم کسرهای سره نمی باشد. اگرچه، باز هم همانطور که در ادامه فصل خواهید دید، در صورتی که نتیجه نهایی را به صورت یک عدد مختلط (mixed number) بنویسید، درک آن ساده تر می باشد. همچنین، اگر با یک عدد مختلط آغاز کنید و نیاز داشته باشید که کسرناسره معادل آن را ببینید چه کار باید کنید؟ پاسخ این سوال را در همینجا به شما می دهم.
تبدیل کسرناسره به عددمختلط
برای تبدیل یک کسرناسره به یک عددمختلط، صورت کسر را بر مخرج آن تقسیم کنید. قسمت کامل تقسیم در جلوی کسر - به عنوان بخش کامل عدد مختلط - نوشته می شود، و باقیمانده تقسیم در صورت کسر نوشته می شود، مخرج اولیه نیز بدون هیچ تغییری در مخرج پاسخ نوشته می شود.
در اینجا چند مثال از تبدیل کسرهای ناسره به اعداد مختلط را می بینید:
-
: نتیجه تقسیم عدد 11 بر 9 عدد 1 همراه با 2 باقیمانده می باشد.
-
: نتیجه تقسیم 26 بر 7 عدد 3 همراه با 5 باقیمانده می باشد.
-
: نتیجه تقسیم 402 بر 11 عدد 36 همراه با 6 باقیمانده می باشد. این مثال به صورت مشخص آشکار می سازد که درک اعداد مختلط به مراتب ساده تر از درک کسرهای ناسره می باشد.
تبدیل عدد مختلط به کسرناسره
برای تبدیل یک عدد مختلط به یک کسر ناسره، عدد کامل موجود در عدد مختلط را در مخرج کسر ضرب کنید، سپس حاصلضرب را با صورت کسر جمع کنید. نتیجه نهایی را در صورت کسر ناسره قرار دهید، و مخرج کسر بدون تغییر باقی بگذارید.
در اینجا چند مثال از تبدیل اعداد مختلط به کسرهای ناسره را می بینید:
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: