خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
نقطۀ میانی، مرکز دایره، مرکز مثلث

یک روش برای توصیف وسط یک مثلث اینست که مرکز ثقل (centroid) آن را تعیین کنید. این نقطۀ میانی مرکز جاذبه می باشد، که با استفاده از آن می توانید آن مثلث را متعادل نگه دارید و در اطراف بچرخانید. و وسط یک پاره خط نقطۀ میانی (midpoint) آن می باشد. هنگامی که نمودار یک دایره، مثلث، یا پاره خط را با استفاده از محورهای مختصات ترسیم می کنید، آن گاه می توانید این نقاط میانی را با یک جفت از مختصات های \(x\) و \(y\) نامگذاری کنید. تمام چیزی که برای یافتن این میانه ها نیاز دارید مختصات های برخی از نقاط مهم دیگر بر روی اشکال مربوطه می باشد.

برای یافتن نقطۀ میانی (midpoint) یک پاره خط، شما صرفاً میانگین مختصات ها را محاسبه می کنید ـــ به همین سادگی.
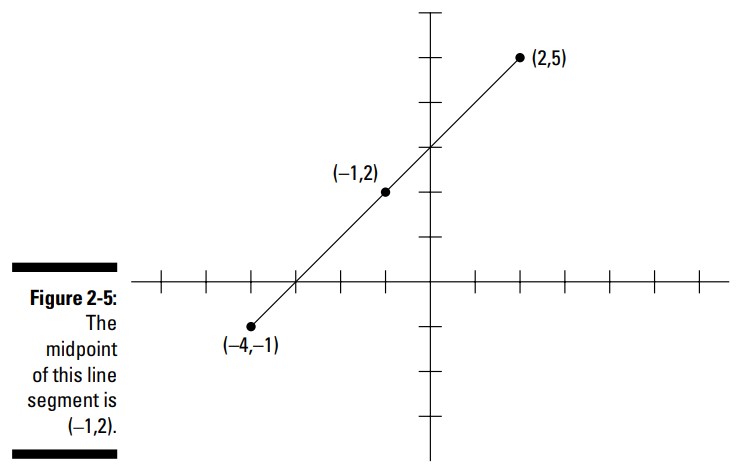
اگر بخواهید نقطۀ میانی پاره خطی با نقاط پایانیِ \((-4,-1)\) و \((2,5)\) را بدانید، این اعداد را در فرمول نقطۀ میانی جایگذاری کنید، تا به نقطۀ میانی \((-1,2)\) برسید:
$$M=\biggl( \frac{-4+2}{2},\frac{-1+5}{2} \biggr)=\biggl( \frac{-2}{2},\frac{4}{2} \biggr)=(-1,2)$$
در شکل 5-2 نمودار این پاره خط را می بینید:
اگر نقاط پایانی یک قطر از یک دایره برابر با \((x_1,y_1)\) و \((x_2,y_2)\) باشند، آن گاه مرکز آن دایره دارای مختصات \(\biggl( \frac{x_1+x_2}{2} ,\frac{y_1+y_2}{2} \biggr)\) می باشد. شما احتمالاً متوجه شدید که مرکز یک دایره، برابر با نقطۀ میانی قطر آن می باشد. مرکز این دایره، قطر آن را به دو پاره خط برابر که شعاع ها نامیده می شوند، تقسیم می کند.
شکل 6-2 دایره ای را با یک قطر نشان می دهد که نقاط پایانی آن برابر با \((7,4)\) و \((-1,-2)\) می باشند. مرکز این دایره در \((3,1)\) می باشد. من مختصات این مرکز را با استفاده از فرمول نقطۀ میانی یک پاره خط بدست آورده ام:
$$M=\biggl( \frac{7+(-1)}{2},\frac{4+(-2)}{2} \biggr) = \bigl( \frac{6}{2},\frac{2}{2} \bigr)=(3,1)$$
شما طول این قطر را با استفاده از فرمول مسافت بدست می آورید:
$$d=\sqrt{(7-(-1))^2 + (4-(-2))^2}=\sqrt{8^2+6^2}=\sqrt{64+36}=\sqrt{100}=10$$
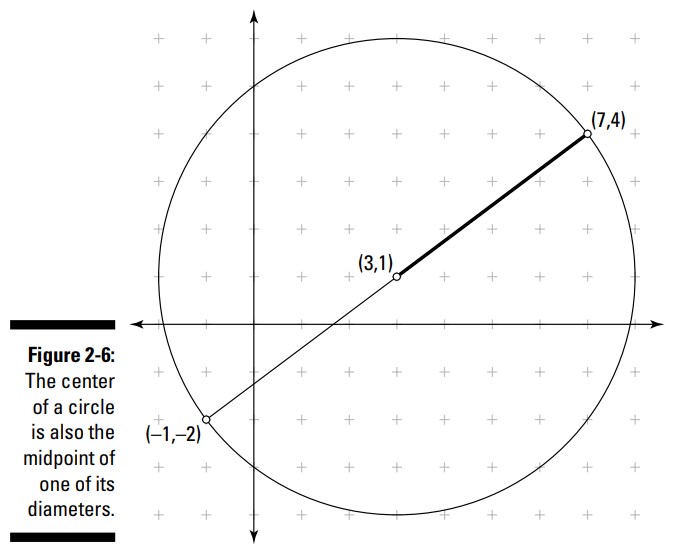
قطر دایره ای که در شکل 6-2 نشان داده شده است، برابر با \(10\) واحد می باشد.
در ادامه، چگونگی یافتن طول یکی از شعاع ها را به شما نشان می دهم. هر کدام که باشد کفایت می کند ـــ طول همۀ آنها یکسان است. در این مثال، من طول شعاع را از مرکز این دایره \((3,1)\) تا نقطۀ پایانی قطر آن \((7,4)\) محاسبه می کنم:
$$d=\sqrt{(7-3)^2 + (4-1)^2} = \sqrt{4^2+3^2}=\sqrt{16+9}=\sqrt{25}=5$$
طول این شعاع \(5\) واحد می باشد. اما، مسلماً، شما انتظار این پاسخ را داشتید، زیرا بنا به تعریف، طول شعاع نصف طول قطر می باشد.
اگر بتوانید نقطۀ میانی یک پاره خط را بیابید، می توانید آن را به دو بخش مساوی تقسیم کنید. یافتن وسط هر کدام از این دو بخش مساوی، به شما امکان می دهد تا نقاطی را بیابید که کل این پاره خط را به چهار بخش مساوی تقسیم کند. یافتن وسط هر کدام از این پاره خطها به شما هشت قسمت مساوی می دهد، و به همین ترتیب.
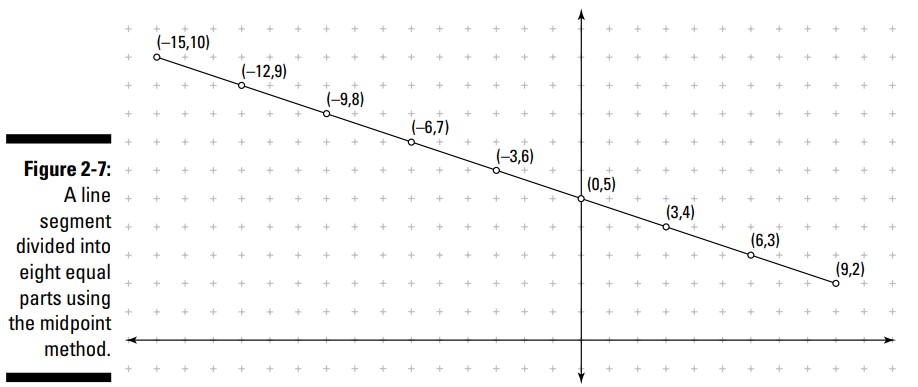
به عنوان مثال، برای اینکه پاره خطی با نقاط پایانیِ \((-15,10)\) و \((9,2)\) را به هشت قسمت مساوی تقسیم کنید، نقاط میانی مختلفی را به این نحو بیابید:
شکل 7-2 مختصات نقاطی که این پاره خط را به هشت قسمت مساوی تقسیم می کنند، نشان می دهد.
مادامیکه صرفاً می خواهید یک پاره خط را به تعداد زوجی از بخشهای مساوی تقسیم کنید، استفاده از روش نقطۀ میانی خوب است. اما کار شما همیشه به این آسانی نیست. به عنوان مثال، ممکن است بخواهید یک پاره خط را به سه بخش مساوی، پنج بخش مساوی، یا تعداد فرد دیگری از بخشهای مساوی تقسیم کنید.
برای یافتن یک نقطه که تا نقاط پایانی یک پاره خط متساوی الفاصله نمی باشد، از فرمول زیر استفاده کنید:
$$(x,y)=\biggl( x_1+k(x_2-x_1), y_1+k(y_2-y_1) \biggr)$$
در این فرمول، \((x_1,y_1)\) نقطۀ پایانی محل آغاز است، \((x_2,y_2)\) نقطۀ پایانی دیگر می باشد، و \(k\) بخش کسری آن پاره خط که می خواهید، می باشد.
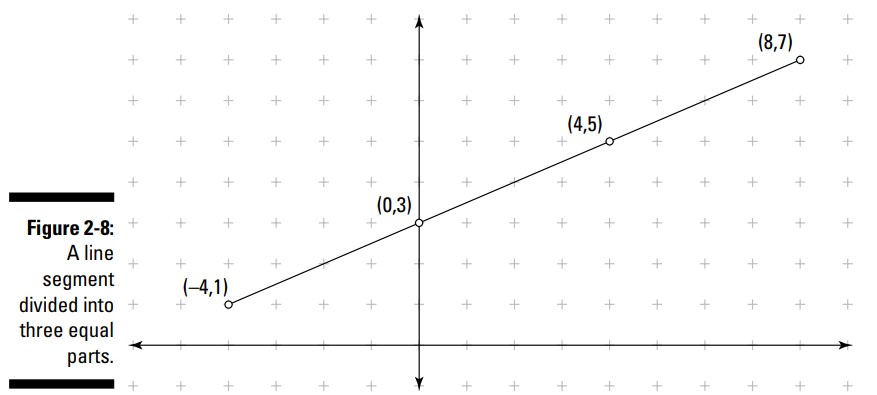
بنابراین، برای یافتن مختصات هایی که پاره خطی با نقاط پایانیِ \((-4,1)\) و \((8,7)\) را به سه بخش مساوی تقسیم می کند، ابتدا نقطه ای را بیابید که یک سوم فاصله از \((-4,1)\) تا نقطۀ پایانی دیگر را دارا باشد، و سپس نقطه ای را بیابید که دو سوم فاصله از \((-4,1)\) تا نقطۀ پایانی دیگر را دارا باشد. مراحل زیر چگونگی این کار را به شما نشان می دهد.
برای یافتن نقطه ای که یک سوم مسافت بین \((-4,1)\) تا نقطۀ پایانی دیگر، \((8,7)\)، می باشد:
برای یافتن نقطه ای که دو سوم فاصلۀ از \((-4,1)\) تا نقطۀ پایانی دیگر، \((8,7)\)، را دارد:
شکل 8-2 نمودار این پاره خط و نقاطی که آن را به سه قسمت برابر تقسیم کرده اند، را نشان می دهد.
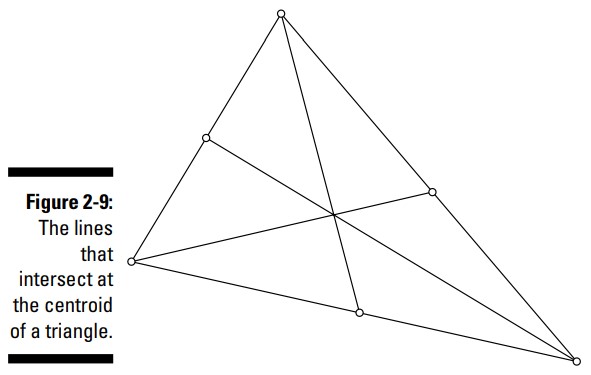
اگر خطهایی را از هر گوشه (یا رأس) یک مثلث به نقاط میانی اضلاع روبروی آنها ترسیم کنید، آن گاه آن سه خط در مرکز، یا مرکز ثقل هندسی (centroid)، آن مثلث، به یکدیگر برخورد می کنند. مرکز ثقل هندسی مثلث مکانی است که آن مثلث به صورت برابر متعادل باقی می ماند. همچنین مختصات های مرکز ثقل دو سوم مسیر بین هر رأس در امتداد آن پاره خط می باشند. شکل 9-2 به شما نشان می دهد چگونه این سه خط در یک مثلث در مرکز به همدیگر برخورد کرده اند.
برای یافتن مرکز ثقل هندسی یک مثلث، از فرمول بخش پیشین استفاده کنید تا مکان نقطه ای را بیابید که دو سوم مسافت بین رأس تا نقطۀ میانی ضلع مقابل را داشته باشد.
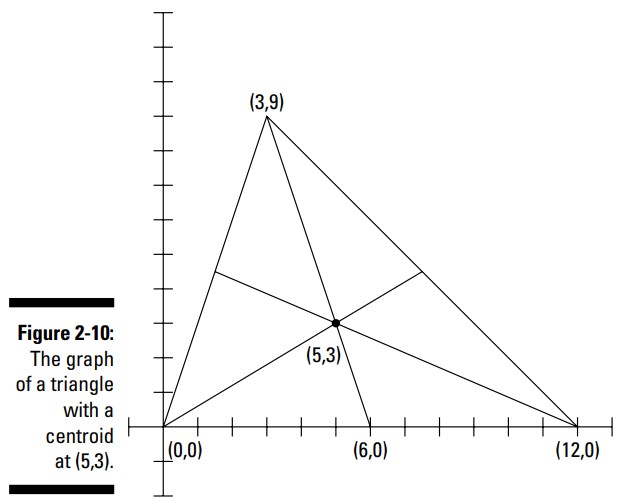
به عنوان مثال، برای یافتن مرکز ثقل هندسی مثلثی با رأس هایی در \((0,0)\)، \((12,0)\)، و \((3,9)\)، ابتدا نقطۀ میانی یکی از اضلاع آن را بیابید. راحتترین ضلع، ضلع پایینی می باشد، زیرا در امتداد محور \(x\) قرار دارد. مختصات های این نقطۀ میانی برابر با \((6,0)\) می باشند. آن گاه نقطه ای را بیابید که در دو سوم مسیر بین رأس مقابل، \((3,9)\)، تا این نقطۀ میانی قرار دارد.
در این مثال، همانطور که در شکل 10-2 می بینید، مرکز ثقل هندسی این مثلث، نقطۀ \((5,3)\) می باشد.

یافتن نقطۀ میانی یک پاره خط
برای یافتن نقطۀ میانی (midpoint) یک پاره خط، شما صرفاً میانگین مختصات ها را محاسبه می کنید ـــ به همین سادگی.
نقطۀ میانی، \(M\) ، در یک پاره خط با نقاط پایانیِ \((x_1,y_1)\) و \((x_2,y_2)\) برابر است با:
$$M=\biggl( \frac{x_1+x_2}{2},\frac{y_1+y_2}{2} \biggr)$$
$$M=\biggl( \frac{x_1+x_2}{2},\frac{y_1+y_2}{2} \biggr)$$
اگر بخواهید نقطۀ میانی پاره خطی با نقاط پایانیِ \((-4,-1)\) و \((2,5)\) را بدانید، این اعداد را در فرمول نقطۀ میانی جایگذاری کنید، تا به نقطۀ میانی \((-1,2)\) برسید:
$$M=\biggl( \frac{-4+2}{2},\frac{-1+5}{2} \biggr)=\biggl( \frac{-2}{2},\frac{4}{2} \biggr)=(-1,2)$$
در شکل 5-2 نمودار این پاره خط را می بینید:

تعیین مرکز یک دایره
اگر نقاط پایانی یک قطر از یک دایره برابر با \((x_1,y_1)\) و \((x_2,y_2)\) باشند، آن گاه مرکز آن دایره دارای مختصات \(\biggl( \frac{x_1+x_2}{2} ,\frac{y_1+y_2}{2} \biggr)\) می باشد. شما احتمالاً متوجه شدید که مرکز یک دایره، برابر با نقطۀ میانی قطر آن می باشد. مرکز این دایره، قطر آن را به دو پاره خط برابر که شعاع ها نامیده می شوند، تقسیم می کند.
شکل 6-2 دایره ای را با یک قطر نشان می دهد که نقاط پایانی آن برابر با \((7,4)\) و \((-1,-2)\) می باشند. مرکز این دایره در \((3,1)\) می باشد. من مختصات این مرکز را با استفاده از فرمول نقطۀ میانی یک پاره خط بدست آورده ام:
$$M=\biggl( \frac{7+(-1)}{2},\frac{4+(-2)}{2} \biggr) = \bigl( \frac{6}{2},\frac{2}{2} \bigr)=(3,1)$$
شما طول این قطر را با استفاده از فرمول مسافت بدست می آورید:
$$d=\sqrt{(7-(-1))^2 + (4-(-2))^2}=\sqrt{8^2+6^2}=\sqrt{64+36}=\sqrt{100}=10$$

قطر دایره ای که در شکل 6-2 نشان داده شده است، برابر با \(10\) واحد می باشد.
در ادامه، چگونگی یافتن طول یکی از شعاع ها را به شما نشان می دهم. هر کدام که باشد کفایت می کند ـــ طول همۀ آنها یکسان است. در این مثال، من طول شعاع را از مرکز این دایره \((3,1)\) تا نقطۀ پایانی قطر آن \((7,4)\) محاسبه می کنم:
$$d=\sqrt{(7-3)^2 + (4-1)^2} = \sqrt{4^2+3^2}=\sqrt{16+9}=\sqrt{25}=5$$
طول این شعاع \(5\) واحد می باشد. اما، مسلماً، شما انتظار این پاسخ را داشتید، زیرا بنا به تعریف، طول شعاع نصف طول قطر می باشد.
تقسیم بندی بیشترِ پاره خطها
اگر بتوانید نقطۀ میانی یک پاره خط را بیابید، می توانید آن را به دو بخش مساوی تقسیم کنید. یافتن وسط هر کدام از این دو بخش مساوی، به شما امکان می دهد تا نقاطی را بیابید که کل این پاره خط را به چهار بخش مساوی تقسیم کند. یافتن وسط هر کدام از این پاره خطها به شما هشت قسمت مساوی می دهد، و به همین ترتیب.
به عنوان مثال، برای اینکه پاره خطی با نقاط پایانیِ \((-15,10)\) و \((9,2)\) را به هشت قسمت مساوی تقسیم کنید، نقاط میانی مختلفی را به این نحو بیابید:
-
نقطۀ میانی پاره خط اصلی از \((-15,10)\) تا \((9,2)\) برابر با \((-3,6)\) می باشد.
-
نقطۀ میانی نصف این پاره خط اصلی، از \((-15,10)\) تا \((-3,6)\) برابر با \((-9,8)\) می باشد، و نقطۀ میانی نصفۀ دیگرِ پاره خط اصلی، از \((-3,6)\) تا \((9,2)\) برابر با \((3,4)\) می باشد.
-
نقاط میانی چهار پاره خطی که تا اینجا مشخص شده اند، عبارت از \((-12,9)\) ، \((-6,7)\) ، \((0,5)\) ، و \((6,3)\) می باشند.
شکل 7-2 مختصات نقاطی که این پاره خط را به هشت قسمت مساوی تقسیم می کنند، نشان می دهد.

مادامیکه صرفاً می خواهید یک پاره خط را به تعداد زوجی از بخشهای مساوی تقسیم کنید، استفاده از روش نقطۀ میانی خوب است. اما کار شما همیشه به این آسانی نیست. به عنوان مثال، ممکن است بخواهید یک پاره خط را به سه بخش مساوی، پنج بخش مساوی، یا تعداد فرد دیگری از بخشهای مساوی تقسیم کنید.
برای یافتن یک نقطه که تا نقاط پایانی یک پاره خط متساوی الفاصله نمی باشد، از فرمول زیر استفاده کنید:
$$(x,y)=\biggl( x_1+k(x_2-x_1), y_1+k(y_2-y_1) \biggr)$$
در این فرمول، \((x_1,y_1)\) نقطۀ پایانی محل آغاز است، \((x_2,y_2)\) نقطۀ پایانی دیگر می باشد، و \(k\) بخش کسری آن پاره خط که می خواهید، می باشد.
بنابراین، برای یافتن مختصات هایی که پاره خطی با نقاط پایانیِ \((-4,1)\) و \((8,7)\) را به سه بخش مساوی تقسیم می کند، ابتدا نقطه ای را بیابید که یک سوم فاصله از \((-4,1)\) تا نقطۀ پایانی دیگر را دارا باشد، و سپس نقطه ای را بیابید که دو سوم فاصله از \((-4,1)\) تا نقطۀ پایانی دیگر را دارا باشد. مراحل زیر چگونگی این کار را به شما نشان می دهد.
برای یافتن نقطه ای که یک سوم مسافت بین \((-4,1)\) تا نقطۀ پایانی دیگر، \((8,7)\)، می باشد:
-
\(-4\) را جایگزین \(x_1\)، \(8\) را جایگزین \(x_2\)، \(1\) را جایگزین \(y_1\) ، \(7\) را جایگزین \(y_2\)، و \(\frac{1}{3}\) را جایگزین \(k\) کنید.
$$(x,y)=\biggl( -4+\frac{1}{3}(8-(-4)), 1+\frac{1}{3}(7-1) \biggr)$$
-
مقادیر پرانتزهای درونی را تفریق کنید.
$$=\biggl( -4+\frac{1}{3}(12),1+\frac{1}{3}(6) \biggr)$$
-
ضرب ها را انجام دهید و سپس نتایج را با یکدیگر جمع کنید تا مختصات ها را بدست آورید.
$$=(-4+4,1+2)=(0,3)$$
برای یافتن نقطه ای که دو سوم فاصلۀ از \((-4,1)\) تا نقطۀ پایانی دیگر، \((8,7)\)، را دارد:
-
\(x_1\) را با \(-4\)، \(x_2\) را با \(8\)، \(y_1\) را با \(1\)، \(y_2\) را با \(7\)، و \(k\) را با \(\frac{2}{3}\) جایگزین کنید.
$$(x,y)=\bigl( -4+\frac{2}{3}(8-(-4)), 1+\frac{2}{3}(7-1) \bigr)$$
-
مقادیر پرانتزهای درونی را تفریق کنید.
$$=\biggl( -4+\frac{2}{3}(12),1+\frac{2}{3}(6) \biggr)$$
-
ضرب ها را انجام دهید و سپس نتایج را با یکدیگر جمع کنید تا مختصات ها را بدست آورید.
$$=(-4+8,1+4)=(4,5)$$
شکل 8-2 نمودار این پاره خط و نقاطی که آن را به سه قسمت برابر تقسیم کرده اند، را نشان می دهد.

تعیین مرکز یک مثلث
اگر خطهایی را از هر گوشه (یا رأس) یک مثلث به نقاط میانی اضلاع روبروی آنها ترسیم کنید، آن گاه آن سه خط در مرکز، یا مرکز ثقل هندسی (centroid)، آن مثلث، به یکدیگر برخورد می کنند. مرکز ثقل هندسی مثلث مکانی است که آن مثلث به صورت برابر متعادل باقی می ماند. همچنین مختصات های مرکز ثقل دو سوم مسیر بین هر رأس در امتداد آن پاره خط می باشند. شکل 9-2 به شما نشان می دهد چگونه این سه خط در یک مثلث در مرکز به همدیگر برخورد کرده اند.

برای یافتن مرکز ثقل هندسی یک مثلث، از فرمول بخش پیشین استفاده کنید تا مکان نقطه ای را بیابید که دو سوم مسافت بین رأس تا نقطۀ میانی ضلع مقابل را داشته باشد.
به عنوان مثال، برای یافتن مرکز ثقل هندسی مثلثی با رأس هایی در \((0,0)\)، \((12,0)\)، و \((3,9)\)، ابتدا نقطۀ میانی یکی از اضلاع آن را بیابید. راحتترین ضلع، ضلع پایینی می باشد، زیرا در امتداد محور \(x\) قرار دارد. مختصات های این نقطۀ میانی برابر با \((6,0)\) می باشند. آن گاه نقطه ای را بیابید که در دو سوم مسیر بین رأس مقابل، \((3,9)\)، تا این نقطۀ میانی قرار دارد.
-
\(x_1\)، \(x_2\)، \(y_1\)، و \(y_2\) را با مقادیر مرتبطشان جایگزین کنید. \(k\) را با \(\frac{2}{3}\) جایگزین کنید.
$$(x,y)=\biggl( 3+\frac{2}{3}(6-(3)),9+\frac{2}{3}(0-9) \biggr)$$
-
محاسبات را ساده سازی کنید تا به این نقطه برسید.
$$=\biggl( 3+\frac{2}{3}(3),9+\frac{2}{3}(-9) \biggr)=(3+2,9-6)=(5,3)$$
در این مثال، همانطور که در شکل 10-2 می بینید، مرکز ثقل هندسی این مثلث، نقطۀ \((5,3)\) می باشد.

لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: