خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
کمان ها و زوایای مرکزی
در این بخش، من کمان ها (arcs) و زوایای مرکزی (central angles) را به شما معرفی می کنم، و سپس شش قضیه در مورد اینکه چگونه کمان ها، زوایای مرکزی، و وترها به یکدیگر مرتبط می باشند، را خواهید دید.

همانطور که در بخشهای بعدی خواهید دید، زوایای مرکزی یک دایره و کمان هایی که این زوایا قطع کرده اند، بخشی از بسیاری از اثبات های دایره ها می باشند. همچنین در بسیاری از مسائل مساحت، که در فصل 15 خواهید دید، ظاهر می گردند. برای یک درک بصری، شکل 2-14 را ببنید.
و در اینجا یک تعریف بیشتر هم داریم که شما برای بخش بعد به آن نیاز پیدا خواهید کرد.
در اینجا یک روش فشرده تر برای فکر کردن به این شش قضیه داریم:
این سه مفهوم را می توان در یک مفهوم فشرده تر هم کرد: اگر هر جفت (از زوایای مرکزی، وترها، یا کمان ها) همنهشت باشند، آن گاه آن دو جفت دیگر نیز با یکدیگر همنهشت خواهند بود.
زمان یک اثبات فرا رسیده است. سعی کنید تا قبل از خواندن پاسخ ارائه شده در کتاب، ابتدا استراتژی بازی خودتان را ایجاد کنید:
داده ها:
دایرۀ \(U\)
\(\overparen{DB} \cong \overparen{WE}\)
\(\overline{UO} \bot \overline{DW}\)
\(\overline{UL} \bot \overline{EB}\)
اثبات کنید:
\(\triangle{UOW} \cong \triangle{ULB}\)
راهنما: جمع و تفریق کمان ها درست همانند جمع و تفریق پاره خطها کار می کند.
اثبات رسمی را ببینید:

این اثبات انجام شد، به سراغ مسألۀ اثبات بعدی می رویم:
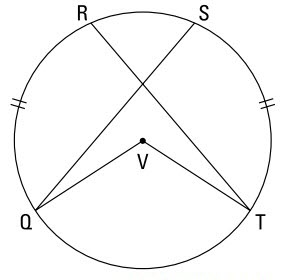
داده ها:
دایرۀ \(V\)
\(\overparen{QR} \cong \overparen{ST}\)
اثبات کنید:
\(\angle{Q} \cong \angle{T}\)
در اینجا یک استراتژی بازی سریع داریم: ابتدا، شعاع هایی را به \(R\) و \(S\) ترسیم کنید، و دو مثلث \(QVS\) و \(TVR\) را بسازید. (در واقع، شش مثلث جدید ایجاد می شوند، اما فقط دو تا از آنها در تمامی رأس هایشان دارای برچسب می باشند؛ آنها مثلث هایی هستند که در این اثبات مورد استفاده قرار می دهید. در مقایسه با مثلث های بدون برچسب، احتمال خیلی بیشتری وجود دارد که این نوع مثلث ها که برچسب دارند، سودمند واقع شوند.) در مورد اینکه چگونه می توانید اثبات کنید مثلث های \(QVS\) و \(TVR\) همنهشت می باشند، فکر کنید. با جمع کمان ها، شما به \(\overparen{QS} \cong \overparen{RT}\) ، و از روی آن، به \(\angle{QVS} \cong \angle{TVR}\) می رسید. سپس با استفاده از آن زوایا و چهار شعاع و با اصل SAS به همنهشتی این دو مثلث می رسید و سپس با CPCTC این مسأله را تمام می کنید.


تعریف کمان (Arc) و زاویه مرکزی (Central angle)
همانطور که در بخشهای بعدی خواهید دید، زوایای مرکزی یک دایره و کمان هایی که این زوایا قطع کرده اند، بخشی از بسیاری از اثبات های دایره ها می باشند. همچنین در بسیاری از مسائل مساحت، که در فصل 15 خواهید دید، ظاهر می گردند. برای یک درک بصری، شکل 2-14 را ببنید.
-
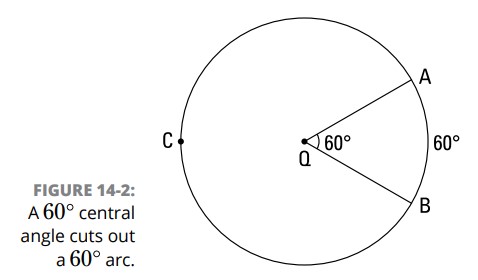
کمان (Arc): یک کمان به سادگی یک قطعۀ منحنی شکل از یک دایره می باشد. هر دو نقطه ای بر روی یک دایره، آن دایره را به دو کمان تقسیم می کنند: یک کمان کوچکتر (minor arc) و یک کمان بزرگتر (major arc) ـــ مگر اینکه آن دو نقطه، نقاط پایانی یک قطر باشند، که در آن مورد هر دوی این کمان ها نیم دایره (semicircle) خواهند بود. شکل 2-14 کمان کوچکتر \(\overparen{AB}\) (یک کمان \(60^{\circ}\)) و کمان بزرگتر \(\overparen{ACB}\) (یک کمان \(300^{\circ}\)) را نشان می دهد. توجه داشته باشید که برای نامگذاری یک کمان کوچکتر، از دو نقطۀ پایانی آن استفاده می کنید؛ برای نامگذاری یک کمان بزرگتر، از دو نقطۀ پایانی آن بعلاوۀ هر نقطۀ دیگری بر روی آن کمان استفاده می کنید.
-
زاویه مرکزی (Central angle): یک زاویۀ مرکزی، زاویه ای است که رأس آن در مرکز یک دایره قرار دارد. دو ضلع یک زاویۀ مرکزی شعاع هایی می باشند که در نقاط پایانی یک کمان، با آن دایره برخورد می کنند ـــ یا به قول ریاضیدانان، این زاویه، آن کمان را جدا می کند (intercepts).
اندازۀ یک کمان همان اندازۀ زاویۀ مرکزی آن که کمان را جدا کرده است، می باشد. این شکل زاویۀ مرکزیِ \(\angle{AQB}\) ، را نشان می دهد که اندازۀ آن ، همانند \(\overparen{AB}\) ، برابر با \(60^{\circ}\) می باشد.
یادداشت مترجم: کمان کوچکتر (minor arc)، با نام کمان اصغر نیز شناخته می شود. همچنین کمان بزرگتر (major arc) با نام قوس اطول نیز شناسایی می گردد.

و در اینجا یک تعریف بیشتر هم داریم که شما برای بخش بعد به آن نیاز پیدا خواهید کرد.
دایره های همنهشت (Congruent circles): دایره های همنهشت، دایره هایی هستند که شعاع های آنها همنهشت باشند.
شش قضیه در مورد دایره ها
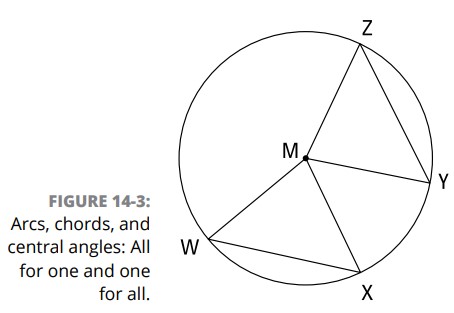
شش قضیۀ زیر همگی صرفاً نسخه های متفاوتی از یک ایدۀ ساده در مورد ارتباطات متقابل بین، کمان ها، زوایای مرکزی، و وترها می باشند (تمامی این شش قضیه در شکل 3-14 نشان داده شده اند):
-
زوایای مرکزی و کمان ها (Central angles and arcs):
-
اگر دو زاویۀ مرکزی در یک دایره (یا در دایره های همنهشت)، همنهشت باشند، آن گاه کمان های بریده شده توسط آنها همنهشت می باشند. (شکل خلاصه: اگر زوایای مرکزی همنهشت باشند، سپس کمان ها همنهشتند.) در شکل 3-14 ، اگر \(\angle{WMX} \cong \angle{ZMY}\) ، آن گاه \(\overparen{WX} \cong \overparen{ZY}\) .
-
اگر دو کمان در یک دایره (یا در دایره های همنهشت)، همنهشت باشند، سپس زوایای مرکزی متناظر آنها همنهشت می باشند. (شکل خلاصه: اگر کمان ها همنهشت باشند، آن گاه زوایای مرکزی همنهشتند.) اگر \(\overparen{WX} \cong \overparen{ZY}\) ، سپس \(\angle{WMX} \cong \angle{ZMY}\) .
-
اگر دو زاویۀ مرکزی در یک دایره (یا در دایره های همنهشت)، همنهشت باشند، آن گاه کمان های بریده شده توسط آنها همنهشت می باشند. (شکل خلاصه: اگر زوایای مرکزی همنهشت باشند، سپس کمان ها همنهشتند.) در شکل 3-14 ، اگر \(\angle{WMX} \cong \angle{ZMY}\) ، آن گاه \(\overparen{WX} \cong \overparen{ZY}\) .
-
زوایای مرکزی و وترها (Central angles and chords):
-
اگر دو زاویۀ مرکزی در یک دایره (یا در دایره های همنهشت)، همنهشت باشند، آن گاه وترهای متناظر آنها همنهشت می باشند. (شکل خلاصه: اگر زوایای مرکزی همنهشت باشند، سپس وترها همنهشتند.) در شکل 3-14، اگر \(\angle{WMX} \cong \angle{ZMY}\) ، سپس \(\overline{WX} \cong \overline{ZY}\)
-
اگر دو وتر در یک دایره (یا در دایره های همنهشت)، همنهشت باشند، آن گاه زوایای مرکزی متناظر آنها همنهشت می باشند. (شکل خلاصه: اگر وترها همنهشت باشند، سپس زوایای مرکزی همنهشتند.) اگر \(\overline{WX} \cong \overline{ZY}\) ، آن گاه \(\angle{WMX} \cong \angle{ZMY}\) .
-
اگر دو زاویۀ مرکزی در یک دایره (یا در دایره های همنهشت)، همنهشت باشند، آن گاه وترهای متناظر آنها همنهشت می باشند. (شکل خلاصه: اگر زوایای مرکزی همنهشت باشند، سپس وترها همنهشتند.) در شکل 3-14، اگر \(\angle{WMX} \cong \angle{ZMY}\) ، سپس \(\overline{WX} \cong \overline{ZY}\)
-
کمان ها و وترها (Arcs and chords):
-
اگر دو کمان در یک دایره (یا در دایره های همنهشت)، همنهشت باشند، آن گاه وترهای متناظر آنها همنهشت می باشند. (شکل خلاصه: اگر کمان ها همنهشت باشند، سپس وترها همنهشتند.) در شکل 3-14 ، اگر \(\overparen{WX} \cong \overparen{ZY}\) ، سپس \(\overline{WX} \cong \overline{ZY}\) .
-
اگر دو وتر در یک دایره (یا در دایره های همنهشت)، همنهشت باشند، آن گاه کمان های متناظر آنها همنهشت می باشند. (شکل خلاصه: اگر وترها همنهشت باشند، سپس کمان ها همنهشتند.) اگر \(\overline{WX} \cong \overline{ZY}\) ، سپس \(\overparen{WX} \cong \overparen{ZY}\) .
-
اگر دو کمان در یک دایره (یا در دایره های همنهشت)، همنهشت باشند، آن گاه وترهای متناظر آنها همنهشت می باشند. (شکل خلاصه: اگر کمان ها همنهشت باشند، سپس وترها همنهشتند.) در شکل 3-14 ، اگر \(\overparen{WX} \cong \overparen{ZY}\) ، سپس \(\overline{WX} \cong \overline{ZY}\) .

در اینجا یک روش فشرده تر برای فکر کردن به این شش قضیه داریم:
-
اگر زوایا همنهشت باشند، هم وترها و هم کمان ها همنهشتند.
-
اگر وترها همنهشت باشند، هم زوایا و هم کمان ها همنهشتند.
-
اگر کمان ها همنهشت باشند، هم وترها و هم زوایا همنهشتند.
این سه مفهوم را می توان در یک مفهوم فشرده تر هم کرد: اگر هر جفت (از زوایای مرکزی، وترها، یا کمان ها) همنهشت باشند، آن گاه آن دو جفت دیگر نیز با یکدیگر همنهشت خواهند بود.
خودتان را با چند اثبات محک بزنید
زمان یک اثبات فرا رسیده است. سعی کنید تا قبل از خواندن پاسخ ارائه شده در کتاب، ابتدا استراتژی بازی خودتان را ایجاد کنید:

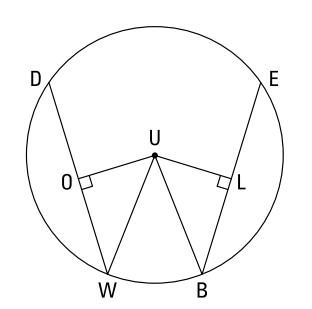
داده ها:
دایرۀ \(U\)
\(\overparen{DB} \cong \overparen{WE}\)
\(\overline{UO} \bot \overline{DW}\)
\(\overline{UL} \bot \overline{EB}\)
اثبات کنید:
\(\triangle{UOW} \cong \triangle{ULB}\)
راهنما: جمع و تفریق کمان ها درست همانند جمع و تفریق پاره خطها کار می کند.
اثبات رسمی را ببینید:

ترجمۀ شکل:
-
دایرۀ \(U\)
\(\overline{UO} \bot \overline{DW}\)
\(\overline{UL} \bot \overline{EB}\)
داده.
-
\(\angle{UOW}\) یک زاویۀ قائمه می باشد
\(\angle{ULB}\) یک زاویۀ قائمه می باشد
تعریف خطهای متعامد.
-
\(\overparen{DB} \cong \overparen{WE}\)
داده.
-
\(\overparen{DW} \cong \overparen{BE}\)
تفریق \(\overparen{WB}\) از \(\overparen{DB}\) و \(\overparen{WE}\) .
-
\(\overline{DW} \cong \overline{BE}\)
اگر کمان ها همنهشت باشند، سپس وترها همنهشت می باشند.
-
\(\overline{UO} \cong \overline{UL}\)
اگر دو وتر از یک دایره همنهشت باشند، سپس آن وترها از مرکز دایره دارای فاصلۀ یکسانی می باشند.
-
\(\overline{UW} \cong \overline{UB}\)
همۀ شعاع ها همنهشت می باشند.
-
\(\triangle{UOW} \cong \triangle{ULB}\)
اصل HLR (گزاره های 2،6،7)
این اثبات انجام شد، به سراغ مسألۀ اثبات بعدی می رویم:

داده ها:
دایرۀ \(V\)
\(\overparen{QR} \cong \overparen{ST}\)
اثبات کنید:
\(\angle{Q} \cong \angle{T}\)
در اینجا یک استراتژی بازی سریع داریم: ابتدا، شعاع هایی را به \(R\) و \(S\) ترسیم کنید، و دو مثلث \(QVS\) و \(TVR\) را بسازید. (در واقع، شش مثلث جدید ایجاد می شوند، اما فقط دو تا از آنها در تمامی رأس هایشان دارای برچسب می باشند؛ آنها مثلث هایی هستند که در این اثبات مورد استفاده قرار می دهید. در مقایسه با مثلث های بدون برچسب، احتمال خیلی بیشتری وجود دارد که این نوع مثلث ها که برچسب دارند، سودمند واقع شوند.) در مورد اینکه چگونه می توانید اثبات کنید مثلث های \(QVS\) و \(TVR\) همنهشت می باشند، فکر کنید. با جمع کمان ها، شما به \(\overparen{QS} \cong \overparen{RT}\) ، و از روی آن، به \(\angle{QVS} \cong \angle{TVR}\) می رسید. سپس با استفاده از آن زوایا و چهار شعاع و با اصل SAS به همنهشتی این دو مثلث می رسید و سپس با CPCTC این مسأله را تمام می کنید.

ترجمۀ شکل:
-
دایرۀ \(V\)
داده.
-
ترسیم \(\overline{VR}\) و \(\overline{VS}\)
دو نقطه یک خط را مشخص می سازند.
-
\(\overline{VR} \cong \overline{VS}\)
تمامی شعاع های در یک دایره همنهشت می باشند.
-
\(\overline{VT} \cong \overline{VQ}\)
تمامی شعاع های در یک دایره همنهشت می باشند.
-
\(\overparen{QR} \cong \overparen{ST}\)
داده.
-
\(\overparen{QS} \cong \overparen{RT}\)
افزودن \(\overparen{RS}\) به هر دو کمان \(\overparen{QR}\) و \(\overparen{ST}\).
-
\(\angle{QVS} \cong \angle{TVR}\)
اگر کمان ها همنشهت باشند، سپس زوایای مرکزی همنشهت می باشند.
-
\(\triangle{QVS} \cong \triangle{TVR}\)
اصل SAS (خطهای 3،7،4). (شما همچنین می توانید در خط 7 به جای استفاده از همنهشتی زوایای متناظر کمان ها از همنهشتی وترهای متناظر کمان ها نیز استفاده کنید و با استفاده از SSS به همنهشتی این دو مثلث برسید.)
-
\(\angle{Q} \cong \angle{T}\)
CPCTC
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: