خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
سه قضیه در مورد تناسب ها

در این بخش شما با سه قضیه آشنا می شوید که شامل تناسب ها در یک جهت یا جهتی دیگر می باشند. اولین قضیه از این قضایا، یک خویشاوند نزدیک با CSSTP می باشد، و دومین قضیه خویشاوند دور آن می باشد. سومین قضیه به هیچ وجه نسبت فامیلی با آن ندارد.

قضیۀ جداکنندۀ ضلع اساساً ضروری نمی باشد زیرا مسأله هایی که در آنها از این قضیه استفاده می کنید، شامل مثلث های متشابه می باشند، بنابراین می توانید با تناسب های معمولی مثلث های متشابه که در همین فصل مطرح کردم، آنها را حل کنید. قضیۀ جداکنندۀ ضلع صرفاً یک روش جایگزین و میانبر را به شما ارائه می دهد.
مسأله زیر، که این قضیه را در عمل به شما نشان می دهد، بررسی کنید:
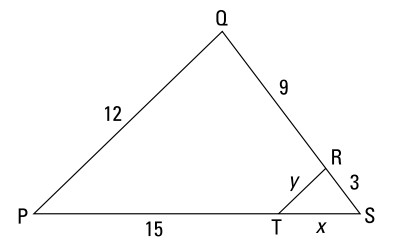
داده ها:
\(\overline{PQ} \parallel \overline{TR}\)
اثبات کنید:
\(\triangle{PQS} \sim \triangle{TRS}\) (اثبات در شکل پاراگراف باشد)
پیدا کنید:
\(x\) و \(y\) را
اثبات اینست: از آنجا که \(\overline{PQ} \parallel \overline{TR}\) ، \(\angle{Q}\) و \(\angle{TRS}\) زوایای همنهشت متناظر می باشند (متناظر از دید قضیۀ خطوط موازی ـــ فصل 10 را ببینید ـــ اما معلوم خواهد شد که این زوایا از منظر دید مثلث های متشابه نیز متناظر می باشند.) سپس، از آنجا که هر دوی این مثلث ها شامل \(\angle{S}\) می باشند، این مثلث ها با \(AA\) متشابه می باشند.
اکنون به سراغ پیدا کردن \(x\) و \(y\) می رویم. از آنجا که \(\overline{PQ} \parallel \overline{TR}\)، شما از قضیۀ جداکنندۀ ضلع برای بدست آوردن \(x\) استفاده می کنید:
$$
\frac{x}{15}=\frac{3}{9}\\
9x=45\\
x=5
$$
و در اینجا راه حل یافتن \(y\) را داریم: ابتدا، مراقب باشید در این تله نیفتید که نتیجه گیری کنید \(y=4\) می باشد. به دو دلیل به نظر می رسد که ضلع \(y\) باید برابر با \(4\) باشد: اول اینکه، به این نتیجه گیری اشتباه برسید که \(\triangle{TRS}\) یک مثلث قائم الزاویۀ \(3-4-5\) است. اما هیچ چیزی در این مسأله به شما نمی گوید که \(\angle{TRS}\) یک زاویۀ قائمه است، بنابراین نمی توانید به این نتیجه گیری برسید.
دوم اینکه، هنگامی که نسبت های \(9:3\) (در امتداد \(\overline{QS}\)) و \(15:5\) (در امتداد \(\overline{PS}\) ، بعد از یافتن \(x\)) می بینید، که هر دوی آنها به \(3:1\) کاهش می یابند، به نظر می رسد که \(PQ\) و \(y\) باید در همان نسبت \(3:1\) باشند. این منجر می شود تا \(PQ:y\) یک نسبت \(12:4\) بسازند، که دوباره شماره به سمت پاسخ اشتباهِ \(y\) برابر است با \(4\) هدایت می کند. این پاسخ به این دلیل اشتباه است که این فرآیند فکری مبتنی بر اینست که قضیۀ جداکنندۀ ضلع برای اضلاعی که جدا نشده اند مورد استفاده قرار گرفته است ـــ که شما مجاز به انجام آن کار نمی باشید.
بنابراین در نهایت، روش صحیح برای بدست آوردن \(y\) استفاده از تناسب معمولی در مثلث های متشابه می باشد. مثلث های موجود در این مسأله به روش یکسانی موقعیت دهی شده اند، بنابراین شما می توانید تناسب های زیر را بنویسید:
$$
\frac{\text{Left side}_{\triangle{TRS}}}{\text{Left side}_{\triangle{PQS}}}=\frac{\text{base}_{\triangle{TRS}}}{\text{base}_{\triangle{PQS}}} \\
\frac{y}{12}=\frac{5}{20} \\
20y=60\\
y=3
$$
تمام شد.
این قضیۀ بعدی، قضیۀ جداکنندۀ ضلع را می گیرد و آن را عمومی می کند، و به آن زمینۀ گسترده تری می دهد. در قضیۀ جداکنندۀ ضلع، شما یک خط موازی ترسیم می کنید که اضلاع یک مثلث را به صورت متناسب تقسیم می کند. با این قضیۀ بعدی، شما می توانید به هر تعداد خطوط موازی ترسیم کنید که هر خطی را (و نه فقط اضلاع یک مثلث را) به صورت متناسب برش می زند.
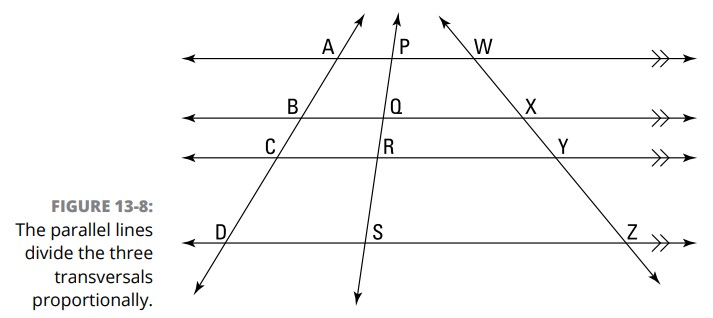
شکل 8-13 را ببینید. با این فرض که خطوط افقی موازی می باشند، نسبتهای زیر از این قضیه حاصل می شوند:
$$
\frac{AB}{BC}=\frac{PQ}{QR}\\
\frac{PQ}{QR}=\frac{WX}{XY}\\
\frac{PR}{RS}=\frac{WY}{YZ}\\
\frac{AD}{BC}=\frac{WZ}{XY}\\
\frac{QS}{PQ}=\frac{XZ}{WX}
$$
برای یک مسأله آماده اید؟ پس بفرمایید:
داده ها:
\(AB=12,BD=32,FJ=33,KM=45,MN=10\)
پیدا کنید:
\(CD,BC,FG,GH,HJ,KL,LM\)
این یک فرآیند طولانی است، بنابراین من مرحله به مرحله به سراغ تک تک طول های مجهول می روم.
در این بخش پایانی، با قضیه دیگری آشنا می شوید که با تناسب ها درگیر است؛ اما برخلاف هر چیز دیگری در این فصل، این قضیه هیچ ارتباطی با تشابه ندارد. (گسترش قضیه جداکنندۀ خط که در بخش پیش مطرح شد، به نظر نمی رسد که با تشابه درگیر باشد، اما به طرز زیرکانه ای مرتبط است.)
هنگامی که یک زاویه از یک مثلث را تنصیف می کنید، هرگز به مثلث های متشابه نمی رسید (مگر اینکه زاویه موجود در رأس یک مثلث متساوی الساقین را تنصیف کنید، که در آن صورت نیمساز آن زاویه آن مثلث را به دو مثلث همنهشت با یکدیگر تقسیم می کند که بدلیل همنهشتی طبیعتاً متشابه نیز می باشند).
با یک مسأله در مورد قضیه نیمساز زاویه، چطورید؟ قطعاً موافقید!
داده ها:
شکل هندسی به نحویکه در این مسأله می بینید
پیدا کنید:
توجه داشته باشید که نسبت بین مساحت این مثلث ها ، یعنی \(9:15\) ، با نسبت بین قاعدۀ این مثلث ها، یعنی \(3:5\) ، برابر است. هرگاه که یک مثلث توسط پاره خطی از یکی از رأس ها به ضلع مقابل به دو مثلث تقسیم گردد (خواه این پاره خط زاویۀ آن رأس را دقیقاً به دو نیم کرده باشد یا خیر)، این برابری حفظ می شود.

قضیۀ جداکنندۀ ضلع (side-splitter theorem)
قضیۀ جداکنندۀ ضلع اساساً ضروری نمی باشد زیرا مسأله هایی که در آنها از این قضیه استفاده می کنید، شامل مثلث های متشابه می باشند، بنابراین می توانید با تناسب های معمولی مثلث های متشابه که در همین فصل مطرح کردم، آنها را حل کنید. قضیۀ جداکنندۀ ضلع صرفاً یک روش جایگزین و میانبر را به شما ارائه می دهد.
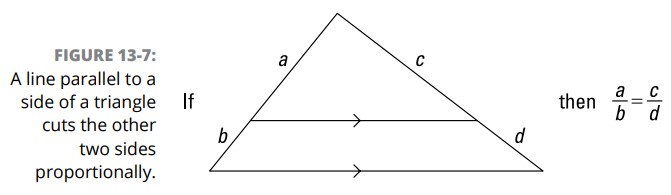
قضیۀ جداکنندۀ ضلع (Side-Splitter Theorem): اگر یک خط با یک ضلع از یک مثلث موازی باشد و دو ضلع دیگر آن مثلث را قطع کند، آن اضلاع را به صورت متناسب تقسیم می کند. شکل 7-13 را ببینید.

مسأله زیر، که این قضیه را در عمل به شما نشان می دهد، بررسی کنید:

داده ها:
\(\overline{PQ} \parallel \overline{TR}\)
اثبات کنید:
\(\triangle{PQS} \sim \triangle{TRS}\) (اثبات در شکل پاراگراف باشد)
پیدا کنید:
\(x\) و \(y\) را
اثبات اینست: از آنجا که \(\overline{PQ} \parallel \overline{TR}\) ، \(\angle{Q}\) و \(\angle{TRS}\) زوایای همنهشت متناظر می باشند (متناظر از دید قضیۀ خطوط موازی ـــ فصل 10 را ببینید ـــ اما معلوم خواهد شد که این زوایا از منظر دید مثلث های متشابه نیز متناظر می باشند.) سپس، از آنجا که هر دوی این مثلث ها شامل \(\angle{S}\) می باشند، این مثلث ها با \(AA\) متشابه می باشند.
اکنون به سراغ پیدا کردن \(x\) و \(y\) می رویم. از آنجا که \(\overline{PQ} \parallel \overline{TR}\)، شما از قضیۀ جداکنندۀ ضلع برای بدست آوردن \(x\) استفاده می کنید:
$$
\frac{x}{15}=\frac{3}{9}\\
9x=45\\
x=5
$$
و در اینجا راه حل یافتن \(y\) را داریم: ابتدا، مراقب باشید در این تله نیفتید که نتیجه گیری کنید \(y=4\) می باشد. به دو دلیل به نظر می رسد که ضلع \(y\) باید برابر با \(4\) باشد: اول اینکه، به این نتیجه گیری اشتباه برسید که \(\triangle{TRS}\) یک مثلث قائم الزاویۀ \(3-4-5\) است. اما هیچ چیزی در این مسأله به شما نمی گوید که \(\angle{TRS}\) یک زاویۀ قائمه است، بنابراین نمی توانید به این نتیجه گیری برسید.
دوم اینکه، هنگامی که نسبت های \(9:3\) (در امتداد \(\overline{QS}\)) و \(15:5\) (در امتداد \(\overline{PS}\) ، بعد از یافتن \(x\)) می بینید، که هر دوی آنها به \(3:1\) کاهش می یابند، به نظر می رسد که \(PQ\) و \(y\) باید در همان نسبت \(3:1\) باشند. این منجر می شود تا \(PQ:y\) یک نسبت \(12:4\) بسازند، که دوباره شماره به سمت پاسخ اشتباهِ \(y\) برابر است با \(4\) هدایت می کند. این پاسخ به این دلیل اشتباه است که این فرآیند فکری مبتنی بر اینست که قضیۀ جداکنندۀ ضلع برای اضلاعی که جدا نشده اند مورد استفاده قرار گرفته است ـــ که شما مجاز به انجام آن کار نمی باشید.
از قضیۀ جداکنندۀ ضلع بر روی اضلاعی که جدا نشده اند، استفاده نکنید. شما از قضیۀ جداکنندۀ ضلع، تنها برای چهار پاره خطی که بر روی اضلاع جدا شدۀ مثلث قرار دارند، می توانید استفاده نمایید. از آن برای اضلاع موازی، که در نسبت متفاوتی می باشند، استفاده نکنید. در مورد اضلاع موازی، از تناسب مثلث های متشابه استفاده نمایید. (هرگاه که یک مثلث توسط خطی که با یکی از اضلاع آن موازی باشد، تقسیم شده باشد، مثلث ایجاد شده با مثلث اصلی، یعنی مثلث بزرگتر، متشابه می باشد.)
بنابراین در نهایت، روش صحیح برای بدست آوردن \(y\) استفاده از تناسب معمولی در مثلث های متشابه می باشد. مثلث های موجود در این مسأله به روش یکسانی موقعیت دهی شده اند، بنابراین شما می توانید تناسب های زیر را بنویسید:
$$
\frac{\text{Left side}_{\triangle{TRS}}}{\text{Left side}_{\triangle{PQS}}}=\frac{\text{base}_{\triangle{TRS}}}{\text{base}_{\triangle{PQS}}} \\
\frac{y}{12}=\frac{5}{20} \\
20y=60\\
y=3
$$
تمام شد.
بسط دادن قضیۀ جداکنندۀ ضلع
این قضیۀ بعدی، قضیۀ جداکنندۀ ضلع را می گیرد و آن را عمومی می کند، و به آن زمینۀ گسترده تری می دهد. در قضیۀ جداکنندۀ ضلع، شما یک خط موازی ترسیم می کنید که اضلاع یک مثلث را به صورت متناسب تقسیم می کند. با این قضیۀ بعدی، شما می توانید به هر تعداد خطوط موازی ترسیم کنید که هر خطی را (و نه فقط اضلاع یک مثلث را) به صورت متناسب برش می زند.
گسترش قضیۀ جداکنندۀ ضلع (Extension of the Side-Splitter Theorem): اگر سه یا بیش از سه خط موازی با دو یا بیش از دو خط متقاطع، برخورد کنند، این خطوط موازی آن خطوط متقاطع را به صورت متناسب تقسیم می کنند.
شکل 8-13 را ببینید. با این فرض که خطوط افقی موازی می باشند، نسبتهای زیر از این قضیه حاصل می شوند:
$$
\frac{AB}{BC}=\frac{PQ}{QR}\\
\frac{PQ}{QR}=\frac{WX}{XY}\\
\frac{PR}{RS}=\frac{WY}{YZ}\\
\frac{AD}{BC}=\frac{WZ}{XY}\\
\frac{QS}{PQ}=\frac{XZ}{WX}
$$

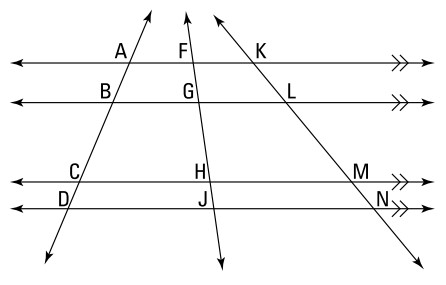
برای یک مسأله آماده اید؟ پس بفرمایید:

داده ها:
\(AB=12,BD=32,FJ=33,KM=45,MN=10\)
پیدا کنید:
\(CD,BC,FG,GH,HJ,KL,LM\)
این یک فرآیند طولانی است، بنابراین من مرحله به مرحله به سراغ تک تک طول های مجهول می روم.
-
یک تناسب برای یافتن \(CD\) ایجاد کنید.
$$
\frac{CD}{AD}=\frac{MN}{KN}\\
\frac{CD}{44}=\frac{10}{55}\\
55 \cdot CD = 44 \cdot 10 \\
CD=8
$$
-
اکنون کافیست \(CD\) را از \(BD\) تفریق کنید تا \(BC\) را بدست آورید.
$$
BD-CD=BC \\
32-8=BC\\
24=BC
$$
-
موقتاً پاره خطهایی که \(\overline{FJ}\) را می سازند، نادیده بگیرید و از یک تناسب برای یافتن \(KL\) استفاده کنید.
$$
\frac{AB}{CD}=\frac{KL}{MN} \\
\frac{12}{8}=\frac{KL}{10} \\
8 \cdot KL = 12 \cdot 10 \\
KL=15
$$
-
با تفریق کردن \(LM\) را بیابید.
$$
KM-KL=LM \\
45-15=LM \\
30=LM
$$
-
برای یافتن بخشهای تشکیل دهندۀ \(\overline{FJ}\) ، از مجموع طول \(\overline{FJ}\) و طول های امتداد \(\overline{AD}\) استفاده کنید.
برای بدست آوردن \(FG\) ، \(GH\) ، و \(HJ\) ، توجه داشته باشید از آنجا که نسبت \(AB:BC:CD\) برابر با \(12:24:8\) می باشد، که به \(3:6:2\) کاهش می یابد، نسبت \(FG:GH:HJ\) نیز باید برابر با \(3:6:2\) باشد. بنابراین اجازه دهید \(FG=3x\) ، \(GH=6x\) ، و \(HJ=2x\) باشد. از آنجا که طول \(\overline{FJ}\) به شما داده شده است، شما می دانید که حاصلجمع این سه پاره خط باید برابر با \(33\) باشد:
$$
3x+6x+2x=33 \\
11x=33 \\
x=3
$$
بنابراین، \(FG=3 \cdot 3 = 9\) ، \(GH=6 \cdot 3 =18\) ، و \(HJ=2 \cdot 3 = 6\) . به همین سادگی.
قضیۀ نیمساز زاویه (angle-bisector theorem)
در این بخش پایانی، با قضیه دیگری آشنا می شوید که با تناسب ها درگیر است؛ اما برخلاف هر چیز دیگری در این فصل، این قضیه هیچ ارتباطی با تشابه ندارد. (گسترش قضیه جداکنندۀ خط که در بخش پیش مطرح شد، به نظر نمی رسد که با تشابه درگیر باشد، اما به طرز زیرکانه ای مرتبط است.)
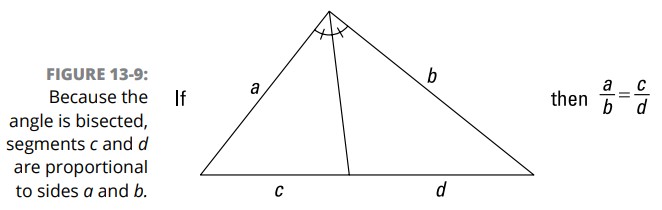
قضیۀ نیمساز زاویه (Angle-Bisector Theorem): اگر یک نیم خط یک زاویه از یک مثلث را تنصیف کند، آن گاه اضلاع روبرو را به پاره خطهایی تقسیم می کند که با دو ضلع دیگر متناسب می باشند. شکل 9-13 را ببینید.

هنگامی که یک زاویه از یک مثلث را تنصیف می کنید، هرگز به مثلث های متشابه نمی رسید (مگر اینکه زاویه موجود در رأس یک مثلث متساوی الساقین را تنصیف کنید، که در آن صورت نیمساز آن زاویه آن مثلث را به دو مثلث همنهشت با یکدیگر تقسیم می کند که بدلیل همنهشتی طبیعتاً متشابه نیز می باشند).
قضیۀ نیمساز زاویه را فراموش نکنید. (به علت برخی از دلایل معمولاً دانش آموزان این قضیه را فراموش می کنند.) بنابراین هرگاه که مثلثی را دیدید که یکی از زوایای آن تنصیف شده باشد، استفاده از این قضیه را در نظر بگیرید.
با یک مسأله در مورد قضیه نیمساز زاویه، چطورید؟ قطعاً موافقید!

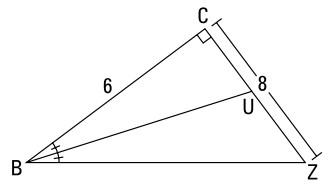
داده ها:
شکل هندسی به نحویکه در این مسأله می بینید
پیدا کنید:
-
\(BZ\) ، \(CU\) ، \(UZ\) ، و \(BU\)
-
مساحت \(\triangle{BCU}\) و \(\triangle{BUZ}\)
-
شما با قضیه فیثاغورث (\(6^2+8^2=c^2\)) یا با توجه به اینکه \(\triangle{BCZ}\) در خانوادۀ مثلث های \(3:4:5\) قرار دارد، \(BZ\) را بدست می آورید. این مثلث یک مثلث \(6-8-10\) می باشد، بنابراین \(BZ\) برابر با \(10\) می باشد.
سپس \(CU\) را برابر با \(x\) و \(UZ\) را برابر با \(8-x\) قرار می دهید. تناسب نیمساز زاویه را ایجاد می کنید و آن را برای یافتن \(x\) حل می کنید:
$$
\frac{6}{10}=\frac{x}{8-x} \\
48-6x=10x \\
48=16x\\
3=x
$$
پس \(CU\) برابر با \(3\) و \(UZ\) برابر با \(5\) می باشد.
سپس \(BU\) را با قضیۀ فیثاغورث بدست می آورید:
$$
(BU)^2=6^2+3^2 \\
(BU)^2=45 \\
BU=\sqrt{45} =3\sqrt{5} \approx 6.7
$$
-
مساحت \(\triangle{BCU}\) و \(\triangle{BUZ}\) را محاسبه کنید.
هر دوی این مثلثها دارای ارتفاع \(6\) می باشند (هنگامی که از \(\overline{CU}\) و \(\overline{UZ}\) به عنوان قاعده های آنها استفاده می کنید)، بنابراین کافیست از فرمول مساحت مثلث استفاده کنید:
$$
Area_{\triangle{}}={1\over2}bh \\
Area_{\triangle{BCU}}={1\over2} \cdot 3 \cdot 6 = 9 \text{ units}^2 \\
Area_{\triangle{BUZ}}={1\over2} \cdot 5 \cdot 6 = 15 \text{ units}^2
$$
توجه داشته باشید که نسبت بین مساحت این مثلث ها ، یعنی \(9:15\) ، با نسبت بین قاعدۀ این مثلث ها، یعنی \(3:5\) ، برابر است. هرگاه که یک مثلث توسط پاره خطی از یکی از رأس ها به ضلع مقابل به دو مثلث تقسیم گردد (خواه این پاره خط زاویۀ آن رأس را دقیقاً به دو نیم کرده باشد یا خیر)، این برابری حفظ می شود.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: