خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
مثلث های قائم الزاویۀ خاص

مثلث های قائم الزاویه آب نبات های کوچک خوشمزه ای هستند. ارتباط بین طول اضلاع آنها به شما کمک می کند تا ضلعی را که نمی توانید به آن برسید، اندازه گیری کنید. و درست زمانیکه شما فکر می کنید ریاضی دیگر از این بهتر نمی شود، دو مثلث عالی از راه می رسند (شکل 6-6 را ببینید). یکی از آنها یک مثلث متساوی الساقین قائم الزاویه می باشد. دو ساق آن یکسان هستند، و وتر آن همواره مضربی از طول آنها می باشد. مثلث قائم الزاویۀ خاص دیگر دارای یک ضلع است که نصف اندازۀ ضلع دیگر می باشد. این دو مثلث بسیار مفید هستند، زیرا اندازۀ زوایا در آنها از رایج ترین ها می باشند، و اندازۀ اضلاع آنها در توابع مثلثاتی مورد استفاده قرار می گیرند.

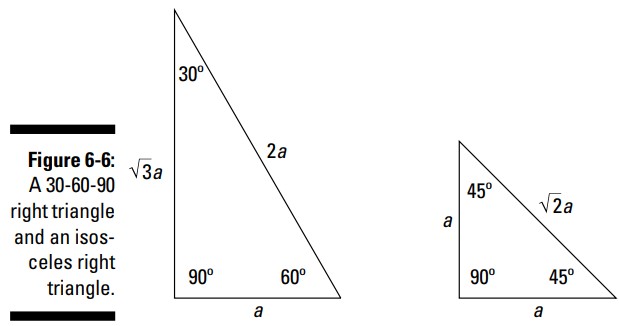
یک مثلث قائم الزاویۀ \(\text{30-60-90}\) دارای اندازۀ زوایایی می باشد که نام آن بیان می دارد. دو زاویۀ حادۀ، مکمل آن برابر با \(30\) و \(60\) درجه می باشند. این مثلث ها برای کار کردن عالی هستند، زیرا اندازۀ زوایا، همگی مضربی از \(30\) می باشند، دارای الگو هستند، و اندازۀ اضلاع آن نیز همینطور هستند. اوه، بله، قضیۀ فیثاغورث هنوز هم برقرار است ـــ شما آن ارتباط بین مربع این اضلاع را دارید. اما، علاوه بر آن \(a\)، \(b\)، و \(c\) به روش دیگری نیز به یکدیگر مرتبط هستند. در یک مثلث قائم الزاویۀ \(\text{30-60-90}\)، اگر \(a\) کوتاهترین ضلع باشد، سپس وتر آن، طولانی ترین ضلع، دوبرابر آن یا \(2a\) می باشد. شما می توانید به جای حرف \(c\) از \(2a\) استفاده کنید. و ضلع متوسط برابر با \(\sqrt{3}a\) یا در حدود \(1.7\) برابر کوتاهترین ضلع می باشد؛ این عدد جایگزین حرف \(b\) می شود. بخش بسیار زیبای مربوط به این مثلث اینست که شما می توانید هر سه ضلع آن را به لحاظ یک متغیر، \(a\)، بنویسید. ببینید این اضلاع چگونه در قضیۀ فیثاغورث جای می گیرند:
$$
a^2+\bigl( \sqrt{3}a \bigr)^2 = \bigl(2a \bigr)^2 \\
a^2 + 3a^2=4a^2
$$
در اینجا یک مسالۀ نمونه داریم که می توانید با بهره بردن از ارتباطات خاص درون یک مثلث قائم الزاویۀ \(\text{30-60-90}\) آن را حل کنید: اگر وتر یک مثلث قائم الزاویۀ خاص دارای \(8\) واحد طول باشد، سپس اندازۀ دو ضلع دیگر آن چقدر می باشند؟
مثلث قائم الزاویۀ خاص دیگر، مثلث قائم الزاویۀ متساوی الساقین (isosceles right triangle) یا مثلث \(\text{45-45-90}\) می باشد. دو زاویۀ حاده در این مثلث برابرند، که منجر می شود تا دو ضلع روبروی این زوایا نیز با یکدیگر برابر گردند. آیا چیز بیشتری هم هست؟ بله! طول آن دو ضلع دارای یک رابطۀ خاص با وتر می باشند (مسلماً علاوه بر رابطۀ قضیۀ فیثاغورث). در یک مثلث قائم الزاویۀ متساوی الساقین، اگر هر کدام از ساق ها دارای \(a\) واحد طول باشند، آن گاه وتر برابر با \(\sqrt{2}a\) یا در حدود \(1.4\) برابر یک ساق، می باشد.
اکنون که می دانید مثلث های قائم الزاویۀ متساوی الساقین، چگونه کار می کنند، این مسالۀ نمونه را امتحان کنید: اگر یک مثلث قائم الزاویۀ متساوی الساقین دارای وتری به طول \(16\) واحد باشد، آن گاه اندازۀ ساق های آن چقدر هستند؟


مثلث قائم الزاویۀ \(\text{30-60-90}\)
یک مثلث قائم الزاویۀ \(\text{30-60-90}\) دارای اندازۀ زوایایی می باشد که نام آن بیان می دارد. دو زاویۀ حادۀ، مکمل آن برابر با \(30\) و \(60\) درجه می باشند. این مثلث ها برای کار کردن عالی هستند، زیرا اندازۀ زوایا، همگی مضربی از \(30\) می باشند، دارای الگو هستند، و اندازۀ اضلاع آن نیز همینطور هستند. اوه، بله، قضیۀ فیثاغورث هنوز هم برقرار است ـــ شما آن ارتباط بین مربع این اضلاع را دارید. اما، علاوه بر آن \(a\)، \(b\)، و \(c\) به روش دیگری نیز به یکدیگر مرتبط هستند. در یک مثلث قائم الزاویۀ \(\text{30-60-90}\)، اگر \(a\) کوتاهترین ضلع باشد، سپس وتر آن، طولانی ترین ضلع، دوبرابر آن یا \(2a\) می باشد. شما می توانید به جای حرف \(c\) از \(2a\) استفاده کنید. و ضلع متوسط برابر با \(\sqrt{3}a\) یا در حدود \(1.7\) برابر کوتاهترین ضلع می باشد؛ این عدد جایگزین حرف \(b\) می شود. بخش بسیار زیبای مربوط به این مثلث اینست که شما می توانید هر سه ضلع آن را به لحاظ یک متغیر، \(a\)، بنویسید. ببینید این اضلاع چگونه در قضیۀ فیثاغورث جای می گیرند:
$$
a^2+\bigl( \sqrt{3}a \bigr)^2 = \bigl(2a \bigr)^2 \\
a^2 + 3a^2=4a^2
$$
در اینجا یک مسالۀ نمونه داریم که می توانید با بهره بردن از ارتباطات خاص درون یک مثلث قائم الزاویۀ \(\text{30-60-90}\) آن را حل کنید: اگر وتر یک مثلث قائم الزاویۀ خاص دارای \(8\) واحد طول باشد، سپس اندازۀ دو ضلع دیگر آن چقدر می باشند؟
-
طول ساق کوتاهتر را بیابید.
وتر دوبرابر ضلع کوتاهتر، \(a\)، می باشد. بنابراین \(8=2a\). آن را بر \(2\) تقسیم کنید و به نتیجۀ \(a=4\) می رسید.
-
طول ساق بلندتر را بیابید.
ساق بلندتر برابر با \(\sqrt{3}a\) می باشد، بنابراین با ضرب کردن \(\sqrt{3}\) در \(4\) به \(4\sqrt{3}\)، یا در حدود \(6.9\) واحد، می رسید.
مثلث های قائم الزاویۀ متساوی الساقین
مثلث قائم الزاویۀ خاص دیگر، مثلث قائم الزاویۀ متساوی الساقین (isosceles right triangle) یا مثلث \(\text{45-45-90}\) می باشد. دو زاویۀ حاده در این مثلث برابرند، که منجر می شود تا دو ضلع روبروی این زوایا نیز با یکدیگر برابر گردند. آیا چیز بیشتری هم هست؟ بله! طول آن دو ضلع دارای یک رابطۀ خاص با وتر می باشند (مسلماً علاوه بر رابطۀ قضیۀ فیثاغورث). در یک مثلث قائم الزاویۀ متساوی الساقین، اگر هر کدام از ساق ها دارای \(a\) واحد طول باشند، آن گاه وتر برابر با \(\sqrt{2}a\) یا در حدود \(1.4\) برابر یک ساق، می باشد.
اکنون که می دانید مثلث های قائم الزاویۀ متساوی الساقین، چگونه کار می کنند، این مسالۀ نمونه را امتحان کنید: اگر یک مثلث قائم الزاویۀ متساوی الساقین دارای وتری به طول \(16\) واحد باشد، آن گاه اندازۀ ساق های آن چقدر هستند؟
-
معادله ای برای حل کردن ایجاد کنید.
وتر برابر با \(\sqrt{2}a\) می باشد، که در آن \(a\) طول ساق ها می باشد. شما می دانید که وتر برابر با \(16\) است، پس می توانید معادلۀ \(\sqrt{2}a=16\) را برای طول \(a\) حل کنید.
-
معادله را برای بدست آوردن \(a\) حل کنید.
هر دو سمت معادله را بر رادیکال تقسیم کنید تا به نتیجۀ زیر برسید:
$$
\frac{\sqrt{2}a}{\sqrt{2}}=\frac{16}{\sqrt{2}} \\
a = \frac{16}{\sqrt{2}} =\frac{16}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{16\sqrt{2}}{2} = 8\sqrt{2}
$$
هر ساق در حدود \(11.3\) واحد می باشد.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: