خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
معکوس توابع مثلثاتی: کسکانت، سکانت، و کتانژانت

سه تابع مثلثاتی پایه ای (سینوس، کسینوس، و تانژانت) از سه ضلع یک مثلث استفاده می کنند، در آنِ واحد دو تا از این اضلاع را می گیرند و نسبت ها/کسرهایی را از آنها می سازند. اما سه تابع مثلثاتی دیگر نیز وجود دارند، و توابع معکوس نامیده می شوند، زیرا از معکوس ها یا وارون های سه تابع مثلثاتی اصلی استفاده می کنند. اگر این سه تابع دیگر صرفاً معکوس سه تابع اول هستند، اصلاً چرا ضرورت دارند؟ شما احتمالاً بدون آنها هم می توانید به زندگی تان ادامه بدهید، اما سرانجام هنگام انجام محاسبات و حل کردن معادلات، کمبود آنها را احساس خواهید کرد. هنگام حل کردن یک معادله، داشتن یک متغیر مجهول در صورت یک کسر، زیباتر و راحتتر از اینست که متغیری را در مخرج آن کسر داشته باشید، و این توابع معکوس این وضعیتها را ممکن می سازند. مسأله چیزی فراتر از راحتی نیست، اما من برای این لوکس بازی ها کاملاً پایه هستم.

تابع کسکانت (cosecant)، که مخفف آن csc می باشد، معکوس تابع سینوس است و از اینرو از این نسبت استفاده می کند: \(\frac{\text{hypotenuse}}{\text{opposite}}\) (وتر بر روی ضلع روبرو). وتر در یک مثلث قائم الزاویه همواره بلندترین ضلع است، بنابراین صورت این کسر همواره بزرگتر از مخرج آن می باشد. در نتیجه، تابع کسکانت همواره مقادیری بزرگتر از \(1\) را تولید می کند.
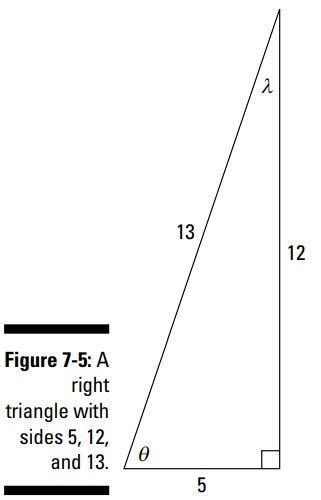
شما می توانید از مقادیر موجود در شکل 5-7 برای تعیین کسکانت این دو زاویۀ حاده استفاده کنید: \(\csc \theta = \frac{13}{12}\) و \(\csc \lambda = \frac{13}{5}\) .
فرض کنید کسی از شما می خواهد تا کسکانت زاویۀ \(\alpha\) را بیابید، و برای شما معلوم باشد که وتر برابر با \(1\) واحد و آن مثلث قائم الزاویه متساوی الساقین باشد. یادتان باشد که مثلث متساوی الساقین دارای دو ضلع برابر می باشد. این دو ضلع باید دو ساق این مثلث باشند، زیرا وتر باید طولانی ترین ضلع باشد. بنابراین، برای یافتن کسکانت:
تابع سکانت (secant)، که مخفف آن sec می باشد، معکوس تابع کسینوس است. بنابراین نسبت آن برابر با \(\frac{\text{hypotenuse}}{\text{adjacent}}\) است. درست مانند کسکانت، نسبت این اضلاع بزرگتر از \(1\) می باشد. با استفاده از مثلث موجود در شکل 5-7، سکانت دو زاویه حاده عبارت از \(\sec \theta = \frac{13}{5}\) و \(\sec \lambda=\frac{13}{12}\) می باشند.
آخرین تابع معکوس، کتانژانت (cotangent) می باشد، که مخفف آن cot است. این تابع معکوس تانژانت می باشد. نسبت اضلاع در کتانژانت برابر با \(\frac{\text{adjacent}}{\text{opposite}}\) می باشد. بنابراین، اگر به شکل 5-7 بازگردید، خواهید دید که کتانژانت دو زاویۀ حاده برابر با \(\cot \theta = \frac{5}{12}\) و \(\cot \lambda = \frac{12}{5}\) می باشند.
گاهی اوقات شما مقدار کتانژانت را همراه با سایر اطلاعات می دانید و مجبور هستید تا آن را برای بدست آوردن یکی از اضلاع یا هر دو ضلع مورد استفاده قرار دهید. این مثال را امتحان کنید: طول ساقهای یک مثلث قائم الزاویه که \(\cot = \frac{11}{60}\) و وتر آن برابر با \(183\) اینچ می باشد، چقدر است؟

تابع کسکانت: معکوس تابع سینوس
تابع کسکانت (cosecant)، که مخفف آن csc می باشد، معکوس تابع سینوس است و از اینرو از این نسبت استفاده می کند: \(\frac{\text{hypotenuse}}{\text{opposite}}\) (وتر بر روی ضلع روبرو). وتر در یک مثلث قائم الزاویه همواره بلندترین ضلع است، بنابراین صورت این کسر همواره بزرگتر از مخرج آن می باشد. در نتیجه، تابع کسکانت همواره مقادیری بزرگتر از \(1\) را تولید می کند.
شما می توانید از مقادیر موجود در شکل 5-7 برای تعیین کسکانت این دو زاویۀ حاده استفاده کنید: \(\csc \theta = \frac{13}{12}\) و \(\csc \lambda = \frac{13}{5}\) .

فرض کنید کسی از شما می خواهد تا کسکانت زاویۀ \(\alpha\) را بیابید، و برای شما معلوم باشد که وتر برابر با \(1\) واحد و آن مثلث قائم الزاویه متساوی الساقین باشد. یادتان باشد که مثلث متساوی الساقین دارای دو ضلع برابر می باشد. این دو ضلع باید دو ساق این مثلث باشند، زیرا وتر باید طولانی ترین ضلع باشد. بنابراین، برای یافتن کسکانت:
-
طول این دو ساق را بیابید.
قضیۀ فیثاغورث بیان می دارد که \(a^2+b^2=c^2\)، اما از آنجا که این دو ضلع همنهشت هستند، شما می توانید یک متغیر بگیرید و این معادله را به شکل \(a^2+a^2=c^2\) . \(1\) را به جای \(c\) قرار دهید و آن را برای بدست آوردن \(a\) حل کنید.
$$
2a^2=1 \\
a^2=\frac{1}{2} \\
a=\sqrt{\frac{1}{2}} \\
a=\frac{1}{\sqrt{2}}
$$
طول هر دو ساق برابر با \(\frac{1}{\sqrt{2}}\) واحد می باشند. شما می توانید رادیکال را در مخرج کسر رها کنید و در مورد گویا کردن (از زیر رادیکال در آوردن) نگران نباشید، زیرا شما قصد دارید تا کل این چیزها را در نسبت کسکانت قرار دهید، به هر حال، چیزها تغییر خواهند کرد.
-
از طول ضلع روبرو در نسبت کسکانت استفاده کنید.
$$\csc \alpha = \frac{\text{hypotenuse}}{\text{opposite}} = \frac{1}{\frac{1}{\sqrt{2}}}=\sqrt{2}$$
تابع سکانت: معکوس تابع کسینوس
تابع سکانت (secant)، که مخفف آن sec می باشد، معکوس تابع کسینوس است. بنابراین نسبت آن برابر با \(\frac{\text{hypotenuse}}{\text{adjacent}}\) است. درست مانند کسکانت، نسبت این اضلاع بزرگتر از \(1\) می باشد. با استفاده از مثلث موجود در شکل 5-7، سکانت دو زاویه حاده عبارت از \(\sec \theta = \frac{13}{5}\) و \(\sec \lambda=\frac{13}{12}\) می باشند.
تابع کتانژانت: معکوس تابع تانژانت
آخرین تابع معکوس، کتانژانت (cotangent) می باشد، که مخفف آن cot است. این تابع معکوس تانژانت می باشد. نسبت اضلاع در کتانژانت برابر با \(\frac{\text{adjacent}}{\text{opposite}}\) می باشد. بنابراین، اگر به شکل 5-7 بازگردید، خواهید دید که کتانژانت دو زاویۀ حاده برابر با \(\cot \theta = \frac{5}{12}\) و \(\cot \lambda = \frac{12}{5}\) می باشند.
نسبت کتانژانت صرفاً نسبت آن می باشد، و نه الزاماً طول اضلاع آن. کسری که توسط این اضلاع ساخته می شود، ممکن است با تقسیم صورت و مخرج آن در عددی یکسان، کاهش یابد.
گاهی اوقات شما مقدار کتانژانت را همراه با سایر اطلاعات می دانید و مجبور هستید تا آن را برای بدست آوردن یکی از اضلاع یا هر دو ضلع مورد استفاده قرار دهید. این مثال را امتحان کنید: طول ساقهای یک مثلث قائم الزاویه که \(\cot = \frac{11}{60}\) و وتر آن برابر با \(183\) اینچ می باشد، چقدر است؟
-
اضلاع مجاور و روبرو را به شکل مضرب هایی از عددی یکسان بنویسید، \(m\)، و آنها را همراه با وتر در قضیۀ فیثاغورث قرار دهید.
$$(11m)^2+(60m)^2=183^2$$
-
این معادله را ساده کنید و آن را برای بدست آوردن \(m\) حل کنید.
$$
(11m)^2+ (60m)^2=183^2 \\
121m^2+3,600m^2=33,489 \\
3,721m^2=33,489 \\
m^2=\frac{33,489}{3,721}=9 \\
m=3
$$
-
از مقدار \(m\) برای پیدا کردن طول این دو ساق استفاده کنید.
از آنجا که می دانید \(m=3\)، خواهید دانست که ضلع مجاور برابر با \(11m=11(3)=33\) است، و ضلع روبرو برابر با \(60m=60(3)=180\) است. سه ضلع این مثلث قائم الزاویه برابر با \(33\)، \(180\)، و \(183\) می باشند. شما می توانید با جایگذاری این سه عدد در قضیۀ فیثاغورث و اطمینان حاصل کردن از اینکه این قضیه برقرار می باشد، پاسخهایتان را درست آزمایی کنید.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (2 دیدگاه)
دیدگاه خود را ثبت کنید: