خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
کاربرد نمودارهای توابع مثلثاتی

نگاه کردن به نمودارهای توابع مثلثاتی که می توانید با ویرایش توابع یا ترکیب آنها بدست آورید، می تواند سرگرم کننده باشد. حتی می توانند در هنگام فراهم آوردن یک حاشیۀ خاص یا سایر آثار هنری، سودمند باشند. اما کاربردهای عملی این نمودارها چیزی است که در این بخش مطرح می شوند. یک متخصص قلب و عروق، به نمودار کارکرد قلب نگاه می کند و تشخیص می دهد که آیا آن قلب بدرستی می تپد یا خیر. نمودارهای فعالیت زلزله ها از چیزهای مورد علاقۀ افرادی است که امیدوارند تا زلزلۀ بعدی را پیش بینی کنند ـــ البته با زمان کافی که بتوانند همه را آگاه سازند.

در امتداد ساحل، جزر و مدها از علاقه مندیهای خاص می باشند. جزر و مدها توسط کشش گرانشی خورشید و ماه تحت تاثیر قرار می گیرند. جزر و مدهای دارای ارتفاع بالا و جزر و مدهای دارای ارتفاع پایین، یک الگوی تناوبی را دنبال می کنند که می توانید با تابع سینوس آنها را مدل سازی کنید. در نیمه شب یک روز زمستانی خاص، جزر و مد بلندی در بوستون ماساچوست اتفاق افتاد. برای تعیین ارتفاع آب در بندر، از معادلۀ \(H(t)=4.8 \sin [\frac{\pi}{6}(t+3)]+5.1\) ، استفاده کنید، که در آن \(t\) نشان دهندۀ تعداد ساعات بعد از نیمه شب است.
نمودار این بخش جمعیت یک گله گوزن را از اول آوریل تا آوریل سال بعد، نشان می دهد. گوزن های جدید در بهار متولد می شوند، بنابراین افزایش در اندازۀ گله انتظار می رود. شکارچیان (درندگان) به دنبال گوزن های ضعیفند ـــ هم جوان و هم پیر. و سپس شما باید آب و هوا را در نظر بگیرید؛ زمستان می تواند برای این جمعیت بسیار سخت باشد. به نمودار موجود در شکل 8-22 بنگرید و بررسی کنید که آیا آن چیزی را که انتظارش را داشتید، نشان می دهد یا خیر. این چرخه نتیجۀ یافتن مجموع دو تابع سینوس مختلف می باشد:
$$D(m)=400+40 \sin (0.524m)+20 \sin (1.047m)$$
این تابع نشان دهندۀ جمعیت گله می باشد، در این تابع \(m\) تعداد ماهها از آوریل می باشد.
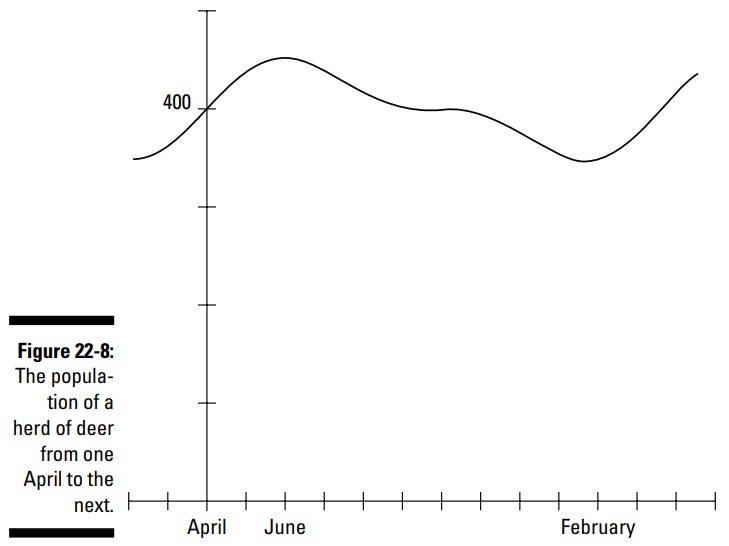
این گله بالاترین تعداد یعنی \(450\) گوزن را در ژوئن و کمترین تعداد یعنی \(350\) گوزن را در فوریه، تجربه می کند. این مدل گله ای را نشان می دهد که تقریباً از سالی به سال دیگر اندازه اش یکسان باقی می ماند.
در این بخش، یک تابع مثلثاتی مدلی را برای یک شیء متصل به یک فنر اثبات می کند. مشابه بخشهای قبلی، الگوی یکسانی بارها و بارها تکرار نمی شود. اما این یک مثال عالی از یک تابع مثلثاتی در عمل می باشد.
معادلۀ \(H(t)=3(0.7)^t \cos 5t+4\) نشان دهندۀ ارتفاع یک شیء متصل به یک فنر می باشد، که در آن \(t\) نشان دهندۀ مقدار زمانی است که گذشته است ـــ معمولاً در واحد ثانیه. این معادله یک تابع مثلثاتی دارد که در یک تابع نمایی ضرب شده است. هنگامی که در ابتدا این فنر را رها می کنید، این شیء به ارتفاعی حدود \(7\) فوت می رسد. آن شیء بالا و پایین می جهد، سرانجام در حدود ارتفاع \(4\) فوتی آرام می گیرد، شکل 9-22 این امر را نشان می دهد.
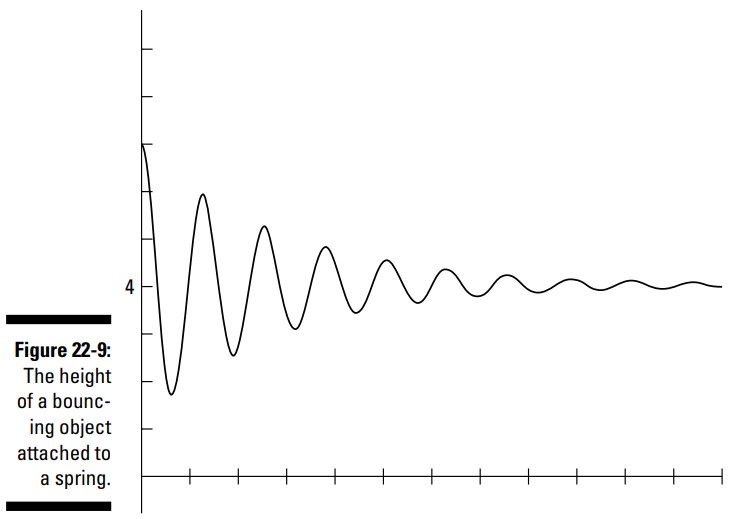
شما احتمالاً با مدلی مشابه این مدل در هنگام نشان دادن بالا و پایین رفتن فردی که بانجی جامپینگ می کند، مواجه شوید. بنابراین، می توانید ببینید که توابع مثلثاتی انواع مختلف کاربردها را دارند ـــ بسیاری از این کاربردها خیلی سودمند هستند.

اندازه گیری جزر و مد
در امتداد ساحل، جزر و مدها از علاقه مندیهای خاص می باشند. جزر و مدها توسط کشش گرانشی خورشید و ماه تحت تاثیر قرار می گیرند. جزر و مدهای دارای ارتفاع بالا و جزر و مدهای دارای ارتفاع پایین، یک الگوی تناوبی را دنبال می کنند که می توانید با تابع سینوس آنها را مدل سازی کنید. در نیمه شب یک روز زمستانی خاص، جزر و مد بلندی در بوستون ماساچوست اتفاق افتاد. برای تعیین ارتفاع آب در بندر، از معادلۀ \(H(t)=4.8 \sin [\frac{\pi}{6}(t+3)]+5.1\) ، استفاده کنید، که در آن \(t\) نشان دهندۀ تعداد ساعات بعد از نیمه شب است.
-
مقدار \(t\) را در این معادله قرار دهید.
در نیمه شب، مقدار \(t\) برابر با \(0\) می باشد. جایگذاری \(0\) در \(t\) در این معادله نتیجۀ زیر را به شما می دهد:
$$
H(0)=4.8 \sin [\frac{\pi}{6}(3)]+5.1 \\
=4.8 \sin \frac{\pi}{2}+5.1 \\
=4.8 (1)+5.1 =9.9
$$
بزرگترین مقدار سینوس در \(\frac{\pi}{2}\) رخ می دهد، بنابراین معنادار است که بگوییم بلندترین جزر و مد زمانی خواهد بود که این فرمول از سینوس آن مقدار استفاده کند.
-
ارتفاع را تعیین کنید.
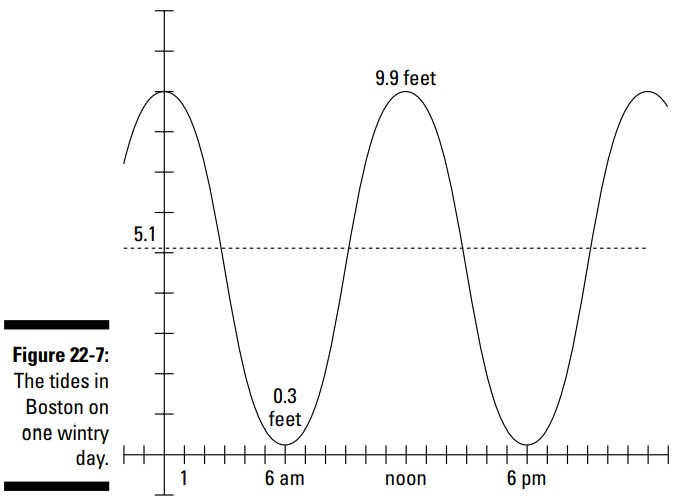
ضریب \(4.8\) دامنۀ نوسان می باشد ـــ این نمودار چقدر بالا و پایین مقدار میانی می رود. جزر و مدها \(4.8\) فوت بالا و پایین مقدار میانگین در این روز خاص می روند. عددی که در انتها اضافه شده است، یعنی \(5.1\)، میانگین ارتفاع جزر و مدها می باشد. بنابراین، این جزر و مدها تا \(9.9\) فوت بالا و تا \(0.3\) فوت پایین می روند.
-
دورۀ تناوب این تابع را بیابید.
ضریب \(\frac{\pi}{6}\) بر روی دورۀ تناوب اثر می گذارد. دورۀ تناوب تابع سینوس معمولاً برابر با \(2\pi\) می باشد. \(2\pi\) را بر \(\frac{\pi}{6}\) تقسیم کنید و به نتیجۀ زیر می رسید:
$$2\pi \div \frac{\pi}{6} = 2\pi \cdot \frac{6}{\pi} = 12$$
این دورۀ تناوب برابر با \(12\) ساعت می باشد، بنابراین شما می دانید که جزر و مدها در طول \(12\) ساعت از ابتدا تا انتهای دورۀ تناوبشان را طی می کنند. \(3\) که به \(t\) اضافه شده است یک انتقال افقی می باشد؛ این عدد نشان می دهد چه زمانی از روز بلندترین و کوتاهترین جزر و مد رخ می دهند. شکل 7-22 نموداری از این تابع و مراحل گوناگون جزر و مد در زمانهای مختلف را نشان می دهد. با مشاهدۀ این نمودار، شما می توانید فعالیت های قایقرانی و درآوردن صدف از زیر ماسه ها را برنامه ریزی کنید.
رصد کردن جمعیت گوزن ها
نمودار این بخش جمعیت یک گله گوزن را از اول آوریل تا آوریل سال بعد، نشان می دهد. گوزن های جدید در بهار متولد می شوند، بنابراین افزایش در اندازۀ گله انتظار می رود. شکارچیان (درندگان) به دنبال گوزن های ضعیفند ـــ هم جوان و هم پیر. و سپس شما باید آب و هوا را در نظر بگیرید؛ زمستان می تواند برای این جمعیت بسیار سخت باشد. به نمودار موجود در شکل 8-22 بنگرید و بررسی کنید که آیا آن چیزی را که انتظارش را داشتید، نشان می دهد یا خیر. این چرخه نتیجۀ یافتن مجموع دو تابع سینوس مختلف می باشد:
$$D(m)=400+40 \sin (0.524m)+20 \sin (1.047m)$$
این تابع نشان دهندۀ جمعیت گله می باشد، در این تابع \(m\) تعداد ماهها از آوریل می باشد.

این گله بالاترین تعداد یعنی \(450\) گوزن را در ژوئن و کمترین تعداد یعنی \(350\) گوزن را در فوریه، تجربه می کند. این مدل گله ای را نشان می دهد که تقریباً از سالی به سال دیگر اندازه اش یکسان باقی می ماند.
اندازه گیری جنبش یک شیء متصل به یک فنر
در این بخش، یک تابع مثلثاتی مدلی را برای یک شیء متصل به یک فنر اثبات می کند. مشابه بخشهای قبلی، الگوی یکسانی بارها و بارها تکرار نمی شود. اما این یک مثال عالی از یک تابع مثلثاتی در عمل می باشد.
معادلۀ \(H(t)=3(0.7)^t \cos 5t+4\) نشان دهندۀ ارتفاع یک شیء متصل به یک فنر می باشد، که در آن \(t\) نشان دهندۀ مقدار زمانی است که گذشته است ـــ معمولاً در واحد ثانیه. این معادله یک تابع مثلثاتی دارد که در یک تابع نمایی ضرب شده است. هنگامی که در ابتدا این فنر را رها می کنید، این شیء به ارتفاعی حدود \(7\) فوت می رسد. آن شیء بالا و پایین می جهد، سرانجام در حدود ارتفاع \(4\) فوتی آرام می گیرد، شکل 9-22 این امر را نشان می دهد.

شما احتمالاً با مدلی مشابه این مدل در هنگام نشان دادن بالا و پایین رفتن فردی که بانجی جامپینگ می کند، مواجه شوید. بنابراین، می توانید ببینید که توابع مثلثاتی انواع مختلف کاربردها را دارند ـــ بسیاری از این کاربردها خیلی سودمند هستند.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: