خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
محاسبات شکل های عجیب و مانور دادن روی گوشه ها

گاهی اوقات، یافتن یک اندازه به این آسانی ها نیست. شما ممکن است مجبور شوید با یک شکل نامنظم سر و کار داشته باشید یا حتی مسیرتان را پیرامون یک شیء ثابت محاسبه کنید. مورد هر کدام از اینها باشد، شما می توانید از مثلثات برای یافتن پاسخهایی که بدنبالش هستید، استفاده کنید.

رایج ترین فرمول برای مساحت یک مثلث \(A=\frac{1}{2}bh\) می باشد، که در آن \(A\) مساحت، \(b\) طول قاعدۀ مثلث، و \(h\) ارتفاع مثلث که به صورت عمود بر قاعدۀ آن ترسیم شده است، می باشند. شکل 11-10 اجزاء مختلف این فرمول را تشریح می کند.
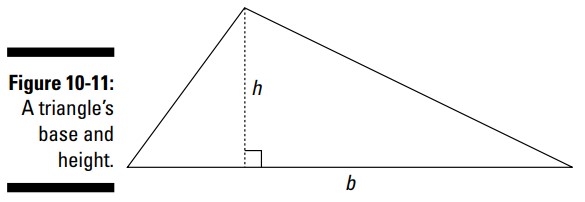
اگر شما بتوانید اندازۀ قاعده و ارتفاع را بدست آورید، و اگر بتوانید مطمئن شوید که ارتفاع بر آن ضلع مثلث عمود می باشد، این فرمول مساحت بخوبی کار می کند. اما اگر یک حیاط مثلثی شکل داشته باشید ـــ یک حیاط مثلثی شکل بزرگ ـــ و هیچ روشی برای اندازه گیری یک پاره خط خاص که بر یکی از اضلاع آن عمود باشد، نداشته باشید، در آن صورت چه می شود؟ یک روش جایگزین استفاده از فرمول هرون (Heron’s Formula) می باشد، که از اندازه های هر سه ضلع استفاده می کند. (در بخش بعدی فرمول هرون را در عمل به شما نشان خواهم داد.) جایگزین دیگر، مسلماً، استفاده از مثلثات می باشد ـــ یا دست کم، یک فرمول که در آن یک اندازۀ زاویه موجود باشد. برای اندازه گیری آن زاویه، شما می توانید بسیار پیشرفته عمل کنید و یک دستگاه نقشه برداری (surveying apparatus) تهیه کنید، و یا اگر یک زاویه سنج دستی دارید، می توانید از آن استفاده نمایید.
فرمول مثلثاتی برای یافتن مساحت یک مثلث \(A=\frac{1}{2}ab \sin \theta\) می باشد، که در آن \(a\) و \(b\) دو ضلع از این مثلث و زاویۀ \(\theta\) ، زاویۀ شکل گرفته بین آن دو ضلع می باشد. در این فرمول به هیچ وجه نیازی به اندازۀ ضلع سوم ندارید، و قطعاً نیازی هم به یک ضلع عمود ندارید.
با استفاده از مثلثات، من به شما نشان می دهم که این فرمول از کجا آمده است. نگاهی به مثلث موجود درشکل 12-10 که دارای اضلاع \(a\) و \(b\) و زاویۀ بین آنها می باشد، بیندازید.
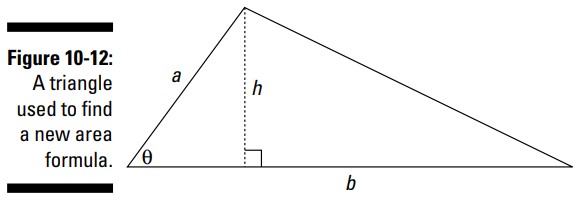
با فرمول سنتی برای مساحت این مثلث، کار را آغاز کنید، \(A=\frac{1}{2}ba\). سپس، آن مثلث کوچک سمت چپ را بررسی کنید. (از آنجا که ارتفاع آن بر قاعده عمود می باشد، این اضلاع و ارتفاع یک مثلث قائم الزاویه را تشکیل می دهند.) زاویۀ حادۀ \(\theta\) دارای سینوسی معادلِ \(\sin \theta = \frac{\text{opposite}}{\text{hypotenuse}} = \frac{h}{a}\) می باشد. اگر این معادله را برای بدست آوردن \(h\) حل کنید، خواهید داشت:
$$
\sin \theta = \frac{h}{a} \\
a \sin \theta = h
$$
اکنون در فرمول سنتی \(h\) را با معادل آن در فرمول بالا، جایگزین کنید، و خواهید داشت:
$$A=\frac{1}{2}bh=\frac{1}{2}b(a \sin \theta) = \frac{1}{2}ab \sin \theta$$
بررسی کنید این فرمول در یک مسالۀ واقعی چگونه کار می کند. در مثلث موجود در شکل 13-10 اندازۀ دو ضلع و زاویۀ بین آنها نشان داده شده است.
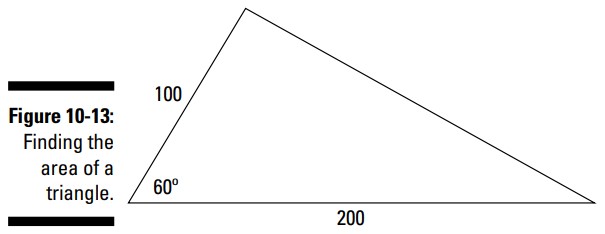
برای یافتن مساحت مثلث موجود در شکل 13-10:
همانطور که اندکی پیش در همین بخش به شما قول دادم، به شما نشان خواهم داد که چگونه با استفاده از فرمول هرون مساحت یک مثلث را بدست آوردید. فرمول هرون به ویژه در جاهایی سودمند است که شما به اندازۀ سه ضلع یک مثلث دسترسی داشته باشید اما نتوانید یک ارتفاع عمود برای آن ترسیم کنید یا زاویه سنجی برای اندازه گیری یکی از زوایای آن در اختیار نداشته باشید.
وضعیتی را در نظر بگیرید که در آن شما یک توپ بزرگ نخ داشته باشید که \(100\) یارد طول دارد و به شما گفته شده است که یک ناحیۀ مثلثی شکل را نشانه گذاری کنید ـــ و از این توپ نخ برای نشانه گذاری مرزهای این ناحیه استفاده کنید. شما \(40\) یارد را در یک جهت پیش می روید، می چرخید، و \(25\) یارد دیگر پیش می روید؛ سپس به محلی که از آنجا آغاز کرده بودید باز می گردید و در مسیر بازگشت آن \(35\) یارد باقی ماندۀ این توپ نخ را نیز مصرف می کنید. مساحتی که ایجاد کرده اید، چقدر است؟
فرمول هرون اینست:
$$A=\sqrt{s(s-a)(s-b)(s-c)}$$
در این فرمول \(a\) و \(b\) و \(c\) طول اضلاع این مثلث هستند و \(s\) مخفف semi-perimeter به معنای نصف محیط می باشد.
در مورد این مثلث، محیط برابر با \(40+25+35=100\) یارد می باشد. نصف آن \(50\) می شود، بنابراین فرمول به شکل زیر خواهد بود:
$$
A=\sqrt{50(50-40)(50-25)(50-35)} \\
= \sqrt{50(10)(25)(15)} = \sqrt{187,500} \approx 433
$$
ناحیۀ مثلثی شکلی که با این توپ نخ، نشانه گذاری کرده اید در حدود \(433\) یارد مربع می باشد.
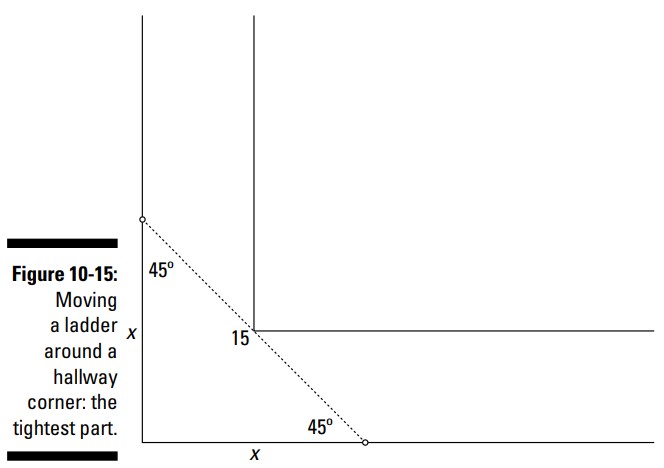
در اینجا کاربردی از مثلثات را داریم که شما ممکن است بخوبی قادر به ارتباط برقرار کردن با آن باشید: آیا تابحال سعی کرده اید یک تکۀ بزرگ از اثاثیه منزل را در داخل خانه جابجا کنید؟ شما آن را می چرخانید و سر و ته می کنید اما موفقیتی حاصل نمی شود. در این مثال، وانمود کنید که سعی دارید یک نردبان \(15\) فوتی را به گوشه ای از منزل ببرید که دو راهروی دارای عرض \(4\) فوت در یک زاویۀ \(90\) درجه به یکدیگر برخورد کرده اند. شکل 14-10 تصویری از این وضعیت را به شما نشان می دهد.
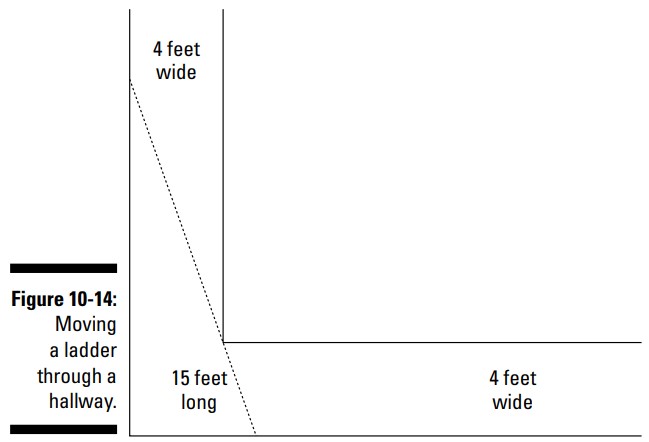
تنگ ترین قسمت زمانی است که نردبان در نیمۀ این راهرو است، یا زمانی است که زوایایی که دو دیوار بیرونی را لمس می کنند یکسان می باشند. هنگامیکه این نردبان در تنگ ترین نقطه قرار دارد، یک مثلث قائم الزاویه با اضلاع مساوی را تشکیل می دهد ـــ نیمی از نردبان در هر سمت از این گوشه قرار دارد. از آنجا که اضلاع این مثلث قائم الزاویه در این نقطه با هم برابرند، شما یک مثلث قائم الزاویۀ متساوی الساقین (isosceles right triangle) بدست می آورید، که دارای دو زاویۀ \(45\) درجه می باشد (شکل 15-10 را ببینید). در این حالت طول اضلاع این مثلث قائم الزوایه چقدر می باشند؟ هنگامی که ابعاد این مثلث قائم الزوایۀ متساوی الساقین را بدانید، می توانید وتر را بررسی کنید (وتر در اینجا نردبان می باشد) و تعیین کنید آیا به اندازۀ کافی کوتاه است که در تنگ ترین بخش این گوشه جا شود، یا اینکه بسیار بلند است. و مسلماً شما نمی خواهید دیوار را بخراشید یا در آن سوراخهایی را ایجاد کنید!

یافتن مساحت یک قطعه زمین مثلثی شکل
رایج ترین فرمول برای مساحت یک مثلث \(A=\frac{1}{2}bh\) می باشد، که در آن \(A\) مساحت، \(b\) طول قاعدۀ مثلث، و \(h\) ارتفاع مثلث که به صورت عمود بر قاعدۀ آن ترسیم شده است، می باشند. شکل 11-10 اجزاء مختلف این فرمول را تشریح می کند.

اگر شما بتوانید اندازۀ قاعده و ارتفاع را بدست آورید، و اگر بتوانید مطمئن شوید که ارتفاع بر آن ضلع مثلث عمود می باشد، این فرمول مساحت بخوبی کار می کند. اما اگر یک حیاط مثلثی شکل داشته باشید ـــ یک حیاط مثلثی شکل بزرگ ـــ و هیچ روشی برای اندازه گیری یک پاره خط خاص که بر یکی از اضلاع آن عمود باشد، نداشته باشید، در آن صورت چه می شود؟ یک روش جایگزین استفاده از فرمول هرون (Heron’s Formula) می باشد، که از اندازه های هر سه ضلع استفاده می کند. (در بخش بعدی فرمول هرون را در عمل به شما نشان خواهم داد.) جایگزین دیگر، مسلماً، استفاده از مثلثات می باشد ـــ یا دست کم، یک فرمول که در آن یک اندازۀ زاویه موجود باشد. برای اندازه گیری آن زاویه، شما می توانید بسیار پیشرفته عمل کنید و یک دستگاه نقشه برداری (surveying apparatus) تهیه کنید، و یا اگر یک زاویه سنج دستی دارید، می توانید از آن استفاده نمایید.
فرمول مثلثاتی برای یافتن مساحت یک مثلث \(A=\frac{1}{2}ab \sin \theta\) می باشد، که در آن \(a\) و \(b\) دو ضلع از این مثلث و زاویۀ \(\theta\) ، زاویۀ شکل گرفته بین آن دو ضلع می باشد. در این فرمول به هیچ وجه نیازی به اندازۀ ضلع سوم ندارید، و قطعاً نیازی هم به یک ضلع عمود ندارید.
با استفاده از مثلثات، من به شما نشان می دهم که این فرمول از کجا آمده است. نگاهی به مثلث موجود درشکل 12-10 که دارای اضلاع \(a\) و \(b\) و زاویۀ بین آنها می باشد، بیندازید.

با فرمول سنتی برای مساحت این مثلث، کار را آغاز کنید، \(A=\frac{1}{2}ba\). سپس، آن مثلث کوچک سمت چپ را بررسی کنید. (از آنجا که ارتفاع آن بر قاعده عمود می باشد، این اضلاع و ارتفاع یک مثلث قائم الزاویه را تشکیل می دهند.) زاویۀ حادۀ \(\theta\) دارای سینوسی معادلِ \(\sin \theta = \frac{\text{opposite}}{\text{hypotenuse}} = \frac{h}{a}\) می باشد. اگر این معادله را برای بدست آوردن \(h\) حل کنید، خواهید داشت:
$$
\sin \theta = \frac{h}{a} \\
a \sin \theta = h
$$
اکنون در فرمول سنتی \(h\) را با معادل آن در فرمول بالا، جایگزین کنید، و خواهید داشت:
$$A=\frac{1}{2}bh=\frac{1}{2}b(a \sin \theta) = \frac{1}{2}ab \sin \theta$$
بررسی کنید این فرمول در یک مسالۀ واقعی چگونه کار می کند. در مثلث موجود در شکل 13-10 اندازۀ دو ضلع و زاویۀ بین آنها نشان داده شده است.

برای یافتن مساحت مثلث موجود در شکل 13-10:
-
از فرمول \(A=\frac{1}{2}ab \sin \theta\) استفاده کنید، و مقادیر معلوم را در آن جایگذاری کنید.
$$A=\frac{1}{2}(100)(200)\sin 60^{\circ}$$
-
این معادله را برای بدست آوردن مقدار مساحت حل کنید.
$$
=\frac{1}{2}(100)(200) \cdot \frac{\sqrt{3}}{2} \\
=10,000 \cdot \frac{\sqrt{3}}{2} \approx 8,660
$$
مساحت این مثلث در حدود \(8,660\) واحد مربع می باشد.
استفاده از فرمول هرون (Heron’s Formula)
همانطور که اندکی پیش در همین بخش به شما قول دادم، به شما نشان خواهم داد که چگونه با استفاده از فرمول هرون مساحت یک مثلث را بدست آوردید. فرمول هرون به ویژه در جاهایی سودمند است که شما به اندازۀ سه ضلع یک مثلث دسترسی داشته باشید اما نتوانید یک ارتفاع عمود برای آن ترسیم کنید یا زاویه سنجی برای اندازه گیری یکی از زوایای آن در اختیار نداشته باشید.
وضعیتی را در نظر بگیرید که در آن شما یک توپ بزرگ نخ داشته باشید که \(100\) یارد طول دارد و به شما گفته شده است که یک ناحیۀ مثلثی شکل را نشانه گذاری کنید ـــ و از این توپ نخ برای نشانه گذاری مرزهای این ناحیه استفاده کنید. شما \(40\) یارد را در یک جهت پیش می روید، می چرخید، و \(25\) یارد دیگر پیش می روید؛ سپس به محلی که از آنجا آغاز کرده بودید باز می گردید و در مسیر بازگشت آن \(35\) یارد باقی ماندۀ این توپ نخ را نیز مصرف می کنید. مساحتی که ایجاد کرده اید، چقدر است؟
فرمول هرون اینست:
$$A=\sqrt{s(s-a)(s-b)(s-c)}$$
در این فرمول \(a\) و \(b\) و \(c\) طول اضلاع این مثلث هستند و \(s\) مخفف semi-perimeter به معنای نصف محیط می باشد.
در مورد این مثلث، محیط برابر با \(40+25+35=100\) یارد می باشد. نصف آن \(50\) می شود، بنابراین فرمول به شکل زیر خواهد بود:
$$
A=\sqrt{50(50-40)(50-25)(50-35)} \\
= \sqrt{50(10)(25)(15)} = \sqrt{187,500} \approx 433
$$
ناحیۀ مثلثی شکلی که با این توپ نخ، نشانه گذاری کرده اید در حدود \(433\) یارد مربع می باشد.
انتقال یک شیء به یک گوشه
در اینجا کاربردی از مثلثات را داریم که شما ممکن است بخوبی قادر به ارتباط برقرار کردن با آن باشید: آیا تابحال سعی کرده اید یک تکۀ بزرگ از اثاثیه منزل را در داخل خانه جابجا کنید؟ شما آن را می چرخانید و سر و ته می کنید اما موفقیتی حاصل نمی شود. در این مثال، وانمود کنید که سعی دارید یک نردبان \(15\) فوتی را به گوشه ای از منزل ببرید که دو راهروی دارای عرض \(4\) فوت در یک زاویۀ \(90\) درجه به یکدیگر برخورد کرده اند. شکل 14-10 تصویری از این وضعیت را به شما نشان می دهد.

تنگ ترین قسمت زمانی است که نردبان در نیمۀ این راهرو است، یا زمانی است که زوایایی که دو دیوار بیرونی را لمس می کنند یکسان می باشند. هنگامیکه این نردبان در تنگ ترین نقطه قرار دارد، یک مثلث قائم الزاویه با اضلاع مساوی را تشکیل می دهد ـــ نیمی از نردبان در هر سمت از این گوشه قرار دارد. از آنجا که اضلاع این مثلث قائم الزاویه در این نقطه با هم برابرند، شما یک مثلث قائم الزاویۀ متساوی الساقین (isosceles right triangle) بدست می آورید، که دارای دو زاویۀ \(45\) درجه می باشد (شکل 15-10 را ببینید). در این حالت طول اضلاع این مثلث قائم الزوایه چقدر می باشند؟ هنگامی که ابعاد این مثلث قائم الزوایۀ متساوی الساقین را بدانید، می توانید وتر را بررسی کنید (وتر در اینجا نردبان می باشد) و تعیین کنید آیا به اندازۀ کافی کوتاه است که در تنگ ترین بخش این گوشه جا شود، یا اینکه بسیار بلند است. و مسلماً شما نمی خواهید دیوار را بخراشید یا در آن سوراخهایی را ایجاد کنید!

-
تابع مثلثاتی ای را که می توانید با اندازه های موجود مورد استفاده قرار دهید، تعیین کنید.
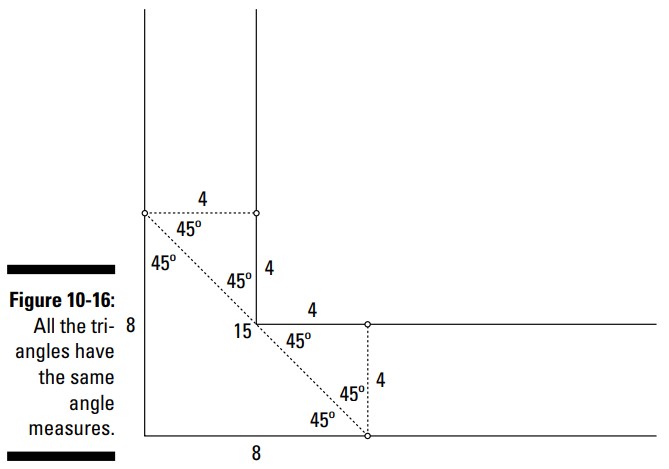
وتر برابر با طول نردبان یعنی \(15\) فوت می باشد. اضلاع روبرو و مجاور در یک مثلث قائم الزاویۀ متساوی الساقین هم اندازه می باشند، و در این مورد، آن دو طول هر کدام برابر با \(8\) فوت می باشند. شما این اندازه را از آنجا می دانید که تمامی این مثلثها قائم الزاویۀ متساوی الساقین می باشند، که بدین معناست که دارای زوایای \(45\) درجه و ساق های هم اندازه می باشند (شکل 16-10 را ببینید).
-
تعیین کنید که از کدام تابع مثلثاتی باید استفاده کنید.
هم سینوس و هم کسینوس شامل طول وتر می باشند، که چیزی است که می خواهید بدست آورید، بنابراین می توانید از هر کدام از این دو تابع استفاده کنید.
-
معادله ای با آن تابع مثلثاتی بنویسید؛ سپس مقادیر معلوم را در آن وارد کنید.
$$\sin 45 = \frac{\text{opposite}}{\text{hypotenuse}}=\frac{8}{\text{hypotenuse}}$$
-
این معادله را برای بدست آوردن مقدار وتر حل کنید.
$$
\frac{\sqrt{2}}{2}=\frac{8}{\text{hypotenuse}} \\
\sqrt{2} \cdot \text{hypotenuse} = 8.2 \\
\text{hypotenuse} = \frac{16}{\sqrt{2}} \\
\approx 11.314
$$
شما دریافتید که در تنگ ترین نقطه پیرامون این گوشه، وتر صرفاً اندکی بیش از \(11\) فوت می باشد. این نردبان \(15\) فوتی هرگز در آن گوشه جا نخواهد شد.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: