خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
تابع جذر (ریشۀ مربع) (square root function)

مساحت یک مربع (square) با مربع کردن ضلع آن بدست می آید. اگر y مساحت یک مربع باشد و x طول یک ضلع آن باشد، سپس با این فرمول می توانید مساحت آن مربع را بدست آورید: \(y=x^2\)

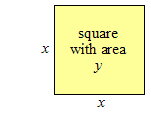
اگر طول \(x\) را داشته باشیم و بخواهیم مساحت \(y\) را بدست آوریم، این فرمول خوب است، اما اگر مساحت \(y\) را داشته باشیم و بخواهیم طول \(x\) را بیابیم چه می شود؟ خوب، ابتدا به این طول مجهول یک نام می دهیم. ما آن را ریشۀ مربع (square root) می نامیم (معنای واقعی آن می شود، پاسخ مسألۀ مربع: ریشه (root) در ریاضیات معنای پاسخ می دهد). سپس یک تابع ریشۀ مربع می سازیم تا آن را محاسبه کنیم. ورودی این تابع مساحت مربع مورد نظر و خروجی آن طول یک ضلع مربع می باشد.
در اینجا یک تعریف رسمی از تابع ریشۀ مربع (جذر) داریم:
مثال 1: مقدار \(\sqrt{16}\) را ارزیابی کنید.
آرگومان \(16\)، از این تابع ریشۀ مربع (جذر) را می توان به سادگی به شکل \(4^2\) نشان داد، بنابراین تابع ریشۀ مربع، مقدار \(4\) را باز می گرداند.
$$
\sqrt{16}=\sqrt{4^2}=4
$$
مثال 2: مقدار \(\sqrt{5.7^2}\) را ارزیابی کنید.
در این مثال، آرگومان تابع جذر هم اکنون به شکل عددی مربع نمایش داده شده است، بنابراین تابع جذر به سادگی فقط آن عدد را بر می گرداند.
$$
\sqrt{5.7^2}=5.7
$$
مثال 3: مقدار \(\sqrt{24.6016}\) را ارزیابی کنید.
در این مثال، آرگومان تابع، عددی است که ما نمی دانیم چگونه آن را باید به شکل مربع عدد دیگری نشان بدهیم. بنابراین از یک ماشین حساب برای محاسبۀ آن استفاده می کنیم.
$$
\sqrt{24.6016}=4.96
$$
در اینجا نمودار تابع ریشۀ مربع را می بینید.
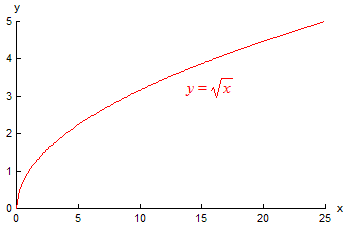
دامنه و برد تابع جذر: دامنۀ تابع جذر، عبارت از تمامی اعداد حقیقی غیرمنفی (مثبت) می باشد و بُرد آن نیز شامل تمامی اعداد حقیقی غیرمنفی (مثبت) می باشد.
تابع مربع (square function)، معکوس تابع ریشۀ مربع (square root function) می باشد. با این حال در نظر داشته باشید که تابع ریشۀ مربع فقط زمانی معکوس تابع مربع است که دامنۀ تابع مربع به اعداد مثبت محدود شده باشند.
تابع ریشۀ مربع یک تابع یک به یک (one-to-one function) است، که یک عدد غیرمنفی را می گیرد و ریشۀ مربع آن عدد را به عنوان خروجی باز می گرداند. به عنوان مثال، عدد \(9\) به عدد \(3\) متناظر می شود.

تابع مربع، هر عددی (مثبت یا منفی) را به عنوان ورودی می گیرد و مربع آن عدد را به عنوان خروجی باز می گرداند. برای مثال، عدد \(3\) به عدد \(9\) متناظر می شود. از آنجا که تابع مربع، عدد اصلی را به ما باز می گرداند، پس معکوس تابع ریشۀ مربع می باشد.
با این حال تابع مربع یک تابع چند به یک (many-to-one function) می باشد. برای مثال، هم عدد \(3\) و هم عدد \(-3\) به عدد \(9\) متناظر می شوند.
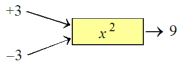
از این رو، تابع مربع، معکوس ندارد. اگر چنین شود، تناظر آن به شکل یک به چند (one-to-many) خواهد بود و اساساً دیگر یک تابع نخواهد بود. این بدین معناست که، رابطۀ زیر به ازاء هر \(x\) برقرار است:
$$
\biggl( \sqrt{x} \biggr)^2 = x
$$
اما رابطۀ زیر اینگونه نیست:
$$
\sqrt{x^2} \ne x
$$
مگر اینکه \(x\) عددی مثبت باشد، به دو مثال زیر توجه کنید:
$$
\sqrt{(3)^2} = 3 \\
\sqrt{(-3)^2} \ne -3
$$
فرض کنید که \(x\) مجهول باشد اما \(x^2\) برابر با مقدار معلوم \(y\) باشد. آن گاه یافتن \(x\) مستلزم اینست که معادلۀ زیر را برای بدست آوردن \(x\) حل کنید.
$$
x^2 = y
$$
در اینجا دو پاسخ خواهیم داشت. یک پاسخ برابر است با:
$$
x=\sqrt{y}
$$
در اینجا یک پاسخ دومی هم داریم:
$$
x=-\sqrt{y}
$$
معمولاً این دو پاسخ با استفاده از علامت \(\pm\) در کنار یکدیگر قرار داده می شوند و اینگونه بیان می شوند:
$$
x=\pm \sqrt{y}
$$
مثال 1: پاسخ معادلۀ \(x^2 = 16\) برابر با \(x=\pm 4\) می باشد.
مثال 2: پاسخ معادلۀ \(x^2 = 5.7^2\) برابر با \(x = \pm 5.7\) می باشد.
مثال 3: پاسخ معادلۀ \(x^2 = -16\) عدد موهومی \(x=\pm 5.7 i\) می باشد.
مثال 4: پاسخ معادلۀ \(x^2=-(5.7^2)\) عدد موهومی \(x = \pm 5.7i\) می باشد.

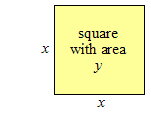
اگر طول \(x\) را داشته باشیم و بخواهیم مساحت \(y\) را بدست آوریم، این فرمول خوب است، اما اگر مساحت \(y\) را داشته باشیم و بخواهیم طول \(x\) را بیابیم چه می شود؟ خوب، ابتدا به این طول مجهول یک نام می دهیم. ما آن را ریشۀ مربع (square root) می نامیم (معنای واقعی آن می شود، پاسخ مسألۀ مربع: ریشه (root) در ریاضیات معنای پاسخ می دهد). سپس یک تابع ریشۀ مربع می سازیم تا آن را محاسبه کنیم. ورودی این تابع مساحت مربع مورد نظر و خروجی آن طول یک ضلع مربع می باشد.
در اینجا یک تعریف رسمی از تابع ریشۀ مربع (جذر) داریم:
تعریف: تابع ریشۀ دوم تعریف شده است تا هر عدد مثبت \(y\) را به عنوان ورودی بگیرد و عدد مثبت \(x\) را بازگرداند که باید مربع شده باشد (یعنی در خودش ضرب شده باشد)، تا \(y\) را نتیجه بدهد. ریشۀ مربع \(y\) معمولاً اینگونه نمایش داده می شود: \(\sqrt{y}\)
نماد \(\sqrt{}\) نماد رادیکال (radical symbol) نامیده می شود و مقدار داخل آن آرگومان (argument) ریشۀ دوم نامیده می شود. در برخی از کتابهای ریاضی این تابع را اینگونه نیز نشان می دهند: \(\sqrt{(y)}\).
نماد \(\sqrt{}\) نماد رادیکال (radical symbol) نامیده می شود و مقدار داخل آن آرگومان (argument) ریشۀ دوم نامیده می شود. در برخی از کتابهای ریاضی این تابع را اینگونه نیز نشان می دهند: \(\sqrt{(y)}\).
مثال 1: مقدار \(\sqrt{16}\) را ارزیابی کنید.
آرگومان \(16\)، از این تابع ریشۀ مربع (جذر) را می توان به سادگی به شکل \(4^2\) نشان داد، بنابراین تابع ریشۀ مربع، مقدار \(4\) را باز می گرداند.
$$
\sqrt{16}=\sqrt{4^2}=4
$$
مثال 2: مقدار \(\sqrt{5.7^2}\) را ارزیابی کنید.
در این مثال، آرگومان تابع جذر هم اکنون به شکل عددی مربع نمایش داده شده است، بنابراین تابع جذر به سادگی فقط آن عدد را بر می گرداند.
$$
\sqrt{5.7^2}=5.7
$$
مثال 3: مقدار \(\sqrt{24.6016}\) را ارزیابی کنید.
در این مثال، آرگومان تابع، عددی است که ما نمی دانیم چگونه آن را باید به شکل مربع عدد دیگری نشان بدهیم. بنابراین از یک ماشین حساب برای محاسبۀ آن استفاده می کنیم.
$$
\sqrt{24.6016}=4.96
$$
نمودار تابع ریشۀ مربع (جذر)
در اینجا نمودار تابع ریشۀ مربع را می بینید.

دامنه و برد تابع جذر: دامنۀ تابع جذر، عبارت از تمامی اعداد حقیقی غیرمنفی (مثبت) می باشد و بُرد آن نیز شامل تمامی اعداد حقیقی غیرمنفی (مثبت) می باشد.
\(\sqrt{x}\) و \(x^2\) توابع معکوس یکدیگر می باشند
تابع مربع (square function)، معکوس تابع ریشۀ مربع (square root function) می باشد. با این حال در نظر داشته باشید که تابع ریشۀ مربع فقط زمانی معکوس تابع مربع است که دامنۀ تابع مربع به اعداد مثبت محدود شده باشند.
تابع ریشۀ مربع یک تابع یک به یک (one-to-one function) است، که یک عدد غیرمنفی را می گیرد و ریشۀ مربع آن عدد را به عنوان خروجی باز می گرداند. به عنوان مثال، عدد \(9\) به عدد \(3\) متناظر می شود.

تابع مربع، هر عددی (مثبت یا منفی) را به عنوان ورودی می گیرد و مربع آن عدد را به عنوان خروجی باز می گرداند. برای مثال، عدد \(3\) به عدد \(9\) متناظر می شود. از آنجا که تابع مربع، عدد اصلی را به ما باز می گرداند، پس معکوس تابع ریشۀ مربع می باشد.
با این حال تابع مربع یک تابع چند به یک (many-to-one function) می باشد. برای مثال، هم عدد \(3\) و هم عدد \(-3\) به عدد \(9\) متناظر می شوند.

از این رو، تابع مربع، معکوس ندارد. اگر چنین شود، تناظر آن به شکل یک به چند (one-to-many) خواهد بود و اساساً دیگر یک تابع نخواهد بود. این بدین معناست که، رابطۀ زیر به ازاء هر \(x\) برقرار است:
$$
\biggl( \sqrt{x} \biggr)^2 = x
$$
اما رابطۀ زیر اینگونه نیست:
$$
\sqrt{x^2} \ne x
$$
مگر اینکه \(x\) عددی مثبت باشد، به دو مثال زیر توجه کنید:
$$
\sqrt{(3)^2} = 3 \\
\sqrt{(-3)^2} \ne -3
$$
حل کردن معادلۀ \(x^2 = y\) برای بدست آوردن \(x\)، با استفاده از تابع ریشۀ مربع
فرض کنید که \(x\) مجهول باشد اما \(x^2\) برابر با مقدار معلوم \(y\) باشد. آن گاه یافتن \(x\) مستلزم اینست که معادلۀ زیر را برای بدست آوردن \(x\) حل کنید.
$$
x^2 = y
$$
در اینجا دو پاسخ خواهیم داشت. یک پاسخ برابر است با:
$$
x=\sqrt{y}
$$
در اینجا یک پاسخ دومی هم داریم:
$$
x=-\sqrt{y}
$$
معمولاً این دو پاسخ با استفاده از علامت \(\pm\) در کنار یکدیگر قرار داده می شوند و اینگونه بیان می شوند:
$$
x=\pm \sqrt{y}
$$
مثال 1: پاسخ معادلۀ \(x^2 = 16\) برابر با \(x=\pm 4\) می باشد.
مثال 2: پاسخ معادلۀ \(x^2 = 5.7^2\) برابر با \(x = \pm 5.7\) می باشد.
مثال 3: پاسخ معادلۀ \(x^2 = -16\) عدد موهومی \(x=\pm 5.7 i\) می باشد.
مثال 4: پاسخ معادلۀ \(x^2=-(5.7^2)\) عدد موهومی \(x = \pm 5.7i\) می باشد.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: