خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
نمایش فرمول ها و معادلات با نمودار
یک نمودار جبری تصویری از ارتباط بین دو عدد می باشد که مختصات یک نقطه را شکل می دهند. ارتباط بین مختصات ممکن است در شکل یک معادله ساده همچون \(y=x+3\) بیاید، که بیان می دارد مختصات \(x\) هر چه که باشد، مختصات \(y\) از آن \(3\) واحد بزرگتر است. ارتباط یا معادله ای دیگر ممکن است بیان کند که مجموع مربع دو مختصات باید دقیقاً برابر با \(25\) گردد: \(x^2+y^2=25\) . ارتباطات بسیار و متنوعند. در این بخش چند مثال از نمودارهای معادلات و فرمول ها را به شما نشان می دهم.

نمودار (graph) یک معادله خطی دارای دو متغیر، یک خط می باشد. برای مثال، نمودار معادلۀ خطی \(y=x+3\) یک خط است که با افزایش مختصات \(x\) به شکل رو به بالا ظاهر می شود. در مورد خطها در فصل 20 بیشتر صحبت خواهم کرد. فعلاً، قصدم اینست که صرفاً به شما چگونگی ترسیم یک نمودار ساده را نشان بدهم.
نمودار \(y=x+3\) از ابتدا تا انتهای تمامی نقاطی در صفحه مختصات که این معادله را یک گزاره صحیح می کنند، حرکت می کند. برای مثال، اگر \(x=2\) ، سپس \(y=2+3=5\) ، و شما نقطه \( (2,5) \) را خواهید داشت. در اینجا برخی از نقاطی که این معادله را گزاره ای صحیح می کنند می بینید:
$$
\begin{array}{|c|c|c|c|} \hline
(–4, –1) & (–3, 0) & (–2, 1) & (–1, 2) \\ \hline
(0, 3) & (1, 4) & (2, 5) & (3, 6) \\ \hline
\end{array}
$$
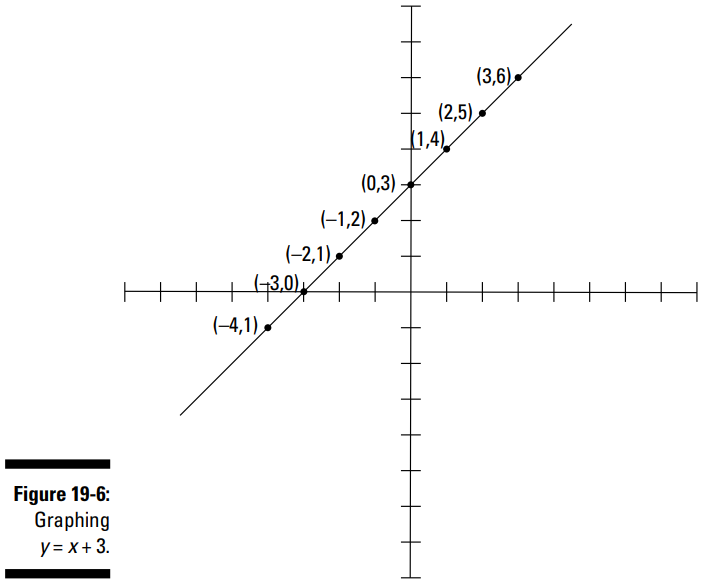
تعداد نقاطی که معادله را برآورده می کنند بی نهایت فراوان هستند. شما برای ترسیم نمودار قابل قبول فقط به چند تا از این نقاط نیاز دارید. (در حقیقت، شما فقط با داشتن دو نقطه می توانید خطی را ترسیم کنید، اما من به منظور صحت بیش از دو نقطه را ترسیم می کنم.) شکل 6-19 نقاط ترسیم شده و به یکدیگر متصل شده را به شما نشان می دهد.
مثالی از یک معادله با نمودار دایره شکل \(x^2+y^2=25\) می باشد. دایره ای که این معادله را نشان می دهد از میان بی نهایت نقطه عبور می کند. در اینجا فقط برخی از این نقاط آمده اند:
$$
\begin{array}{|c|c|c|c|c|c|} \hline
(0, 5) & (0, –5) & (5, 0) & (–5, 0) & (3, 4) & (–3, 4) \\ \hline
(4, 3) & (4, –3) & (–3,4) & (–3, –4) & (–4, –3) & \\ \hline
\end{array}
$$
من تمامی نقاط ممکن با مختصات اعداد صحیح را تمام نکرده ام، اجازه بدهید صرفاً یک نقطه را هم با مختصات کسری نشان بدهیم، مانند : \( \biggl( {25\over13},{60\over13} \biggr) \) .
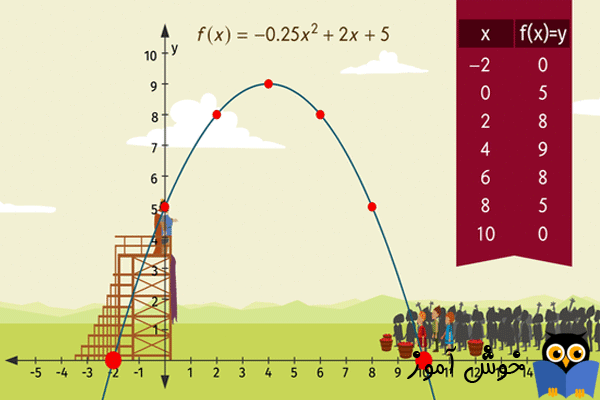
معادله ارتفاع یک شیء که به آسمان پرتاب شده است و سرعت اولیه آن \(v_0\) و ارتفاع اولیه آن \(h_0\) می باشد برابر با \(h(t)=-16t^2+v_0t+h_0\) است که در این معادله \(t\) مدت زمانی است که از زمان پرتاب آن شیء می گذرد. با جایگزین کردن \(t\) با \(x\) و \(h(t)\) با \(y\) ، می توانیم نمودار این معادله را در محورهای مختصات ترسیم کنیم.
مثال: یک توپ با سرعت اولیۀ \(132\) فوت در ثانیه (feet per second) به هوا پرتاب می شود. شخصی که این توپ را پرتاب کرده است بر روی ساختمانی با ارتفاع \(40\) فوت ایستاده است. بنابراین معادله ای که ارتفاع این توپ را نشان می دهد، عبارت از \( h(t)=-16t^2+132t+40 \) یا \( y=-16x^2+132x+40 \) می باشد. نمودار این معادله را ترسیم کنید.
ابتدا، برخی از نقاط را با قرار دادن مقادیری برای \(x\) محاسبه کنید. با \(0\) آغاز کنید و هر بار \(1\) واحد آن را افزایش بدهید، به نقاط زیر خواهید رسید:
$$
\begin{array}{|c|c|c|c|c|} \hline
(0, 40) & (1, 156)& (2, 240)& (3, 292) &(4, 312) \\ \hline
(5, 300)& (6, 256)& (7, 180) &(8, 72)& (9, –68) \\ \hline
\end{array}
$$
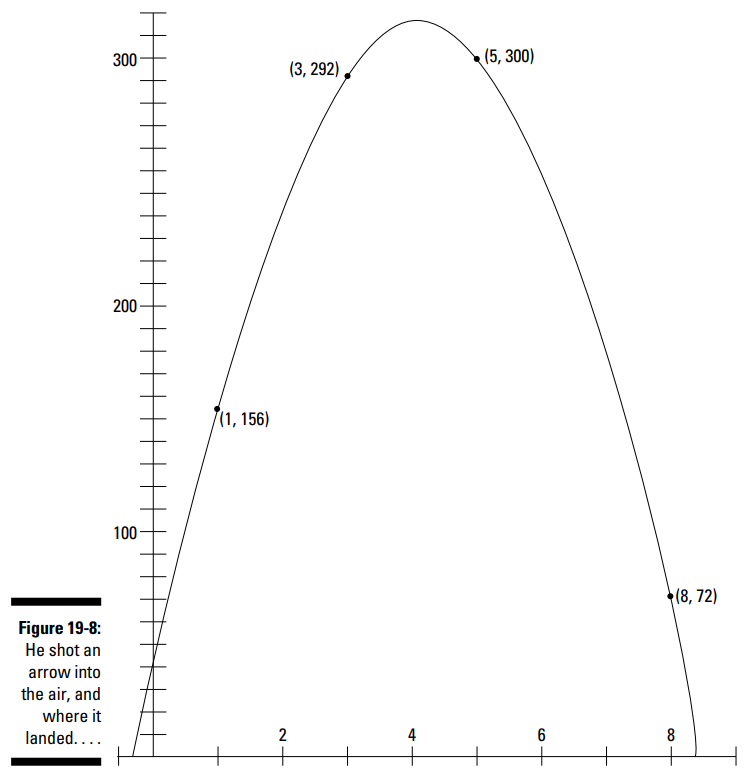
شکل 8-19 نمودار و برخی نقاط بر روی آن را به شما نشان می دهد.

نمودار معادله خطی (linear equation)
نمودار (graph) یک معادله خطی دارای دو متغیر، یک خط می باشد. برای مثال، نمودار معادلۀ خطی \(y=x+3\) یک خط است که با افزایش مختصات \(x\) به شکل رو به بالا ظاهر می شود. در مورد خطها در فصل 20 بیشتر صحبت خواهم کرد. فعلاً، قصدم اینست که صرفاً به شما چگونگی ترسیم یک نمودار ساده را نشان بدهم.
نمودار \(y=x+3\) از ابتدا تا انتهای تمامی نقاطی در صفحه مختصات که این معادله را یک گزاره صحیح می کنند، حرکت می کند. برای مثال، اگر \(x=2\) ، سپس \(y=2+3=5\) ، و شما نقطه \( (2,5) \) را خواهید داشت. در اینجا برخی از نقاطی که این معادله را گزاره ای صحیح می کنند می بینید:
$$
\begin{array}{|c|c|c|c|} \hline
(–4, –1) & (–3, 0) & (–2, 1) & (–1, 2) \\ \hline
(0, 3) & (1, 4) & (2, 5) & (3, 6) \\ \hline
\end{array}
$$
تعداد نقاطی که معادله را برآورده می کنند بی نهایت فراوان هستند. شما برای ترسیم نمودار قابل قبول فقط به چند تا از این نقاط نیاز دارید. (در حقیقت، شما فقط با داشتن دو نقطه می توانید خطی را ترسیم کنید، اما من به منظور صحت بیش از دو نقطه را ترسیم می کنم.) شکل 6-19 نقاط ترسیم شده و به یکدیگر متصل شده را به شما نشان می دهد.
معادله ای با نمودار دایره ای (circular graph)
مثالی از یک معادله با نمودار دایره شکل \(x^2+y^2=25\) می باشد. دایره ای که این معادله را نشان می دهد از میان بی نهایت نقطه عبور می کند. در اینجا فقط برخی از این نقاط آمده اند:
$$
\begin{array}{|c|c|c|c|c|c|} \hline
(0, 5) & (0, –5) & (5, 0) & (–5, 0) & (3, 4) & (–3, 4) \\ \hline
(4, 3) & (4, –3) & (–3,4) & (–3, –4) & (–4, –3) & \\ \hline
\end{array}
$$
من تمامی نقاط ممکن با مختصات اعداد صحیح را تمام نکرده ام، اجازه بدهید صرفاً یک نقطه را هم با مختصات کسری نشان بدهیم، مانند : \( \biggl( {25\over13},{60\over13} \biggr) \) .
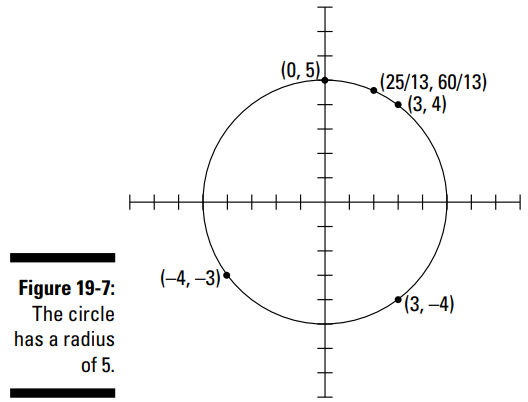
نکته: هنگام ترسیم نمودار برای یک معادله، انتظار نداشته باشید تمامی نقاط را بیابید. شما تنها می خواهید نقاط کافی را پیدا کنید تا به شما کمک کند جزئیات بیشتری در مورد سایر نقاط بدون اینکه نام آنها را بدانید، ارائه دهید.
در شکل 7-19 من نمودار دایره و برخی از نقاط دارای نام که نمودار دایره را ایجاد کرده اند، به شما نشان داده ام.پرتاب کردن یک شیء به هوا
معادله ارتفاع یک شیء که به آسمان پرتاب شده است و سرعت اولیه آن \(v_0\) و ارتفاع اولیه آن \(h_0\) می باشد برابر با \(h(t)=-16t^2+v_0t+h_0\) است که در این معادله \(t\) مدت زمانی است که از زمان پرتاب آن شیء می گذرد. با جایگزین کردن \(t\) با \(x\) و \(h(t)\) با \(y\) ، می توانیم نمودار این معادله را در محورهای مختصات ترسیم کنیم.
مثال: یک توپ با سرعت اولیۀ \(132\) فوت در ثانیه (feet per second) به هوا پرتاب می شود. شخصی که این توپ را پرتاب کرده است بر روی ساختمانی با ارتفاع \(40\) فوت ایستاده است. بنابراین معادله ای که ارتفاع این توپ را نشان می دهد، عبارت از \( h(t)=-16t^2+132t+40 \) یا \( y=-16x^2+132x+40 \) می باشد. نمودار این معادله را ترسیم کنید.
ابتدا، برخی از نقاط را با قرار دادن مقادیری برای \(x\) محاسبه کنید. با \(0\) آغاز کنید و هر بار \(1\) واحد آن را افزایش بدهید، به نقاط زیر خواهید رسید:
$$
\begin{array}{|c|c|c|c|c|} \hline
(0, 40) & (1, 156)& (2, 240)& (3, 292) &(4, 312) \\ \hline
(5, 300)& (6, 256)& (7, 180) &(8, 72)& (9, –68) \\ \hline
\end{array}
$$
شکل 8-19 نمودار و برخی نقاط بر روی آن را به شما نشان می دهد.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: