خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
ضد مشتق گیری (Antidifferentiation)

فصل 14 روش سخت محاسبۀ مساحت زیر یک تابع با استفاده از تعریف رسمی انتگرال ـــ حد جمع ریمان ـــ را به شما نشان داد. در این فصل، من مساحت ها را با روش ساده با بهره گیری از مزیت یکی از مهمترین و حیرت آورترین کشف های ریاضیات ـــ اینکه انتگرال گیری (یافتن مساحت ها) صرفاً برعکس مشتق گیری می باشد ـــ محاسبه می کنم. این فرآیند معکوس یک کشف بزرگ بود، و مبتنی بر چندین مفهوم مشکل می باشد، اما قبل از آنکه وارد آن شویم، بیایید در مورد یک فرآیند معکوس مرتبط و سرراست صحبت کنیم، یعنی ....

مشتق \(\sin x\) برابر با \(\cos x\) می باشد، بنابراین ضدمشتق \(\cos x\) برابر با \(\sin x\) می باشد؛ مشتق \(x^3\) برابر با \(3x^2\) می باشد، بنابراین ضدمشتق \(3x^2\) برابر با \(x^3\) می باشد ـــ شما صرفاً رو به عقب عمل می کنید. چیزهای بیشتری در مورد آن وجود دارد، اما مفهوم اصلی همین است. بعداً در این فصل، به شما نشان می دهم چگونه مساحت ها را با استفاده از ضد مشتق (antiderivative) بیابید. این بسیار ساده تر از یافتن مساحت ها با استفاده از تکنیک جمع ریمان می باشد.
اکنون دوباره \(x^3\) و مشتق آن \(3x^2\) را در نظر بگیرید. مشتق \(x^3 + 10\) نیز \(3x^2\) می باشد، همچنین مشتق \(x^3 - 5\). هر تابعی در شکل \(x^3+C\) که در آن \(C\) برابر با هر عددی باشد، دارای مشتق \(3x^2\) می باشد. بنابراین، هر تابع اینچنینی یک ضد مشتق \(3x^2\) دارد.
شما احتمالاً این نماد انتگرال، \(\int\)، را از بحث های انتگرال معین در فصل 14 می شناسید. اگرچه، نماد انتگرال معین، دارای دو عدد کوچک می باشد، مانند \(\int_4^{10}\) که به شما می گوید تا مساحت زیر یک تابع را بین آن دو عدد محاسبه کنید، که به آنها حدهای انتگرال گیری گفته می شود. نسخۀ برهنۀ این نماد، \(\int\)، یک انتگرال نامعین یا یک ضدمشتق را نشان می دهد. این فصل تماماً دربارۀ ارتباطات نزدیک بین این دو نماد و این دو مفهوم می باشد.
شکل 1-15 خانوادۀ ضدمشتق های \(3x^2\)، یعنی \(x^3+C\) را نشان می دهد. توجه داشته باشید که این خانواده از منحنی ها دارای بی نهایت منحنی می باشند. آنها تا ابد بالا و پایین می روند و دارای انبوه بی نهایت می باشند. شکاف عمودی \(2\) واحدی بین هر منحنی در شکل 1-15 صرفاً یک کمک کنندۀ بصری می باشد.
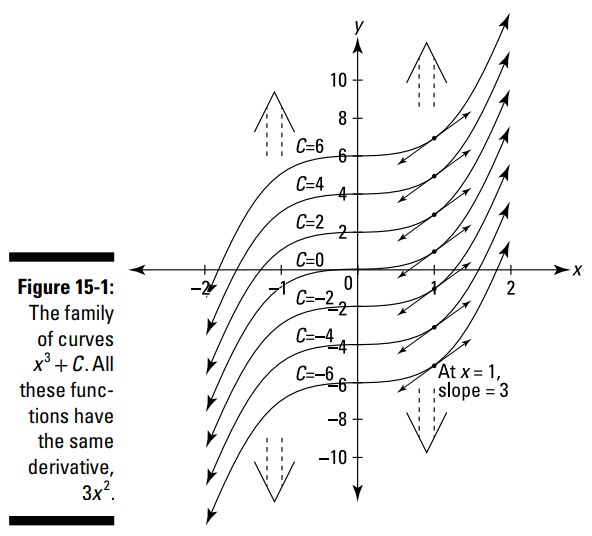
چندین چیز را دربارۀ شکل 1-15 در نظر بگیرید. منحنی بالا در این نمودار \(y=x^3+6\) می باشد؛ منحنی زیر آن برابر با \(y=x^3 +4\) می باشد؛ مورد پایینی برابر با \(y=x^3-6\) می باشد. با استفاده از قاعدۀ توان (Power rule)، این سه تابع، همانند تمامی توابع دیگر در این خانواده از توابع، دارای مشتق \(3x^2\) می باشند. اکنون، شیب هر کدام از این منحنی های را در جایی که \(x\) برابر با \(1\) باشد، در نظر بگیرید (خط مماس ترسیم شده بر روی منحنی ها را ببینید). مشتق هر تابع برابر با \(3x^2\) است، بنابراین وقتیکه \(x\) برابر با \(1\) باشد، شیب هر منحنی برابر با \(3 \cdot 1^2 = 3\) می باشد. بنابراین تمامی این خط های مماس کوچک با یکدیگر موازی می باشند. در ادامه، توجه داشته باشید که تمامی توابع موجود در شکل 1-15 یکسان هستند، با این استثناء که اندکی به بالا یا پایین لغزیده اند (جابجایی های عمودی از فصل 5 را به یاد دارید؟). از آنجا که آنها صرفاً با یک انتقال عمودی (vertical shift) با هم متفاوتند، شیب در هر مقدار \(x\)، همانند \(x=1\)، برای تمامی این منحنی ها یکسان است. این روش بصری برای اینست که درک کنید چرا هر کدام از این منحنی ها دارای مشتق یکسان می باشند، و بنابراین هر کدام از این منحنی ها ضدمشتقی از تابعی یکسان می باشند.

ضد مشتق گیری (Antidifferentiation)
مشتق \(\sin x\) برابر با \(\cos x\) می باشد، بنابراین ضدمشتق \(\cos x\) برابر با \(\sin x\) می باشد؛ مشتق \(x^3\) برابر با \(3x^2\) می باشد، بنابراین ضدمشتق \(3x^2\) برابر با \(x^3\) می باشد ـــ شما صرفاً رو به عقب عمل می کنید. چیزهای بیشتری در مورد آن وجود دارد، اما مفهوم اصلی همین است. بعداً در این فصل، به شما نشان می دهم چگونه مساحت ها را با استفاده از ضد مشتق (antiderivative) بیابید. این بسیار ساده تر از یافتن مساحت ها با استفاده از تکنیک جمع ریمان می باشد.
اکنون دوباره \(x^3\) و مشتق آن \(3x^2\) را در نظر بگیرید. مشتق \(x^3 + 10\) نیز \(3x^2\) می باشد، همچنین مشتق \(x^3 - 5\). هر تابعی در شکل \(x^3+C\) که در آن \(C\) برابر با هر عددی باشد، دارای مشتق \(3x^2\) می باشد. بنابراین، هر تابع اینچنینی یک ضد مشتق \(3x^2\) دارد.
تعریف انتگرال نامعین (indefinite integral): انتگرال نامعین تابع \(f(x)\)، که به شکل \(\int f(x)dx\) نوشته می شود، برابر با خانوادۀ تمامی ضدمشتق های آن تابع می باشد. به عنوان مثال، از آنجا که مشتق \(x^3\) برابر با \(3x^2\) است، انتگرال نامعین \(3x^2\) برابر با \(x^3 + C\) می باشد، و آن را اینگونه می نویسید:
$$\int 3x^2 dx = x^3 + C$$
$$\int 3x^2 dx = x^3 + C$$
شما احتمالاً این نماد انتگرال، \(\int\)، را از بحث های انتگرال معین در فصل 14 می شناسید. اگرچه، نماد انتگرال معین، دارای دو عدد کوچک می باشد، مانند \(\int_4^{10}\) که به شما می گوید تا مساحت زیر یک تابع را بین آن دو عدد محاسبه کنید، که به آنها حدهای انتگرال گیری گفته می شود. نسخۀ برهنۀ این نماد، \(\int\)، یک انتگرال نامعین یا یک ضدمشتق را نشان می دهد. این فصل تماماً دربارۀ ارتباطات نزدیک بین این دو نماد و این دو مفهوم می باشد.
شکل 1-15 خانوادۀ ضدمشتق های \(3x^2\)، یعنی \(x^3+C\) را نشان می دهد. توجه داشته باشید که این خانواده از منحنی ها دارای بی نهایت منحنی می باشند. آنها تا ابد بالا و پایین می روند و دارای انبوه بی نهایت می باشند. شکاف عمودی \(2\) واحدی بین هر منحنی در شکل 1-15 صرفاً یک کمک کنندۀ بصری می باشد.

چندین چیز را دربارۀ شکل 1-15 در نظر بگیرید. منحنی بالا در این نمودار \(y=x^3+6\) می باشد؛ منحنی زیر آن برابر با \(y=x^3 +4\) می باشد؛ مورد پایینی برابر با \(y=x^3-6\) می باشد. با استفاده از قاعدۀ توان (Power rule)، این سه تابع، همانند تمامی توابع دیگر در این خانواده از توابع، دارای مشتق \(3x^2\) می باشند. اکنون، شیب هر کدام از این منحنی های را در جایی که \(x\) برابر با \(1\) باشد، در نظر بگیرید (خط مماس ترسیم شده بر روی منحنی ها را ببینید). مشتق هر تابع برابر با \(3x^2\) است، بنابراین وقتیکه \(x\) برابر با \(1\) باشد، شیب هر منحنی برابر با \(3 \cdot 1^2 = 3\) می باشد. بنابراین تمامی این خط های مماس کوچک با یکدیگر موازی می باشند. در ادامه، توجه داشته باشید که تمامی توابع موجود در شکل 1-15 یکسان هستند، با این استثناء که اندکی به بالا یا پایین لغزیده اند (جابجایی های عمودی از فصل 5 را به یاد دارید؟). از آنجا که آنها صرفاً با یک انتقال عمودی (vertical shift) با هم متفاوتند، شیب در هر مقدار \(x\)، همانند \(x=1\)، برای تمامی این منحنی ها یکسان است. این روش بصری برای اینست که درک کنید چرا هر کدام از این منحنی ها دارای مشتق یکسان می باشند، و بنابراین هر کدام از این منحنی ها ضدمشتقی از تابعی یکسان می باشند.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: