خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
اعداد اول و اعداد مرکب

اعداد اول (Prime numbers) - اعداد کاملی که تنها بر خودشان و بر عدد یک بخش پذیرند - برای قرن ها موضوع بحث بین ریاضیدانان و غیرریاضیدانان بوده اند. اعداد اول و رازهای آنها، فلاسفه، مهندسان، و اخترشناسان را شیفته خود کرده است. این جماعت و سایرین اطلاعات فراوانی را در مورد اعداد اول کشف کرده اند، اما حدس های اثبات نشده زیادی باقی مانده اند. اعداد اول نقش مهمی در رمزگذاری (رمزگذاری کلمات عبور و محافظت از اطلاعات) دارند.

احتمالاً بزرگترین راز اینست که تعیین کنیم، عدد اول بعدی که کشف می شود، چه عددی خواهد بود. کامپیوترها برای جستجو و تشکیل یک لیست جامع از اعداد اول کمک زیادی کرده اند، اما از آنجا که اعداد تا بی نهایت ادامه پیدا می کنند و همینطور از آنجا که هنوز هیچ کس نتوانسته است فرمولی برای پیدا کردن عدد اول بعدی ارائه کند، این سوال که عدد اول بعدی چه می باشد، همواره وجود دارد.
اعداد اول در جبر مهم می باشند زیرا به شما کمک می کنند با کوچکترین عدد ممکن کار کنید. کار با اعداد بزرگ معمولاً خیلی دشوار است و هنگام انجام عملیات ها و حل معادله ها می توانند خطاهای محاسباتی بیشتری را تولید کنند. بنابراین، کاهش کسرها به کوچکترین جملاتشان و فاکتورگیری از عبارتها برای اینکه مسأله بیشتر قابل مدیریت شود وظایف اساسی و مطلوبی هستند.
اولین و کوچکترین عدد اول عدد 2 می باشد. تنها عدد زوج اول نیز همین 2 می باشد. تمامی اعداد اول بعد از 2 فرد می باشند زیرا تمامی اعداد زوج حداقل بر خودشان، بر عدد 1، و بر عدد 2 بخش پذیر می باشند. بنابراین اعداد زوج بزرگتر از 2 در تعریف یک عدد اول نمی گنجند.
در اینجا لیست 46 عدد اول آغازین را می بینید:
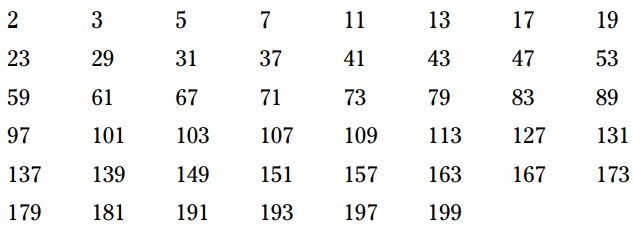
هنگامی که شما قبلاً تشخیص داده باشید که یک عدد، عدد اول می باشد، در هنگام کاهش یک کسر یا فاکتورگیری از یک عبارت، زمان را برای پیدا کردن اعدادی که ممکن است این عدد بر آنها بخش پذیر باشد هدر نمی دهید. اعداد اول بی شماری وجود دارند و عملاً حفظ کردن و حتی شناختن همه آنها ممکن نمی باشد، اما صرفاً دانستن و به حافظه سپردن اعداد اول کوچکتر از 100 یک کمک بزرگ است، و حفظ کردن 46 عدد اول آغازین (تمامی اعداد اول کوچکتر از 200) می تواند یک پاداش باشد.
اعداد اول برای اینکه مورد تفکر واقع شوند چیز جالبی اند، اما به لحاظ فاکتورگیری از عبارتهای جبری یا کاهش کسرها می توانند یک بُن بست باشند. در نقطۀ مقابل اعداد اول، اعداد مرکب قرار دارند که می توانند به تکه های قابل فاکتورگیری و قابل کاهش شکسته شوند. در این بخش، شما طی فرآیندی که فاکتورگیری اول (prime factorization) نام دارد، خواهید دید چگونه هر عدد مرکب حاصلضربی از اعداد اول می باشد. فاکتورگیری اول (prime factorization) هر عددی منحصر به فرد می باشد.
در اینجا چند مثال از فاکتورگیری اول می بینید:
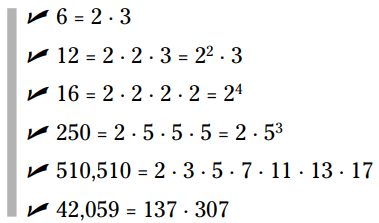
بسیار خوب، آخرین مورد یک چیز خاص و غیرمعمول می باشد. پیدا کردن فاکتورهای اول آن بدون استفاده از ماشین حساب، کامپیوتر، یا یک لیست از اعداد اول بسیار مشکل است.
فاکتورهای برخی اعداد همیشه آشکار نیستند، اما من چند تکنیک دارم که به شما کمک می کند فاکتورهای اول را بنویسید، در ادامه فصل در موردش خواهم گفت.

احتمالاً بزرگترین راز اینست که تعیین کنیم، عدد اول بعدی که کشف می شود، چه عددی خواهد بود. کامپیوترها برای جستجو و تشکیل یک لیست جامع از اعداد اول کمک زیادی کرده اند، اما از آنجا که اعداد تا بی نهایت ادامه پیدا می کنند و همینطور از آنجا که هنوز هیچ کس نتوانسته است فرمولی برای پیدا کردن عدد اول بعدی ارائه کند، این سوال که عدد اول بعدی چه می باشد، همواره وجود دارد.
شروع با مبانی
اعداد اول در جبر مهم می باشند زیرا به شما کمک می کنند با کوچکترین عدد ممکن کار کنید. کار با اعداد بزرگ معمولاً خیلی دشوار است و هنگام انجام عملیات ها و حل معادله ها می توانند خطاهای محاسباتی بیشتری را تولید کنند. بنابراین، کاهش کسرها به کوچکترین جملاتشان و فاکتورگیری از عبارتها برای اینکه مسأله بیشتر قابل مدیریت شود وظایف اساسی و مطلوبی هستند.
قوانین جبر: یک عدد اول (prime number) یک عدد کامل است که بزرگتر از عدد 1 می باشد و فقط بر خودش و 1 بخش پذیر است.
اولین و کوچکترین عدد اول عدد 2 می باشد. تنها عدد زوج اول نیز همین 2 می باشد. تمامی اعداد اول بعد از 2 فرد می باشند زیرا تمامی اعداد زوج حداقل بر خودشان، بر عدد 1، و بر عدد 2 بخش پذیر می باشند. بنابراین اعداد زوج بزرگتر از 2 در تعریف یک عدد اول نمی گنجند.
در اینجا لیست 46 عدد اول آغازین را می بینید:
هنگامی که شما قبلاً تشخیص داده باشید که یک عدد، عدد اول می باشد، در هنگام کاهش یک کسر یا فاکتورگیری از یک عبارت، زمان را برای پیدا کردن اعدادی که ممکن است این عدد بر آنها بخش پذیر باشد هدر نمی دهید. اعداد اول بی شماری وجود دارند و عملاً حفظ کردن و حتی شناختن همه آنها ممکن نمی باشد، اما صرفاً دانستن و به حافظه سپردن اعداد اول کوچکتر از 100 یک کمک بزرگ است، و حفظ کردن 46 عدد اول آغازین (تمامی اعداد اول کوچکتر از 200) می تواند یک پاداش باشد.
اعداد مرکب (Composite Numbers)
اعداد اول برای اینکه مورد تفکر واقع شوند چیز جالبی اند، اما به لحاظ فاکتورگیری از عبارتهای جبری یا کاهش کسرها می توانند یک بُن بست باشند. در نقطۀ مقابل اعداد اول، اعداد مرکب قرار دارند که می توانند به تکه های قابل فاکتورگیری و قابل کاهش شکسته شوند. در این بخش، شما طی فرآیندی که فاکتورگیری اول (prime factorization) نام دارد، خواهید دید چگونه هر عدد مرکب حاصلضربی از اعداد اول می باشد. فاکتورگیری اول (prime factorization) هر عددی منحصر به فرد می باشد.
قوانین جبر: فاکتورگیری اول یک عدد یک حاصلضرب منحصر به فرد از اعداد اول می باشد که نتیجه اش آن عدد خاص می شود. فاکتورگیری اول یک عدد اول، عبارت از فقط خود همان عدد می باشد.
در اینجا چند مثال از فاکتورگیری اول می بینید:
بسیار خوب، آخرین مورد یک چیز خاص و غیرمعمول می باشد. پیدا کردن فاکتورهای اول آن بدون استفاده از ماشین حساب، کامپیوتر، یا یک لیست از اعداد اول بسیار مشکل است.
فاکتورهای برخی اعداد همیشه آشکار نیستند، اما من چند تکنیک دارم که به شما کمک می کند فاکتورهای اول را بنویسید، در ادامه فصل در موردش خواهم گفت.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: