خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
ترسیم نمودار تابع کسینوس

نمودار تابع کسینوس، بسیار شبیه به نمودار تابع سینوس می باشد. این کیفیت به دلیل این واقعیت است که این دو تابع با دامنه و بردشان، و همچنین با چندین اتحاد، به یکدیگر مرتبطند. یک اتحاد که شامل یک انتقال باشد، این ارتباط را بهتر توصیف می کند، زیرا آن انتقال منجر می شود تا نمودار تابع سینوس شبیه به نمودار تابع کسینوس گردد.

ارتباط بین نمودارهای سینوس و کسینوس اینست که کسینوس با سینوسی که \(90\) درجه، یا \(\frac{\pi}{2}\) به سمت چپ منتقل شده باشد، یکسان است. معادله ای که این ارتباط را نشان می دهد برابر با \(\cos x = \sin \biggl(x+\frac{\pi}{2}\biggr)\) می باشد. به نمودارهای توابع سینوس و کسینوس بر روی محورهای مختصات یکسان؛ که در شکل 7-19 نشان داده شده اند، نگاهی بیندازید. هر علامت تیک بر روی محور \(x\) نشان دهندۀ یک واحد می باشد. نمودار کسینوس، منحنی تیره تر است؛ توجه کنید که چگونه به سمت چپ منحنی سینوس، منتقل شده است.
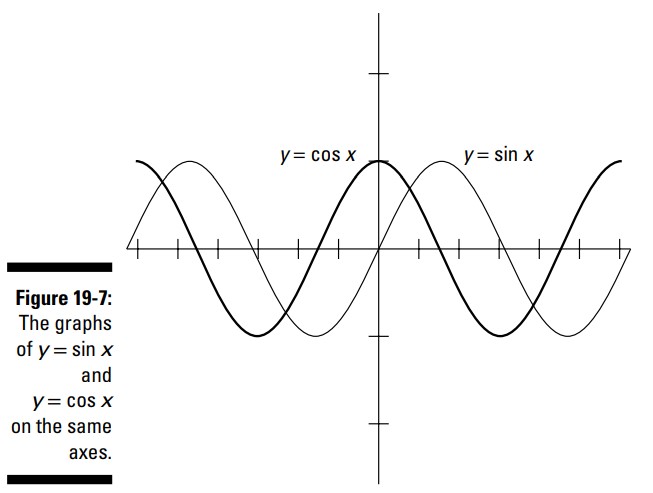
نمودارهای این توابع سینوس و کسینوس یک ویژگی را نشان می دهند که برای چندین جفت از این توابع وجود دارد. این ویژگی مبتنی بر مثلث قائم الزاویه و دو زاویۀ حاده (acute) یا متمم (complementary) در یک مثلث قائم الزاویه می باشد. اتحادهایی که از این مثلث بوجود می آیند اتحادهای توابع مثلثاتی متمم یک زاویه (co-function identities) نامیده می شوند.
این اتحادها نشان می دهند، چگونه مقادیر توابع در زوایای متمم در یک مثلث قائم الزاویه به یکدیگر مرتبطند. به عنوان مثال، \(\cos \theta = \sin (90^{\circ} - \theta)\) بدین معناست که اگر \(\theta\) برابر با \(25\) درجه باشد، سپس \(\cos 25^{\circ}=\sin(90^{\circ}-25^{\circ})=\sin 65^{\circ}\) . این معادله یک روش غیرمستقیم برای تشریح اینست که چرا نمودارهای سینوس و کسینوس صرفاً با اندکی لغزش با یکدیگر متفاوتند. شما احتمالاً متوجه شده اید که این اتحادهای توابع مثلثاتی متمم یک زاویه، همگی از تفاضل بین زوایا استفاده می کنند، اما سُر دادن تابع سینوس به سمت چپ یک جمع است. نمودار سینوس منتقل شده و نمودار کسینوس در واقع معادل یکدیگرند ـــ آنها نمودارهایی از مجموعه نقاطی یکسان هستند.
تابع کسینوس دارای دامنۀ نوسان (amplitude) و دورۀ تناوب (period) یکسانی با تابع سینوس می باشد: دامنۀ نوسان برابر با \(1\)، و دورۀ تناوب برابر با \(2\pi\) یا \(360\) درجه می باشد. دگرگونی های کسینوس مشابه دگرگونی های سینوس عمل می کند. اگر می خواهید دامنۀ نوسان را تغییر دهید، تابع کسینوس را در عددی ضرب می کنید. اگر بخواهید دورۀ تناوب را تغییر دهید، متغیر زاویه را در عددی ضرب یا بر عددی تقسیم می کنید. برای سُر دادن کل منحنی به سمتهای بالا، پایین، راست، یا چپ، عددی را به کل تابع یا متغیر زاویه می افزایید یا از آنها تفریق می کنید.
در معادلۀ \(y=3 \cos x\) ، دامنۀ نوسان برابر با \(3\) می باشد، بدین معنا که این نمودار \(3\) واحد رو به سمت بالا و پایین کِش می آید. نمودار \(y=\cos (x-3)\) معادل \(3\) واحد به سمت راست منتقل می شود. شکل 8-19 این نمودارها را به شما نشان می دهد.
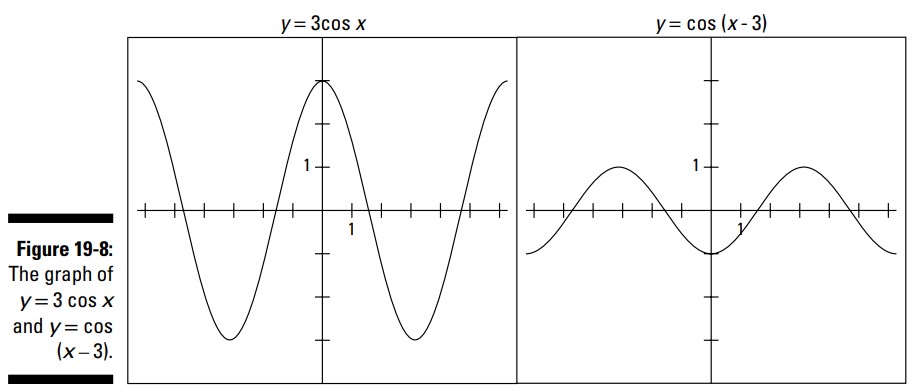
هنگامی که نمودارهای سینوس و کسینوس به اطراف منتقل شده باشند، تفکیک آنها از یکدیگر مشکل می باشد. اما این واقعیت نشان می دهد که این دو تابع چقدر مشترکات دارند، که هنگام به کار گرفتن آنها، به نفع شما تمام می شود.

مقایسۀ سینوس با کسینوس
ارتباط بین نمودارهای سینوس و کسینوس اینست که کسینوس با سینوسی که \(90\) درجه، یا \(\frac{\pi}{2}\) به سمت چپ منتقل شده باشد، یکسان است. معادله ای که این ارتباط را نشان می دهد برابر با \(\cos x = \sin \biggl(x+\frac{\pi}{2}\biggr)\) می باشد. به نمودارهای توابع سینوس و کسینوس بر روی محورهای مختصات یکسان؛ که در شکل 7-19 نشان داده شده اند، نگاهی بیندازید. هر علامت تیک بر روی محور \(x\) نشان دهندۀ یک واحد می باشد. نمودار کسینوس، منحنی تیره تر است؛ توجه کنید که چگونه به سمت چپ منحنی سینوس، منتقل شده است.

نمودارهای این توابع سینوس و کسینوس یک ویژگی را نشان می دهند که برای چندین جفت از این توابع وجود دارد. این ویژگی مبتنی بر مثلث قائم الزاویه و دو زاویۀ حاده (acute) یا متمم (complementary) در یک مثلث قائم الزاویه می باشد. اتحادهایی که از این مثلث بوجود می آیند اتحادهای توابع مثلثاتی متمم یک زاویه (co-function identities) نامیده می شوند.
اتحادهای توابع مثلثاتی متمم یک زاویه (co-function identities) به شرح زیر می باشند:
$$
\begin{array}{c|c}
\sin \theta = \cos (90^{\circ}-\theta) & \csc \theta=\sec(90^{\circ} - \theta) \\
\cos \theta = \sin (90^{\circ} - \theta) & \sec \theta = \csc(90^{\circ} - \theta) \\
\tan \theta=\cot (90^{\circ} - \theta) & \cot \theta = \tan (90^{\circ} - \theta)
\end{array}
$$
$$
\begin{array}{c|c}
\sin \theta = \cos (90^{\circ}-\theta) & \csc \theta=\sec(90^{\circ} - \theta) \\
\cos \theta = \sin (90^{\circ} - \theta) & \sec \theta = \csc(90^{\circ} - \theta) \\
\tan \theta=\cot (90^{\circ} - \theta) & \cot \theta = \tan (90^{\circ} - \theta)
\end{array}
$$
این اتحادها نشان می دهند، چگونه مقادیر توابع در زوایای متمم در یک مثلث قائم الزاویه به یکدیگر مرتبطند. به عنوان مثال، \(\cos \theta = \sin (90^{\circ} - \theta)\) بدین معناست که اگر \(\theta\) برابر با \(25\) درجه باشد، سپس \(\cos 25^{\circ}=\sin(90^{\circ}-25^{\circ})=\sin 65^{\circ}\) . این معادله یک روش غیرمستقیم برای تشریح اینست که چرا نمودارهای سینوس و کسینوس صرفاً با اندکی لغزش با یکدیگر متفاوتند. شما احتمالاً متوجه شده اید که این اتحادهای توابع مثلثاتی متمم یک زاویه، همگی از تفاضل بین زوایا استفاده می کنند، اما سُر دادن تابع سینوس به سمت چپ یک جمع است. نمودار سینوس منتقل شده و نمودار کسینوس در واقع معادل یکدیگرند ـــ آنها نمودارهایی از مجموعه نقاطی یکسان هستند.
استفاده از ویژگی ها برای ترسیم نمودار کسینوس
تابع کسینوس دارای دامنۀ نوسان (amplitude) و دورۀ تناوب (period) یکسانی با تابع سینوس می باشد: دامنۀ نوسان برابر با \(1\)، و دورۀ تناوب برابر با \(2\pi\) یا \(360\) درجه می باشد. دگرگونی های کسینوس مشابه دگرگونی های سینوس عمل می کند. اگر می خواهید دامنۀ نوسان را تغییر دهید، تابع کسینوس را در عددی ضرب می کنید. اگر بخواهید دورۀ تناوب را تغییر دهید، متغیر زاویه را در عددی ضرب یا بر عددی تقسیم می کنید. برای سُر دادن کل منحنی به سمتهای بالا، پایین، راست، یا چپ، عددی را به کل تابع یا متغیر زاویه می افزایید یا از آنها تفریق می کنید.
در معادلۀ \(y=3 \cos x\) ، دامنۀ نوسان برابر با \(3\) می باشد، بدین معنا که این نمودار \(3\) واحد رو به سمت بالا و پایین کِش می آید. نمودار \(y=\cos (x-3)\) معادل \(3\) واحد به سمت راست منتقل می شود. شکل 8-19 این نمودارها را به شما نشان می دهد.

هنگامی که نمودارهای سینوس و کسینوس به اطراف منتقل شده باشند، تفکیک آنها از یکدیگر مشکل می باشد. اما این واقعیت نشان می دهد که این دو تابع چقدر مشترکات دارند، که هنگام به کار گرفتن آنها، به نفع شما تمام می شود.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: