خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
ترسیم نمودار تابع تانژانت

توابع تانژانت و کتانژانت دارای مشابهت های بسیاری می باشند. شما می توانید هر دوی این توابع را به لحاظ سینوس و کسینوس بنویسید، بنابراین آنها مقادیر توابع یکسانی را در نسبتهایشان به اشتراک می گذارند. یک تفاوت بین تانژانت و کتانژانت اینست که آنها در مکانهای یکسانی مقادیر تابع را برای مقادیر \(x\) در دامنۀ شان ندارند ـــ به اندازۀ \(90\) درجه جابجا می شوند. با وجود اینکه دامنه های آنها (یا مقادیر \(x\) شان) محدود شده است، تانژانت و کتانژانت تنها توابع مثلثاتی می باشند که بُردهای آنها (یا مقادیر \(y\) شان) شامل تمامی اعداد از منفی بی نهایت تا مثبت بی نهایت می گردد. همانطور که در این فصل خواهید دید، چالش اصلی در ترسیم نمودار تانژانت و کتانژانت کنار آمدن با محدودیت های دامنه و خطوط مجانب (asymptotes) می باشد، خطوط مجانب، خطهای نقطه دار عمودی هستند که برای تعیین شکل منحنی، مورد استفاده قرار می گیرند.

تابع تانژانت می تواند به شکل نسبتی از سینوس تقسیم بر کسینوس نوشته شود: \(\tan \theta=\frac{\sin \theta}{\cos \theta}\) . (برای اطلاعات بیشتر در مورد تابع تانژانت می توانید فصل های\(7\) و \(8\) را ببینید.) توابع سینوس و کسینوس به ازاء هر مقدار \(x\)، دارای مقادیر معادلی می باشند، بنابراین مهم نیست که چه عددی را در \(x\) قرار می دهید، شما همواره پاسخی را دریافت خواهید کرد. تنها مشکل زمانی رخ می دهد که تابع کسینوس برابر با \(0\) باشد، زیرا یک کسر نمی تواند دارای \(0\) در مخرجش باشد. بنابراین، هرجا که تابع کسینوس برابر با \(0\) باشد، نمودار منحنی تانژانت وجود نخواهد داشت، و این با خطهای مجانب نشان داده می شود. ویژگی جالب دیگر که در اینجا نقشی ایفا می کند این حقیقت است که سینوس و کسینوس هر دو در ربع صفحۀ اول مثبت می باشند و در ربع صفحۀ سوم منفی می باشند. در نتیجه، تانژانت در آن دو ربع صفحه مثبت خواهد بود و در دو ربع صفحۀ دیگر منفی خواهد بود، زیرا یکی از مقادیر سینوس یا کسینوس در آن دو ربع صفحۀ دیگر منفی است.
توابع سینوس و کسینوس دارای دورۀ تناوب \(2\pi\) یا \(360\) درجه می باشند، که بدین معناست که بعد از هر \(2\pi\)، الگوی تابع از نو آغاز می شود. با این حال، در مورد تابع تانژانت، طول این دورۀ تناوب تنها \(\pi\) می باشد ـــ نصف طول سینوس یا کسینوس. تابع تانژانت الگویش را دو برابر بیشتر از سینوس و کسینوس تکرار می کند.
یک خط مجانب (asymptote) خطی است که در جهت دادن به یک نمودار کمک می کند. این خط بخشی از نمودار آن تابع نمی باشد؛ در عوض، با بسیار نزدیک شدن به آن منحنی، به تعیین شکل آن منحنی کمک می کند. خط های مجانب معمولاً به صورت خط های نقطه چین نشان داده می شوند. اگرچه، در صورتیکه از ماشین حساب نموداریتان برای ترسیم منحنی یک تانژانت استفاده کنید، خطهای مجانب به شکل خطهای توپر نشان داده می شوند. ظاهراً ماشین حساب تمایل دارد همه چیز را متصل نگهدارد. فقط یادتان باشد که این خط مجانب صرفاً برای شکل دهی آنجاست.
خطهای مجانب برای نمودار تابع تانژانت مرتباً رخ می دهند، هر کدام از آنها \(\pi\) یا \(180\) درجه با یکدیگر فاصله دارند. آنها هر بخش از منحنی تانژانت را تفکیک می کنند، یا هر چرخۀ کامل را از بعدی جدا می کنند.
معادلات خطهای مجانب تانژانت همگی در شکل \(y=\frac{\pi}{2}(2\pi+1)\) می باشند، که در آن \(n\) عددی صحیح است. تحت قراردادی برای \(n\)، عبارت \(2n+1\) همواره نتیجه اش عددی فرد خواهد بود. با جایگزین کردن \(n\) با اعداد صحیح، خطهایی همچون اینها را بدست خواهید آورد:
$$y=\frac{\pi}{2},y=\frac{3\pi}{2},y=\frac{7\pi}{2},y=-\frac{\pi}{2},y=-\frac{3\pi}{2},y=-\frac{5\pi}{2},y=-\frac{7\pi}{2}$$
دلیل اینکه این خطهای مجانب همیشه در این مضربهای فرد از \(\frac{\pi}{2}\) رخ می دهند، اینست که این نقاط محل هایی هستند که در آنها تابع کسینوس برابر با \(0\) می باشد. به این ترتیب، دامنۀ تابع تانژنت شامل تمام اعداد حقیقی به استثناء اعدادی که در این خطهای مجانب رخ می دهند، می باشد.
شکل 1-20 ظاهر نمودار تانژانت را نشان می دهد. مقادیر تانژانت با نزدیک شدن اندازۀ زاویه ها به \(90\) درجه، \(270\) درجه، و به همین ترتیب بی نهایت بالا می روند (همینطور که از سمت چپ به راست این نمودار پیش می روید). با نزدیک شدن اندازۀ زوایا به \(-90\) درجه، \(-270\) درجه و به همین ترتیب، این مقادیر بی نهایت پایین می روند (همینطور که از سمت راست به چپ این نمودار پیش می روید).
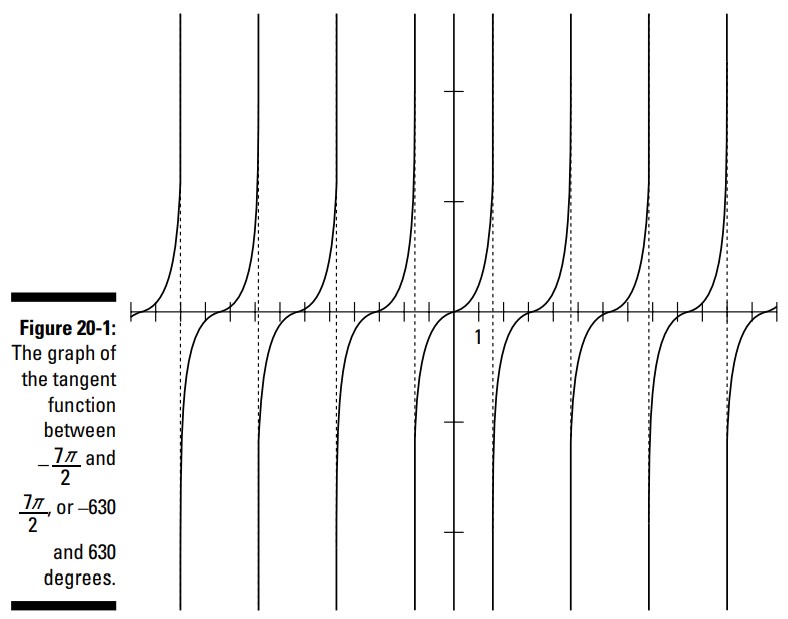
همانطور که می بینید، تابع تانژانت مقادیرش را بارها و بارها تکرار می کند. یک تفاوت عمده بین این تابع و توابع سینوس و کسینوس در اینست که دارای اینهمه وقفه (شکاف) بین چرخه هایش می باشد. همینطور که از چپ به راست پیش می روید، تانژانت طوری ظاهر می شود که به سمت مثبت بی نهایت پیش می رود. در واقع در بالای نمودار مخفی می گردد و سپس از پایین سر بر می آورد، جایی که مقادیر آن از منفی بی نهایت می آیند. ماشین حسابهای نموداری، و سایر ابزارهای ترسیم نمودار معمولاً مخفی شدن نمودار در بالای صفحه را نشان نمی دهند، بنابراین به شما بستگی دارد که بدانید در واقعیت چه چیزی رخ می دهد، حتی اگر تصویر دقیقاً آن گونه به نظر نرسد.
شما می توانید تابع تانژانت را با ضرب کردن، جمع کردن، و تفریق کردن، ویرایش کنید. در برخی موارد، تاثیرات این تغییرات مشابه آنهایی هستند که در هنگام ویرایش توابع سینوس و کسینوس رخ می دهند. از آنجا که این نتایج همیشه یکسان نیستند، شما باید این تغییرات را به صورت اساسی مورد به مورد در نظر بگیرید.
شما می توانید تابع تانژانت را در عددی ضرب کنید، اما انجام این کار همان تاثیری را که ضرب کردن در تابع سینوس می گذارد، نخواهد داشت. ضرب کردن تابع سینوس در یک عدد، دامنۀ نوسان آن را تغییر می دهد، و منجر می شود تا آن تابع شامل مقادیر بزرگتر و کوچکتر گردد. با این حال، مقادیر تانژانت، در حال حاضر از منفی بی نهایت تا مثبت بی نهایت پیش می روند.
هنگامی که کل تابع تانژانت را در عددی ضرب می کنید، آنچه که اتفاق می افتد این موارد است:
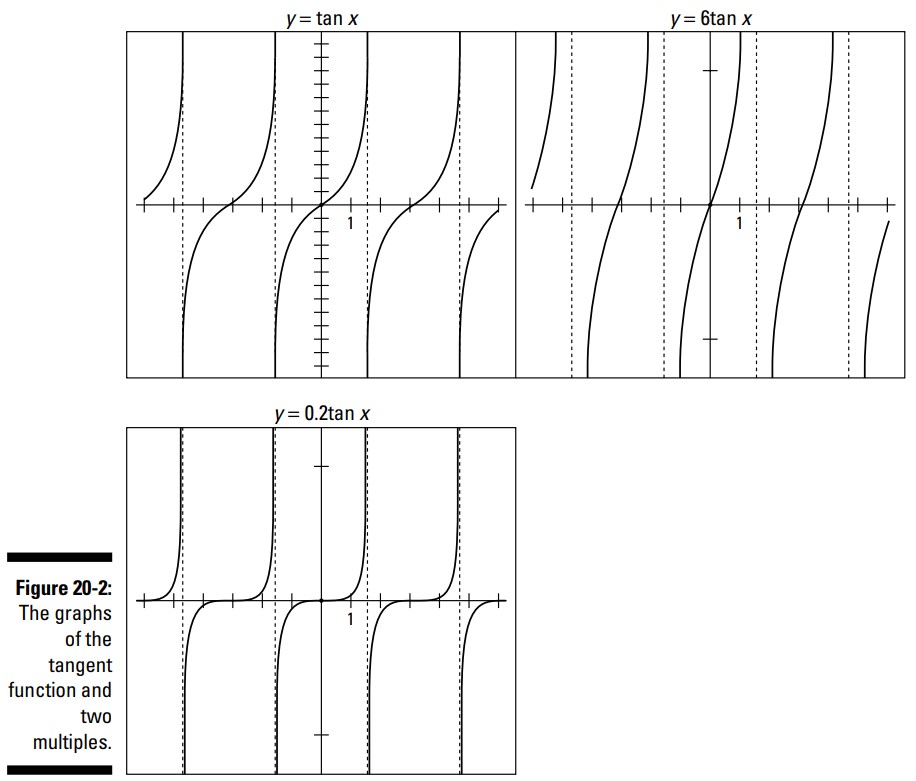
شکل 2-20 نمودار تابع اصلی تانژانت (\(y=\tan x\)) و دو مضرب از آن را برای توصیف این ویژگی، نشان می دهد. توجه کنید که چگونه مضربی از \(6\) منحنی تانژانت را تندتر می کند، در حالیکه مضربی از \(0.2\) آن را مسطح تر می کند. هر دوی این توابع هنوز هم دارای مقادیری هستند که از منفی بی نهایت تا مثبت بی نهایت می روند، اما نرخی که با آن به آنجا می روند تغییر می کند.
ضرب کردن در متغیر زاویه در تابع تانژانت همان تاثیری را دارد که در توابع سینوس و کسینوس دارد. اگر این مضرب برابر با \(2\) باشد، مانند \(y=\tan 2x\)، آن گاه تابع تانژانت در همان فضای معمول، دوبرابر چرخه ایجاد می کند. به عبارت دیگر، دورۀ تناوب برابر با \(\frac{\pi}{2}\) می باشد، که برابر با دورۀ تناوب معمول تانژانت یعنی \(\pi\)، تقسیم بر \(2\) می باشد. از آنجا که ضرب کردن در متغیر زاویه در تابع تانژانت، نتیجه اش کاملاً مشابه نتیجۀ حاصله در توابع سینوس و کسینوس می باشد، در اینجا وارد جزئیاتش نمی شوم ـــ برای اطلاعات بیشتر در این زمینه به فصل 19 مراجعه کنید.
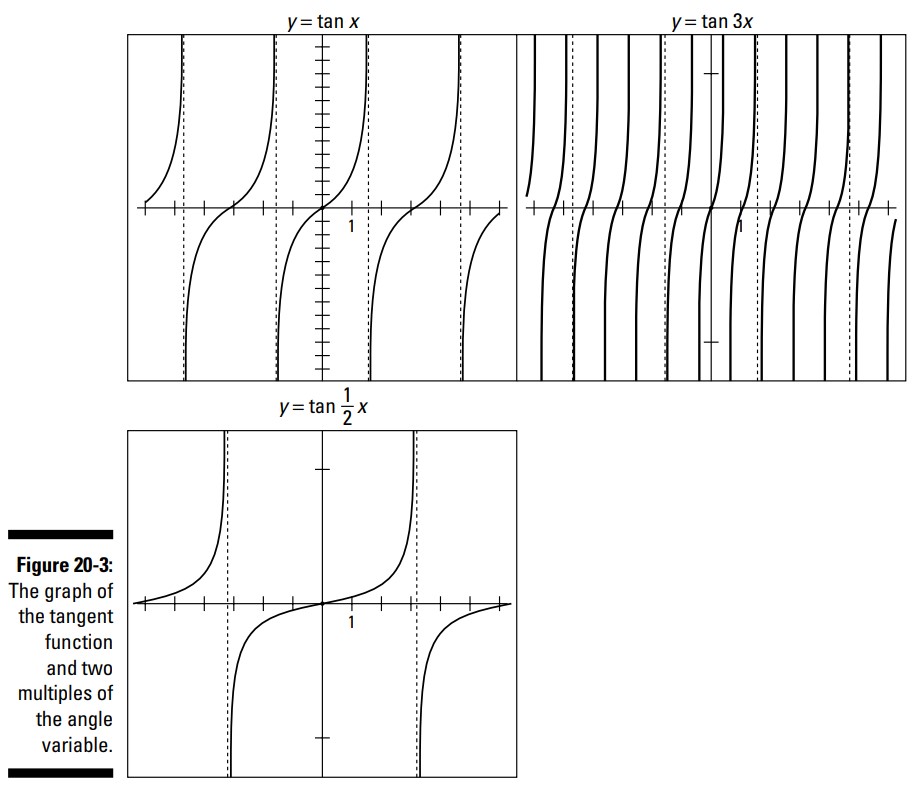
شکل 3-20 چندین نمودار را نشان می دهد که تاثیر ضرب کردن متغیر زاویه در عددی بزرگتر از \(1\) و سپس در عددی بین \(0\) و \(1\) نشان می دهد.
نمودار \(y=\tan 3x\) تمامی خطهای مجانب را نشان نمی دهد، اما سه برابر حد معمول، منحنی های تانژانت را در خودش جای داده است. نمودار \(y=\tan \frac{1}{2}x\) صرفاً دارای نیمی از این چرخه ها است ـــ یا دوبرابر حد معمول طول می کشد تا یک چرخه را تکمیل کند.
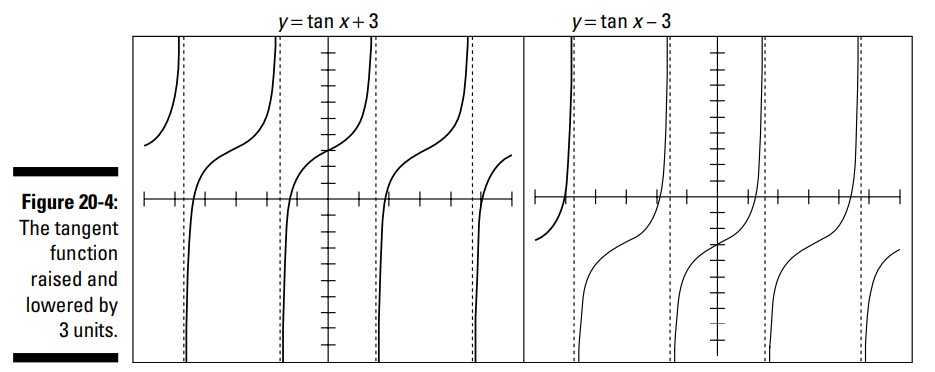
افزودن یک عدد به تابع تانژانت منجر به بالا رفتن منحنی روی نمودار به همان میزان می شود. به همین ترتیب، تفریق یک عدد، این منحنی را پایین می آورد. از آنجا که تابع تانژانت دارای مقادیری از منفی بی نهایت تا مثبت بی نهایت می باشد، افزودن به تابع یا تفریق از تابع، مقادیری را که آن تابع دارد، تغییر نمی دهد ـــ فقط محل قرارگیری آنها را تغییر می دهد. هنگامی که مقداری را به تابع تانژانت می افزایید یا از آن تفریق می کنید، نقطۀ تغییر تحدب منحنی تانژانت (point of inflection) به سمت بالا یا پایین منتقل می شود ـــ نقطۀ تغییر تحدب منحنی تانژانت جایی است که منحنی اندکی مسطح به نظر می آید. شکل 4-20 چندین نمودار را برای توصیف این انتقال، نشان می دهد.
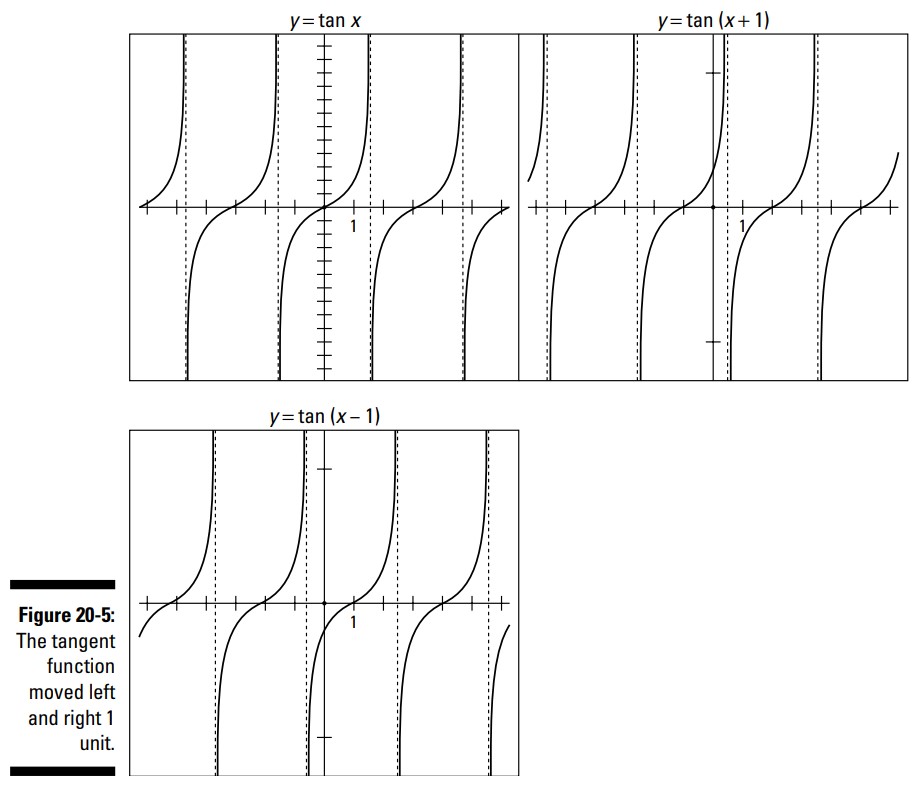
افزودن یا تفریق عددی به یا از متغیر زاویه در تابع تانژانت همان تاثیری را دارد که این کار در توابع سینوس و کسینوس دارد ـــ منحنی را به سمت راست یا چپ منتقل می کند. نمودار \(y=\tan(x+1)\) همراه با خطهای مجانبش، یک واحد به سمت چپ منتقل می شود. نمودار \(y=\tan(x-1)\) همه چیز را یک واحد به سمت راست منتقل می کند. شکل 5-20 مقایسه ای بین تابع تانژانت و این دو منحنی منتقل شده را انجام می دهد.

بررسی تانژانت
تابع تانژانت می تواند به شکل نسبتی از سینوس تقسیم بر کسینوس نوشته شود: \(\tan \theta=\frac{\sin \theta}{\cos \theta}\) . (برای اطلاعات بیشتر در مورد تابع تانژانت می توانید فصل های\(7\) و \(8\) را ببینید.) توابع سینوس و کسینوس به ازاء هر مقدار \(x\)، دارای مقادیر معادلی می باشند، بنابراین مهم نیست که چه عددی را در \(x\) قرار می دهید، شما همواره پاسخی را دریافت خواهید کرد. تنها مشکل زمانی رخ می دهد که تابع کسینوس برابر با \(0\) باشد، زیرا یک کسر نمی تواند دارای \(0\) در مخرجش باشد. بنابراین، هرجا که تابع کسینوس برابر با \(0\) باشد، نمودار منحنی تانژانت وجود نخواهد داشت، و این با خطهای مجانب نشان داده می شود. ویژگی جالب دیگر که در اینجا نقشی ایفا می کند این حقیقت است که سینوس و کسینوس هر دو در ربع صفحۀ اول مثبت می باشند و در ربع صفحۀ سوم منفی می باشند. در نتیجه، تانژانت در آن دو ربع صفحه مثبت خواهد بود و در دو ربع صفحۀ دیگر منفی خواهد بود، زیرا یکی از مقادیر سینوس یا کسینوس در آن دو ربع صفحۀ دیگر منفی است.
تعیین دورۀ تناوب
توابع سینوس و کسینوس دارای دورۀ تناوب \(2\pi\) یا \(360\) درجه می باشند، که بدین معناست که بعد از هر \(2\pi\)، الگوی تابع از نو آغاز می شود. با این حال، در مورد تابع تانژانت، طول این دورۀ تناوب تنها \(\pi\) می باشد ـــ نصف طول سینوس یا کسینوس. تابع تانژانت الگویش را دو برابر بیشتر از سینوس و کسینوس تکرار می کند.
تعیین خطوط مجانب
یک خط مجانب (asymptote) خطی است که در جهت دادن به یک نمودار کمک می کند. این خط بخشی از نمودار آن تابع نمی باشد؛ در عوض، با بسیار نزدیک شدن به آن منحنی، به تعیین شکل آن منحنی کمک می کند. خط های مجانب معمولاً به صورت خط های نقطه چین نشان داده می شوند. اگرچه، در صورتیکه از ماشین حساب نموداریتان برای ترسیم منحنی یک تانژانت استفاده کنید، خطهای مجانب به شکل خطهای توپر نشان داده می شوند. ظاهراً ماشین حساب تمایل دارد همه چیز را متصل نگهدارد. فقط یادتان باشد که این خط مجانب صرفاً برای شکل دهی آنجاست.
خطهای مجانب برای نمودار تابع تانژانت مرتباً رخ می دهند، هر کدام از آنها \(\pi\) یا \(180\) درجه با یکدیگر فاصله دارند. آنها هر بخش از منحنی تانژانت را تفکیک می کنند، یا هر چرخۀ کامل را از بعدی جدا می کنند.
معادلات خطهای مجانب تانژانت همگی در شکل \(y=\frac{\pi}{2}(2\pi+1)\) می باشند، که در آن \(n\) عددی صحیح است. تحت قراردادی برای \(n\)، عبارت \(2n+1\) همواره نتیجه اش عددی فرد خواهد بود. با جایگزین کردن \(n\) با اعداد صحیح، خطهایی همچون اینها را بدست خواهید آورد:
$$y=\frac{\pi}{2},y=\frac{3\pi}{2},y=\frac{7\pi}{2},y=-\frac{\pi}{2},y=-\frac{3\pi}{2},y=-\frac{5\pi}{2},y=-\frac{7\pi}{2}$$
دلیل اینکه این خطهای مجانب همیشه در این مضربهای فرد از \(\frac{\pi}{2}\) رخ می دهند، اینست که این نقاط محل هایی هستند که در آنها تابع کسینوس برابر با \(0\) می باشد. به این ترتیب، دامنۀ تابع تانژنت شامل تمام اعداد حقیقی به استثناء اعدادی که در این خطهای مجانب رخ می دهند، می باشد.
شکل 1-20 ظاهر نمودار تانژانت را نشان می دهد. مقادیر تانژانت با نزدیک شدن اندازۀ زاویه ها به \(90\) درجه، \(270\) درجه، و به همین ترتیب بی نهایت بالا می روند (همینطور که از سمت چپ به راست این نمودار پیش می روید). با نزدیک شدن اندازۀ زوایا به \(-90\) درجه، \(-270\) درجه و به همین ترتیب، این مقادیر بی نهایت پایین می روند (همینطور که از سمت راست به چپ این نمودار پیش می روید).

همانطور که می بینید، تابع تانژانت مقادیرش را بارها و بارها تکرار می کند. یک تفاوت عمده بین این تابع و توابع سینوس و کسینوس در اینست که دارای اینهمه وقفه (شکاف) بین چرخه هایش می باشد. همینطور که از چپ به راست پیش می روید، تانژانت طوری ظاهر می شود که به سمت مثبت بی نهایت پیش می رود. در واقع در بالای نمودار مخفی می گردد و سپس از پایین سر بر می آورد، جایی که مقادیر آن از منفی بی نهایت می آیند. ماشین حسابهای نموداری، و سایر ابزارهای ترسیم نمودار معمولاً مخفی شدن نمودار در بالای صفحه را نشان نمی دهند، بنابراین به شما بستگی دارد که بدانید در واقعیت چه چیزی رخ می دهد، حتی اگر تصویر دقیقاً آن گونه به نظر نرسد.
از آنجا که ماشین حسابهای نموداری سعی می کنند تا تابع تانژانت را متصل کنند تا آن را بر روی صفحه پیوسته سازند، شما در درک صحیح واقعیت با خطا مواجه می شوید. تنها روش رها شدن از این خطهای اضافی اینست که ماشین حسابتان را به حالت dot (نقطه) تنظیم کنید که حالت مقابل connected (متصل) می باشد. بیشتر ماشین حسابها روشهایی برای تنظیم حالت برای چیزهایی همچون رادیان و درجه، نمودارهای نقطه چین و نمودارهای متصل، اعداد اعشاری با تعداد ارقام اعشار شناور و با تعداد ارقام اعشار ثابت، و ... دارند. انجام دادن این تغییرات معمولاً ساده است، کافیست راهنمای ماشین حسابتان را بررسی کنید. بخش سختش اینست که یادتان بماند در چه حالتی قرار دارید.
ویرایش تابع تانژانت
شما می توانید تابع تانژانت را با ضرب کردن، جمع کردن، و تفریق کردن، ویرایش کنید. در برخی موارد، تاثیرات این تغییرات مشابه آنهایی هستند که در هنگام ویرایش توابع سینوس و کسینوس رخ می دهند. از آنجا که این نتایج همیشه یکسان نیستند، شما باید این تغییرات را به صورت اساسی مورد به مورد در نظر بگیرید.
ضرب کردن در تابع تانژانت
شما می توانید تابع تانژانت را در عددی ضرب کنید، اما انجام این کار همان تاثیری را که ضرب کردن در تابع سینوس می گذارد، نخواهد داشت. ضرب کردن تابع سینوس در یک عدد، دامنۀ نوسان آن را تغییر می دهد، و منجر می شود تا آن تابع شامل مقادیر بزرگتر و کوچکتر گردد. با این حال، مقادیر تانژانت، در حال حاضر از منفی بی نهایت تا مثبت بی نهایت پیش می روند.
هنگامی که کل تابع تانژانت را در عددی ضرب می کنید، آنچه که اتفاق می افتد این موارد است:
-
اگر آن را در عددی بزرگتر از \(1\) ضرب کنید، نمودار آن تابع خیلی سریعتر تُند می شود.
-
اگر آن را در کسری بین \(0\) و \(1\) ضرب کنید، نمودار آن تابع مسطح تر می شود.
-
اگر آن را در عددی منفی ضرب کنید، بر روی محور \(x\) می چرخد. برای اطلاعات بیشتر در مورد این چرخش ها (که بازتاب ها نامیده می شوند)، فصل 3 را ببینید.
شکل 2-20 نمودار تابع اصلی تانژانت (\(y=\tan x\)) و دو مضرب از آن را برای توصیف این ویژگی، نشان می دهد. توجه کنید که چگونه مضربی از \(6\) منحنی تانژانت را تندتر می کند، در حالیکه مضربی از \(0.2\) آن را مسطح تر می کند. هر دوی این توابع هنوز هم دارای مقادیری هستند که از منفی بی نهایت تا مثبت بی نهایت می روند، اما نرخی که با آن به آنجا می روند تغییر می کند.

ضرب کردن در متغیر زاویه در تابع تانژانت
ضرب کردن در متغیر زاویه در تابع تانژانت همان تاثیری را دارد که در توابع سینوس و کسینوس دارد. اگر این مضرب برابر با \(2\) باشد، مانند \(y=\tan 2x\)، آن گاه تابع تانژانت در همان فضای معمول، دوبرابر چرخه ایجاد می کند. به عبارت دیگر، دورۀ تناوب برابر با \(\frac{\pi}{2}\) می باشد، که برابر با دورۀ تناوب معمول تانژانت یعنی \(\pi\)، تقسیم بر \(2\) می باشد. از آنجا که ضرب کردن در متغیر زاویه در تابع تانژانت، نتیجه اش کاملاً مشابه نتیجۀ حاصله در توابع سینوس و کسینوس می باشد، در اینجا وارد جزئیاتش نمی شوم ـــ برای اطلاعات بیشتر در این زمینه به فصل 19 مراجعه کنید.
شکل 3-20 چندین نمودار را نشان می دهد که تاثیر ضرب کردن متغیر زاویه در عددی بزرگتر از \(1\) و سپس در عددی بین \(0\) و \(1\) نشان می دهد.
نمودار \(y=\tan 3x\) تمامی خطهای مجانب را نشان نمی دهد، اما سه برابر حد معمول، منحنی های تانژانت را در خودش جای داده است. نمودار \(y=\tan \frac{1}{2}x\) صرفاً دارای نیمی از این چرخه ها است ـــ یا دوبرابر حد معمول طول می کشد تا یک چرخه را تکمیل کند.

افزودن عددی به تابع تانژانت
افزودن یک عدد به تابع تانژانت منجر به بالا رفتن منحنی روی نمودار به همان میزان می شود. به همین ترتیب، تفریق یک عدد، این منحنی را پایین می آورد. از آنجا که تابع تانژانت دارای مقادیری از منفی بی نهایت تا مثبت بی نهایت می باشد، افزودن به تابع یا تفریق از تابع، مقادیری را که آن تابع دارد، تغییر نمی دهد ـــ فقط محل قرارگیری آنها را تغییر می دهد. هنگامی که مقداری را به تابع تانژانت می افزایید یا از آن تفریق می کنید، نقطۀ تغییر تحدب منحنی تانژانت (point of inflection) به سمت بالا یا پایین منتقل می شود ـــ نقطۀ تغییر تحدب منحنی تانژانت جایی است که منحنی اندکی مسطح به نظر می آید. شکل 4-20 چندین نمودار را برای توصیف این انتقال، نشان می دهد.

افزودن یا تفریق عددی به یا از متغیر زاویه در تابع تانژانت همان تاثیری را دارد که این کار در توابع سینوس و کسینوس دارد ـــ منحنی را به سمت راست یا چپ منتقل می کند. نمودار \(y=\tan(x+1)\) همراه با خطهای مجانبش، یک واحد به سمت چپ منتقل می شود. نمودار \(y=\tan(x-1)\) همه چیز را یک واحد به سمت راست منتقل می کند. شکل 5-20 مقایسه ای بین تابع تانژانت و این دو منحنی منتقل شده را انجام می دهد.

اگر برای تفکیک این نمودارها، کار سختی پیش رو دارید، کافیست به نقطۀ تغییر تحدب منحنی آنها نگاهی بیندازید. این نقطه یک علامت مرجع خوب برای مواقعی است که این تغییرات را بررسی می کنید.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: