خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
تمرین 17: نامساوی های درجه دوم با یک متغیر، توسعه

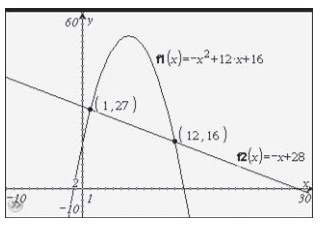
نمودار زیر پاسخ نامساوی \(-x^2 + 12x + 16 \ge -x + 28\) را نشان می دهد.



-
چرا \(1 \le x \le 12\) پاسخ این نامساوی می باشد؟
-
این نامساوی را طوری بازچینش کنید که به شکل \(q(x) \ge 0\) در آید، در این نامساوی \(q(x)\) یک عبارت درجه دوم می باشد.
-
نامساوی تعیین شده در بخش b را حل کنید.
-
ارتباط بین پاسخ های بخش a و c چه می باشند؟ توضیح دهید.
پاسخ
-
دلیل این که \(1 \le x \le 12\) پاسخ این نامساوی می باشد، اینست که در این بازۀ مقادیر \(x\) ها، نمودار سهمی در بالای نمودار خط قرار دارد و طبیعتاً از آن بزرگتر است یا مساوی با آن است.
-
$$
-x^2 + 13x - 12 \ge 0
$$
همچنین اگر دو طرف این نامساوی را در \(-1\) ضرب کنیم، خواهیم داشت:
$$
x^2 -13x +12 \le 0
$$
-
برای حل این نامساوی ابتدا آن را فاکتورگیری می کنیم، سپس ریشه های آن را بدست می آوریم و بر روی خط اعداد با روش بررسی موردی می سنجیم که پاسخ هر بازه مثبت یا منفی می باشد.
$$
x^2 - 13x + 12 \le 0\\
(x-12)(x-1) \le 0
$$
پاسخ این نامساوی \(1 \le x \le 12\) می باشد.
-
پاسخ های بخش a و c یکسان می باشند. منطقی هم می باشد که هر دو پاسخ یکسان باشند، زیرا در واقع این دو نامساوی یک چیز می باشند.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: