خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
تمرین 8: نامساوی های درجه دوم با یک متغیر، تمرین

نامساوی های زیر را حل کنید. راهبرد تان برای حل مسئله و همچنین دلیل استفاده از آن راهبرد خاص را توضیح دهید.

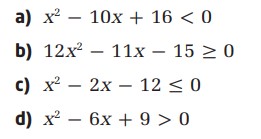
نکته: راهبردهای مورد استفادۀ شما برای حل این تمرین ممکن است متفاوت باشند و هیچ اشکالی هم ندارد. در واقع بهترین راهبرد چیزی است که شما با آن راحت تر باشید. از این رو راهبردی که ما برای حل هر مورد استفاده کرده ایم، یک ترجیح شخصی است و الزاماً بهترین راهبرد ممکن نمی باشد.

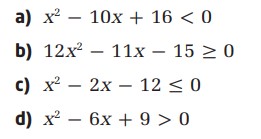
پاسخ
نکته: راهبردهای مورد استفادۀ شما برای حل این تمرین ممکن است متفاوت باشند و هیچ اشکالی هم ندارد. در واقع بهترین راهبرد چیزی است که شما با آن راحت تر باشید. از این رو راهبردی که ما برای حل هر مورد استفاده کرده ایم، یک ترجیح شخصی است و الزاماً بهترین راهبرد ممکن نمی باشد.
-
در این مورد از ترسیم نمودار برای حل مسئله استفاده می کنیم. زیرا ترسیم نمودار این نامساوی ساده است. البته به دلیل اینکه این نامساوی را به سادگی می توان فاکتورگیری کرد و به شکل \((x-8)(x-2) \lt 0\) بازنویسی کرد، راهبرد تجزیه و تحلیل موردی نیز به سادگی قابل اِعمال می باشد.
$$
\{ x | 2 \lt x \lt 8 , x \in R \}
$$
-
با توجه به ساده بودن فاکتورگیری، از تجزیه و تحلیل علامت ها استفاده می کنیم.
$$
\{ x | x \le -\frac{3}{4} \text{ or } x \ge \frac{5}{3}, x \in R \}
$$
-
با توجه به سخت بودن فاکتورگیری و نیاز به فرمول حل معادلۀ درجه دوم، از روش ترسیم نمودار به کمک فناوری استفاده می کنیم.
$$
\{ x | 1 - \sqrt{13} \le x \le 1 + \sqrt{13} , x \in R \}
$$
-
از آنجا که فاکتورگیری این نامساوی ساده است، از تجزیه و تحلیل موردی استفاده می کنیم.
$$
\{ x | x \ne 3 , x \in R \}
$$
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: