خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
تست خط عمودی در توابع

تمامی منحنی های موجود در صفحۀ مختصات را نمی توان نمودار یک تابع به حساب آورد. تابع \(f\) به ازاء هر مقدار \(x\) که در دامنۀ آن باشد، می تواند فقط یک مقدار \(f(x)\) داشته باشد. بنابراین هیچ خط عمودی نمی تواند نمودار یک تابع را بیش از یک بار قطع کند. اگر \(a\) در دامنۀ تابع \(f\) باشد، آن گاه خط عمودیِ \(x=a\) نمودار \(f\) را تنها در یک نقطه، \((a , f(a))\)، قطع خواهد کرد.

دایره نمی تواند نمودار یک تابع باشد، زیرا برخی از خطوط عمودی می توانند دایره را در بیش از یک نقطه قطع کنند. در شکل زیر تصویر a نمودار یک تابع نیست، اما دو نیم دایره موجود در تصاویر b و c نمودار یک تابع می باشند. از آزمایش خط عمودی می توان برای تعیین اینکه یک نمودار مرتبط به یک تابع می باشد یا نه استفاده کرد.
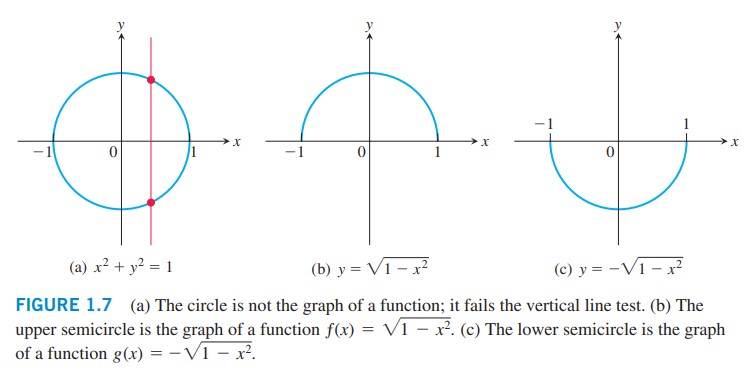

دایره نمی تواند نمودار یک تابع باشد، زیرا برخی از خطوط عمودی می توانند دایره را در بیش از یک نقطه قطع کنند. در شکل زیر تصویر a نمودار یک تابع نیست، اما دو نیم دایره موجود در تصاویر b و c نمودار یک تابع می باشند. از آزمایش خط عمودی می توان برای تعیین اینکه یک نمودار مرتبط به یک تابع می باشد یا نه استفاده کرد.

ترجمۀ شکل:
شکل \(\text{1.7}\):
شکل \(\text{1.7}\):
-
این دایره نمودار یک تابع نمی باشد؛ زیرا نمی تواند آزمون خط عمودی را پاس کند.
-
نیم دایرۀ بالای محور \(x\)، نمودار تابع \(f(x) = \sqrt{1-x^2}\) می باشد.
-
نیم دایرۀ پایین محور \(x\)، نمودار تابع \(g(x) = -\sqrt{1-x^2}\) می باشد.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: