پاسخنامه کسرها

نویسنده : امیر انصاری

در اینجا پاسخ تمریناتی را داریم که به موضوع کسرها می پردازند. برای مشاهدۀ خود سوالات اینجا کلیک کنید.

1. \(\frac{1}{3}\)
2. \(\frac{3}{4}\)
3. \(\frac{5}{6}\)
4. \(\frac{7}{12}\)
1. صورت کسر یعنی عدد \(3\) بزرگتر از مخرج کسر یعنی \(2\) است، پس \(\frac{3}{2}\) یک کسر ناسره (improper fraction) می باشد.
2. صورت کسر، عدد \(8\) بزرگتر از مخرج \(9\) است، پس \(\frac{8}{9}\) یک کسر سره (proper fraction) می باشد.
3. صورت کسر یعنی \(20\) کوچکتر از مخرج آن یعنی \(23\) است، پس \(\frac{20}{23}\) یک کسر سره است.
4. صورت کسر، \(75\)، بزرگتر از مخرج آن، \(51\)، است، پس \(\frac{75}{51}\) یک کسر ناسره است.
1. \(\frac{3}{3}=1\)
2. \(\frac{10}{1}=10\)
3. \(\frac{10}{10}=1\)
4. \(\frac{81}{1}=81\)
1. کسرمتقابل \(\frac{5}{7}\) برابر با \(\frac{7}{5}\) می باشد.
2. کسر متقابل \(\frac{10}{3}\) برابر با \(\frac{3}{10}\) می باشد.
3. کسر متقابل \(\frac{12}{17}\) برابر با \(\frac{17}{12}\) می باشد.
4. کسر متقابل \(\frac{80}{91}\) برابر با \(\frac {91}{80}\) می باشد.
\(5\frac{1}{4}=\frac{(5 \cdot 4+1)}{4}=\frac{21}{4}\)
\(7\frac{2}{9}=\frac{(7 \cdot 9+2)}{9}=\frac{65}{9}\)
\(10\frac{5}{12}=\frac{(10 \cdot 12+5)}{12}=\frac{125}{12}\)
\(\frac{13}{4}=3\frac{1}{4}\)
صورت کسر، \(13\)، را بر مخرج آن، \(4\)، تقسیم کنید:

پاسختان را به این شکل بسازید که خارج قسمت (quotient) یعنی \(3\) را به عنوان عدد صحیح و باقیمانده (remainder) یعنی \(1\) را بعنوان صورت کسر بنویسید، مخرج به همان شکل اول باقی می ماند: \(3\frac{1}{4}\)
\(\frac{29}{10}=2\frac{9}{10}\)
\(\frac{100}{7}=14\frac{2}{7}\)
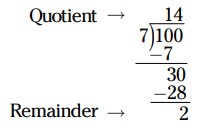
\(\frac{2}{3}=\frac{12}{18}\)
برای حل این مسأله ابتدا آن را به شکل زیر بنویسید:
\(\frac{2}{3}=\frac{?}{18}\)
مخرج بزرگتر را بر مخرج کوچکتر تقسیم کنید و سپس این نتیجه را در صورت کسر اول ضرب کنید:
\(18 \div 3=6\\
6 \cdot 2=12\)
\(\frac{4}{9}=\frac{24}{54}\)
\(\frac{4}{9}=\frac{?}{54}\\
54 \div 9=6\\
6 \cdot 4=24\)
\(\frac{12}{60}=\frac{1}{5}\)
\(\frac{45}{75}=\frac{3}{5}\)
\(\frac{135}{180}=\frac{3}{4}\)
\(\frac{108}{217}=\frac{108}{217}\)
اگر صورت و مخرج کسر شما اینقدر بزرگ باشند، با استفاده از روش رسمی آنها را کاهش دهید. ابتدا، هم صورت و هم مخرج کسر را به فاکتورهای اولشان تجزیه کنید:
\(\frac{108}{217}=\frac{(2 \cdot 2 \cdot 3 \cdot 3 \cdot 3)}{(7 \cdot 31)}\)
صورت و مخرج این کسر هیچ فاکتور مشترکی ندارند، بنابراین این کسر در حال حاضر در پایین ترین جملات ممکنش قرار دارد.
\(\frac{2}{9}\) بزرگتر از \(\frac{1}{5}\) است.
ابتدا این دو کسر را طرفین وسطین (Cross-multiply) کنید:

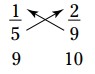
اکنون مخرج ها را در یکدیگر ضرب کنید تا مخرج مشترکی بیابید:
\(\frac{9}{45} \text{ ? } \frac{10}{45}\)
از آنجا که \(\frac{10}{45}\) بزرگتر از \(\frac{9}{45}\) است، پس \(\frac{2}{9}\) بزرگتر از \(\frac{1}{5}\) است.
\(\frac{3}{7} \gt \frac{5}{12} \)
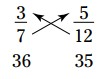
\(\frac{3}{29}\) از \(\frac{1}{10}\) و \(\frac{2}{21}\) بزرگتر است.
برای اینکه بین چند کسر بزرگترین یا کوچکترین را بدست آورید ابتدا آنها را دو به دو مقایسه کنید و سپس کسر بزرگتر با کوچکتر را بسته به درخواست مسأله، با کسر سوم مقایسه کنید، همین فرآیند را تا رسیدن به آخرین کسر تکرار کنید.
\(\frac{2}{7}\) کوچکتر از \(\frac{1}{3}\)، \(\frac{4}{13}\)، و \(\frac{8}{25}\) است.